Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Problemas - Ex. 54
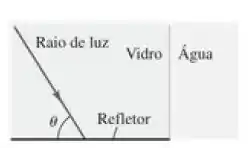
Um grande cubo de vidro possui um refletor de metal em uma das faces e água na face adjacente (Figura 33.52). Um feixe de luz incide sobre o refletor, como mostrado na figura. Você observa que, à medida que aumenta o ângulo do feixe de luz, se nenhuma luz pode entrar na água. Qual é a velocidade na luz nesse vidro?
Passo 1
Como o enunciado disse, se nenhuma luz pode entrar na água. Isso significa que . Nessa situação teremos reflexão interna total.
Então, vamos aplicar a lei de snell nessa configuração:
Então:
Mas calma que ainda não acabou. Queremos saber a velocidade da luz no vidro!
Passo 2
Para encontrarmos a velocidade, vamos usar a relação:
Então:
Fechou!!
Resposta
Exercícios de Livros Relacionados
Um feixe de luz está se propagando dentro de um cubo sólido de vidro com índice de refração 1,53 . O feixe atinge a superficie do cubo a partir de dentro. a) Se o cubo está no ar, com que ângulo mínim
A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a 1.60 . A luz desloca-se paralelamente à parte superior do tubo (Figura 33.40). Você deseja cortar a face A B
Um raio de luz proveniente do interior do diamante (índice refração 2.42 ) incide sobre sua interface com o ar. Qual é o maior ângulo que o raio pode formar com a normal para que ele não seja totalmen
Um raio de luz está se propagando em um cubo de vidro que está completamente imerso na água. Você descobre que, se o raio incide sobre a interface vidro-água em um ângulo maior do que 48 , 7 ° com a n
A luz incide na direção da normal na face A B de um prisma de vidro de índice de refração 1,52 , como mostra a Figura 33.41. Encontre o maior valor que o ângulo α pode ter para que nenhu- ma luz seja