Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 37

Voce esta parado na borda de uma piscina e olhando di-

retamente para o lado oposto.Voce nota que o fundo do lado opos-

to da piscina parece estar a um angulo de 28 abaixo da horizontal.

Entretanto,quando voce senta na borda da piscina,o fundo do lado

oposto parece estar a um angulo de apenas 14abaixo da horizontal.

Use estas observacoes para determinar a largura e a profundidade

da piscina.Dica:Voce precisara estimar a altura de seus ollios acima da

superficie da digun quando estiver em pe e sentado.

Passo 1

Os diagramas a seguir representam as situações quando você está de pé na beira da piscina (o diagrama à esquerda) e quando você está sentado na beira da piscina (o diagrama à direita). Podemos usar a lei de Snell e a geometria da piscina para determinar a largura e a profundidade da piscina.

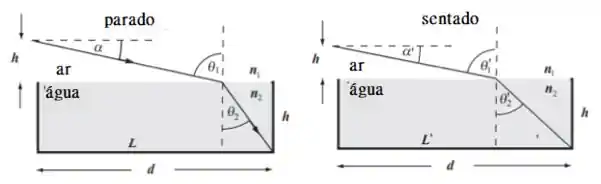
Use o fato de que os ângulos α e θ 1 são complementares, assim como α ' e θ 1 ' para determinar θ 1 e θ 1 '   :

θ 1 = 90 ∘ - α = 90 ∘ - 28 ∘ = 62 ∘   e   θ 1 ' = 90 ∘ - α ' = 90 ∘ - 14 ∘ = 76 ∘

Expresse as distâncias L e L ' em termos de θ 1 e θ 1 ' :

L = h em pé  t a n ⁡ θ 1   e   L ' = h s e n t a d o t a n ⁡ θ 1 '

Passo 2

Supondo que seus olhos estejam 1.7 m acima do nível da água quando você está de pé e 0.7 m acima da água quando você está sentado, avalie L e L ' :

L = ( 1.7 m ) t a n ⁡ 62 ∘ = 3.197 m   e   L ' = ( 0.7 m ) t a n ⁡ 76 ∘ = 2.808 m

então,

t a n ⁡ θ 2 = l h = d - L h                       ( 1 )   e   t a n ⁡ θ 2 ' = l ' h = d - L ' h

tan ⁡ θ 2 tan ⁡ θ 2 ' = d - L d - L ' d = L ' tan ⁡ θ 2 - Ltan ⁡ θ 2 ' tan ⁡ θ 2 - tan ⁡ θ 2 '                     ( 2 )

Aplique a lei de Snell à interface ar-água quando você estiver de pé:

θ 2 = s i n - 1 ⁡ n 1 n 2 sin ⁡ θ 1 θ 2 = s i n - 1 ⁡ 1.00 1.33 s i n ⁡ 62 ∘ = 41.60 ∘

Aplique a lei de Snell à interface ar-água quando você estiver sentado:

θ 2 ' = s i n - 1 ⁡ n 1 n 2 sin ⁡ θ 1 ' θ 2 ' = s i n - 1 ⁡ 1.00 1.33 s i n ⁡ 76 ∘ = 46.85 ∘

Passo 3

Substitua os valores numéricos na equação (2) e avalie d:

d = 2.808 m tan ⁡ 41.60 ∘ - 3.197 m tan ⁡ 46.85 ∘ tan ⁡ 41.60 ∘ - tan ⁡ 46.85 ∘ = 5.130 m = 5.1

Então, h será

h = d - L tan ⁡ θ 2 h = 5.130 m - 3.197 m tan ⁡ 41.60 ∘ = 2.2 m

Resposta

2.2m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bastão de vidro muito longo com 1,75c m de diâmetro tem um lado polido formando uma superfície esférica côncava com 7,20c m de raio. O material do vidro tem índice de refração de 1,68 . (a) Um obje
Um bastão de vidro muito longo com 1,75c m de diâmetro tem um lado polido formando uma superfície esférica convexa com 7,20c m de raio. O material do vidro tem índice de refração de 1,68 . (a) Um obje
Um bastão tem 96,0 cm de comprimento e é feito de vidro com índice de refração igual a 1,60. O bastão tem suas extremidades polidas formando superfícies esféricas convexas com raios iguais a 8,00 cm e
Um peixe está a 10c m da superfície da frente de um aquário esférico com 20c m de raio. (a) A que distância atrás da superfície do aquário o peixe parece está para alguém que o observe pela frente do
Na Figura 31-56,luz esta inicialmente em um meio quetem indice de refracao n,.Ela esta incidindo em um angulo 0,na su-perficie de um liquido que tem um indice de refracao n,.A luz passaatraves do liqu