Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 9
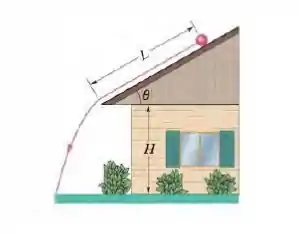
A figura abaixo um cilindro maciço com de raio e uma massa de parte do repouso e rola para baixo uma distância , sem deslizar, em um telhado com uma inclinação .
Qual é a velocidade angular do ciclindro em relação ao eixo central ao deixar o telhado?
A borda do telhado está a uma altura . A que distância horizontal da borda do telhado o cilindro atinge o chão?
Passo 1
Olá pessoal, tudo bem? Vamos praticar um pouco de dinâmica de rotação?
Para calcular a velocidade angular precisamos saber a aceleração angular (e pra ela a celeração do centro de massa ). Vamos começar com a aceleração do centro de massa:
Tal que:
Agora a aceleração angular será dada como:
Pronto! Agora podemos determinar a velocidade angular, sabendo que o cilindro partiu do repouso e percorreu temos:
De modo que:
Passo 2
Sabendo a velocidade angular, podemos calcular a velocidade linear do centro de massa:
E a componente vertical vai ser:
Enquanto que a componente horizontal vai ser:
Primeiro vamos determinar o tempo de queda, assim poderemos calcular depois o alcance horizontal.
Da equação horária da posição de um movimento vertical temos:
A posição final é no chão, então , daí substituindo os valores temos:
Pela fórmula de Bháskara (sim, ela voltou!) temos:
Apenas a raiz positiva é válida, sendo assim:
Passo 3
Agora podemos calcular o alcance!
Da fórnula da equação horária do momento na horizontal:
Como o tempo para o cilindro cair é o mesmo para ele se deslocar horizontalmente e como ele não tem aceleração na horizontal, ficou tranquilo de resolver: é só susbtituir