Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 76

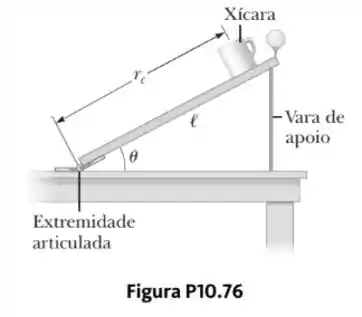
Uma demonstração comum, ilustrada na Figura P10.76, consiste em uma bola repousando em uma extremidade de uma mesa uniforme de comprimento l que é presa na outra extremidade e elevada a um ângulo de θ . Uma xícara leve está presa à mesa em r c para pegar a bola quando a vareta de apoio é removida subitamente.

  1. Mostre que a bola vai ficar para trás da mesa em queda quando θ for menor que 35,3 ° .
  2. Supondo que a mesa tenha 1,00   m de comprimento e seja suportada neste ângulo limitante, mostre que a xícara deve estar a 18,4   c m distante da extremidade que se move.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

O centro de gravidade da mesa uniforme está em seu meio. Para a mesa apenas começando a se mover,

∑ τ = I α :

m g l 2 cos ⁡ θ = 1 3 m l 2 α

α = 3 2 g l cos ⁡ θ

A aceleração tangencial do fim é a t = l α = 3 2 gcos ⁡ θ , e a sua componente vertical a y = a t cos ⁡ θ = 3 2 g cos 2 ⁡ θ .

Se for maior que g, o tabuleiro avançará à frente da bola em queda.

Passo 2

Letra a:

3 2 g cos 2 ⁡ θ ≥ g

cos 2 ⁡ θ ≥ 2 3

cos ⁡ θ ≥ 2 3

θ ≤ 35.3 ∘

Passo 3

Letra b:

Quando θ = 35.3 ∘ o copo vai pousar sob o ponto de liberação da bola se r c = l c o s ⁡ θ .

Quando l = 1.00 m   e   θ = 35.3 ∘ ,

r c = 1.00 m 2 3 = 0.816 m

Então o copo deveria estar a l - r c = 1.00 m - 0.816 m = 0.184 m da extremidade móvel.

Resposta

  1. θ ≤ 35.3 ∘
  2. Então o copo deveria estar a l - r c = 1.00 m - 0.816 m = 0.184 m da extremidade móvel.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força F → = - 8 N i → + 6 N j → age sobre uma partícula cujo vetor posição é r → = 3 m i → + 4 m j → . Qual é ( a ) o torque em relação à origem a que está submetida a partícula, em termos dos vetor
Em termos dos vetores unitários, qual é o torque em relação à origem a que está submetida uma partícula localizada nas coordenadas ( 0 ; - 4 m ; 3 m ) se esse torque se deve ( a ) uma força F 1 → de c
Uma ameixa está localizada nas coordenadas ( - 2 m ; 0 ; 4 m ) . Em termos dos vetores unitários, qual é o torque que se deve a uma força cuja única componente é a F x = 6 N , b F x = - 6 N , c F z =
Em termos dos vetores unitários, qual é o torque resultante em relação à origem que está submetida uma pulga localizada nas coordenadas 0 ; - 4 m ; 5 m quando as forças F 1 → = 3 N k → e F 2 → = - 2 N
Uma força F → = 2 N i → - 3 N k → age sobre uma pedra cujo vetor posição é r → = 0,5 m j → - 2 m k → , em relação à origem. Em termos do vetores unitários, qual é o torque resultante a que a pedra est