Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 56
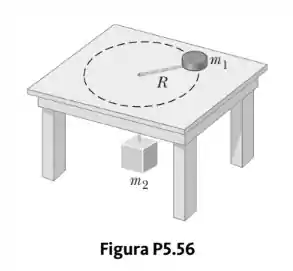
Um disco de massa é amarrado a um barbante e girado em um círculo de raio em uma mesa horizontal e sem atrito. A outra ponta do barbante passa por um pequeno furo no centro da mesa e um corpo de massa é amarrado a ele (Fig. P5.56). O corpo suspenso permanece em equilíbrio enquanto o disco gira sobre a mesa. Encontre as expressões simbólicas para
- a tensão no barbante,
- a força radial que atua sobre o disco e
- a velocidade do disco.
- Descreva qualitativamente o que acontecerá com o movimento do disco se o valor de for aumentado pela colocação de uma pequena carga adicional.
- Descreva qualitativamente o que acontecerá com o movimento do disco se o valor de for diminuído pela remoção de uma parte da carga pendurada.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Letra a:
Uma vez que o objeto de massa está em equilíbrio,
Passo 2
Letra b:
A tensão na corda fornece a aceleração centrípeta necessária do disco. Então:
Passo 3
Letra c:
De , temos:
Passo 4
Letra d:
O disco irá espiralar para dentro, ganhando velocidade à medida que o faz. Ele ganha velocidade porque a tensão da corda puxa em um ângulo de menos de 90 ° para a direção da velocidade de espiral para dentro, produzindo aceleração tangencial para frente, bem como para uma aceleração radial para dentro do disco.
Passo 5
Letra e:
O disco vai espiralar para fora, diminuindo a velocidade.
Resposta
- O disco irá espiralar para dentro, ganhando velocidade à medida que o faz. Ele ganha velocidade porque a tensão da corda puxa em um ângulo de menos de 90 ° para a direção da velocidade de espiral para dentro, produzindo aceleração tangencial para frente, bem como para uma aceleração radial para dentro do disco.
- O disco vai espiralar para fora, diminuindo a velocidade.