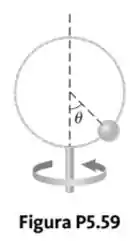
Uma única conta com atrito desprezível em um fio retesado foi curvada em um loop circular de raio , como mostrado na Figura P5.59. O círculo sempre está em um plano vertical e gira regularmente sobre seu diâmetro vertical com um período de . A posição da conta é descrita pelo ângulo q que a linha radial, do centro do loop até a conta, faz com a vertical.

1. Em que ângulo acima da parte inferior do círculo a conta pode ficar sem movimento com relação ao círculo girando?
2. E se? Repita o problema, desta vez considerando o período da rotação do círculo como .
3. Descreva como a solução para a parte (b) é diferente daquela para a parte (a).
4. Para qualquer período ou tamanho de loop há sempre um ângulo no qual a conta pode ficar imóvel em relação ao loop?
5. Há mais de dois ângulos em algum momento? Arnold Arons deu a ideia para este problema.

Então se torna:

Temos duas soluções:

E

Se a segunda solução nos dá:

Assim, neste caso, a conta pode andar em duas posições:

Letra b:

Nesta rotação mais lenta, a solução [2] acima torna-se:

Que é impossível.

Letra c:

Existe apenas uma solução para (b) porque o período é muito grande.

Letra d:

A equação que o ângulo deve satisfazer tem duas soluções sempre que , mas apenas a solução 0° caso contrário. A rotação do loop deve ser mais rápida do que um certo valor limite para que a conta se afaste da posição mais baixa. Zero é sempre uma solução para o ângulo.

Letra e:

A partir da derivação da solução em (a), nunca há mais do que duas soluções.