Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.5 - Ex. 51
Um bonde antigo dobra urna esquina fazendo uma curva plana com de raio a . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?
Passo 1
Oláaaa, querido! Cê tá bem?
Então, a alça de mão está dentro do bonde, certo? Quando o bonde faz a curva, ele tem aceleração centrípeta, que o mantém na rota de trajetória circular. Essa aceleração centrípeta tem essa fórmulinha:
Mas como a alça está presa no bonde, ela precisa ganhar essa aceleração também para se manter dentro do bonde. E que faz esse papel de “transmitir” a aceleração do bonde para a alça é a cordinha que prende a alça, ela aplica na alça uma tensão que a mantém na trajetória circular também.
Então, se a gente for fazer um diagrama de corpo livre da situação, vamos ter:
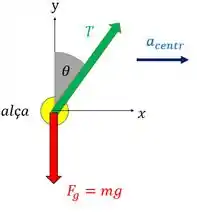
Percebe que essa tensão na corda é inclinada porque uma parte dela causa a aceleração na alça e a outra parte manté a alça presa no teto se opondo a força peso.
E por isso, a corda (responsável pela força ), faz um ângulo com a vertical. Ele quer saber esse ângulo. Como fizemos um diagrama de corpo livre, nada mais justo que usar a segunda lei de Newton para resolver essa. Bora lá!
Passo 2
Aplicando a segunda lei de Newton para a direção :
Nessa direção a gente tem a aceleração centrípeta que vale :
E nessa direção só temos a componente da tensão na cordinha. Como o ângulo está oposto ao eixo , essa componente vale . Substituindo:
Passo 3
E agora vamos aplicar a segunda lei de Newton para a direção . Nela não há aceleração, porque não tem movimento nessa direção. Então temos
E nessa direção a gente tem a força peso e componente de que vale , se oponto, logo elas tem sinais inversos. Substituindo na nossa equação:
Substituindo as expressões de cada uma
Passo 4
Temos duas equações:
Dividindo a primeira equação pela segunda, temos que:
Substituindo os dados do problema, lembrando de passar a velocidade para dividindo ela por :
Resposta
Tranquilo galera??? Bora resolver mais questões então!!!!!!!