Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 37
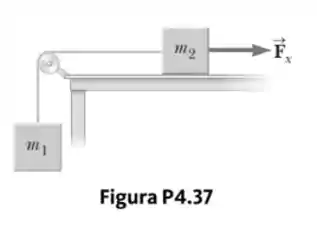
No sistema mostrado na Figura P4.37, uma força horizontal age sobre um corpo de massa . A superfície horizontal não tem atrito. Considere a aceleração do corpo deslizando em função de .
- Para quais valores de o corpo de massa acelera para cima?
- Para quais valores de a tensão na corda é zero?
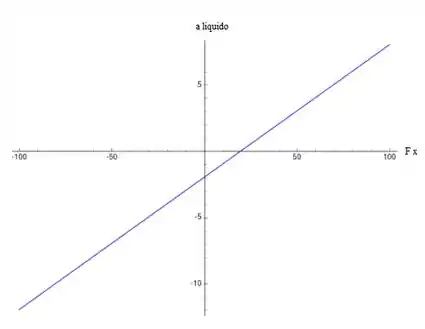
- Faça um gráfico da aceleração do corpo por . Inclua os valores de de a .
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Letra a:
Temos:
Então, a aceleração é:
Então a massa acelera pra cima para
Passo 2
Letra b:
A tensão da corda é dada por:
Consequentemente, para , a tensão da corda será zero. Aqui o sinal negativo significa a força a ser aplicada na direção oposta.
Passo 3
Letra c:
A aceleração do sistema é dada por:
Usando a equação acima, podemos plotar a aceleração como uma função de . O gráfico é mostrado abaixo.
Resposta
Exercícios de Livros Relacionados
Na situação descrita no Problema 45 e mostrada na Figura P4.45, as massas da corda, balança de mola e polia são desprezíveis. Os pés de Nick não estão tocando o chão. Suponha que Nick esteja momentane
Na máquina de Atwood discutida no Exemplo 4.4 e mostrada na Figura Ativa 4.12a, m 1=2,00k g e m 2=7,00k g . Por comparação, as massas da polia e da corda são desprezíveis. A polia gira sem atrito e a
Uma criança inventiva chamada Nick quer pegar uma maçã em uma árvore sem escalá-la. Sentado em uma cadeira conectada a uma corda que passa sobre uma polia sem atrito (Fig. P4.45), Nick puxa a ponta so
Inicialmente, o sistema dos corpos mostrados na Figura P4.51 é mantido sem movimento. A polia e todas as superfícies não têm atrito. Seja a força F → zero e assuma que m 1 pode se mover apenas vertica
Três corpos estão conectados sobre uma mesa, como mostrado na Figura P5.14. O coeficiente de atrito cinético entre o bloco de massa m 2 e a mesa é 0,350 . Os corpos têm massa de m 1=4,00k g , m 2= 1,0