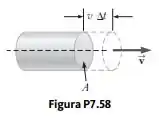
Uma máquina empurra uma quantidade crescente de neve na sua frente à medida que percorre um estacionamento. Suponha que um carro que se move pelo ar seja modelado como um cilindro de área A, empurrando um disco de ar que fica maior à sua frente. O ar, originalmente estacionário, é colocado em movimento com uma velocidade constante do cilindro, como mostrado na Figura P7.58. Em um intervalo de tempo , um novo disco de ar de massa deve ser movido por uma distância e, portanto, lhe é dada uma energia cinética . Usando esse modelo, mostre que a perda de potência do carro por causa da resistência do ar é e que a força resistiva que atua sobre o carro é , em que é a densidade do ar. Compare esse resultado com a expressão empírica para a força resistiva.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
A densidade é:
Passo 2
Substituindo isso na primeira equação e resolvendo P, uma vez que para uma velocidade constante, temos:
Uma vez que , também temos:
Nosso modelo prevê as mesmas proporcionalidades que a equação do modelo empírico e nos dá para o coeficiente de arrasto. O ar na verdade desliza ao redor do objeto em movimento em vez de se acumular na frente dele. Por esta razão, o coeficiente de arrasto não é necessariamente unitário.
Normalmente é menos de um para um objeto simplificado e pode ser maior que um se o fluxo de ar ao redor do objeto for complicado.
Resposta
Ver solução