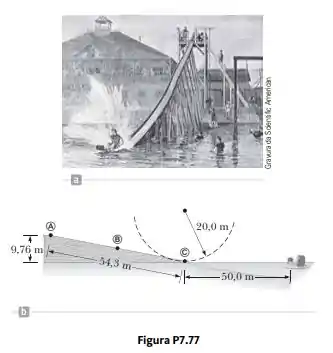
Em 1887, em Bridgeport, Connecticut, C. J. Belknap construiu um tobogã aquático mostrado na Figura P7.77. Um passageiro em um pequeno trenó, de massa total de , empurrou-se para começar no topo do escorregador (ponto A) com velocidade de . A rampa tinha de altura e de comprimento. Ao longo do seu comprimento, pequenas rodas tornaram o atrito desprezível. Ao deixar a rampa horizontalmente de sua base (ponto C), o passageiro deslizou pela água de Long Island Sound por até , “deslizando como uma pedra chata” antes de finalmente chegar ao repouso e nadar para a margem, puxando seu trenó com ele. (a) Encontre a velocidade do trenó e do passageiro no ponto C. (b) Modele a força de atrito da água como uma força de retardo constante atuando sobre uma partícula. Encontre o módulo da força de atrito que a água exerce sobre o trenó. (c) Encontre o módulo da força que a rampa exerce sobre o trenó no ponto B. (d) No ponto C, a rampa é horizontal, mas curva-se no plano vertical. Suponha que seu raio de curvatura seja . Encontre a força que a rampa exerce sobre o trenó no ponto C.

Letra b:

Incorporando a perda de energia mecânica durante a porção do movimento na água, temos, para todo o movimento entre A e D (o ponto de parada do passageiro):

A água exerce uma força de fricção (atrito):

e também uma força normal de:

A magnitude da força da água é:

Letra c:

O ângulo do trenó é:

Para forças perpendiculares à pista em B temos que

Letra d:

Para