Materiais Magnéticos
Teoria
Introdução
Lá na eletrostática, o meio que estávamos analisando algum fenômeno influenciava diretamente na magnitude do campo elétrico, alterando a permissividade do meio .
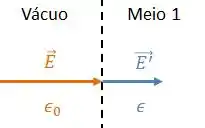
Aqui no magnetismo temos a mesma dependência do meio.
Lembra da Lei de Biot-Savart? Ela nos dá o campo magnético pela seguinte expressão:
Esse , chamado de permeabilidade magnética do meio, pode ser diferente dependendo do meio.
Por exemplo: se aproximarmos um fio que conduz uma corrente de um placa de ferro, o campo magnético medido no interior desta placa será diferente do campo no vácuo, para uma mesma distância.
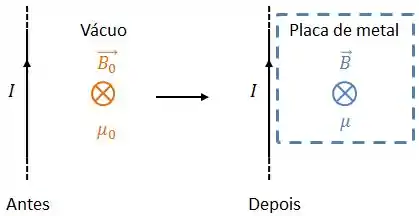
Mas como trabalhamos com esse ?
Moleza! O problema normalmente vai te dar a permeabilidade relativa do meio , que respeita a seguinte relação:
Onde:
Outra relação que podemos usar é a que equaciona a permeabilidade relativa com a suscetibilidade magnética do meio :
Portanto, podemos montar uma relação final:
Em relação aos valores de , podemos concluir algumas coisas:
- Se , o material é diamagnético. São materiais que não possuem momento magnético permanente e nem podem ser imantados.
- Se , o material pode ser paramagnético ou ferro magnético
- Se for positivo porém pequeno então o material será paramagnético: são materiais que não possuem momento magnético permanente mas que podem ser imantados um pouquinho caso estejam em um campo magnético forte.
- Se for positivo e grande, temos o ferromagnetismo: são materiais que podem se tornam permanentemente imãs caso estejam em presença de campo magnético, respondendo fortemente a esse campo.
Tranquilo? Nenhum bicho de 7 cabeças né? Mas não deixe de praticar!
Mas como trabalhamos com esse μ ?
Exercícios Resolvidos
Exercício Resolvido #1
USP-P2-2015-3
A figura abaixo mostra uma bobina toroidal com espiras bem compactadas. Uma corrente percorre o enrolamento desta bobina.
Calcule o módulo do campo magnético em um ponto no interior da bobina, a uma distância do seu eixo, quando a bobina é constituída só pelo enrolamento (núcleo de ar). Lembre que para o magnetismo o ar é praticamente indistinguível do vácuo.
Calcule a relação entre as correntes e na bobina com núcleo de ar e com núcleo de ferro , respectivamente que produzem o mesmo campo magnético no ponto .
Calcule a suscetibilidade do alumínio se com o núcleo de alumínio e mesma corrente o campo magnético no ponto passa a ser do valor no ar. Como se designa esse elemento segundo sua propriedade magnética?
Passo 1
Calcule o módulo do campo magnético em um ponto no interior da bobina, a uma distância do seu eixo, quando a bobina é constituída só pelo enrolamento (núcleo de ar). Lembre que para o magnetismo o ar é praticamente indistinguível do vácuo.
Pra calcular o campo magnético, vamos recorrer à Lei de Ampère, dada por:
Dada a simetria do problema, a nossa curva será a circunferência de raio por onde passa a bobina.
Além disso, como estamos falando que uma bobina de espiras por onde passa uma corrente , podemos dizer que .
Então podemos simplificar a Lei de Ampère dessa forma:
Passo 2
Calcule a relação entre as correntes e na bobina com núcleo de ar e com núcleo de ferro , respectivamente que produzem o mesmo campo magnético no ponto .
Quando colocamos um material magnético, o campo magnético é multiplicado pelo valor de . Assim, o campo magnético para o ferro será:
E para o ar, como :
O que queremos descobrir aqui é a relação entre e para que os campos magnéticos sejam iguais. Logo:
Simplificando esse cara de cima:
Passo 3
Calcule a suscetibilidade do alumínio se com o núcleo de alumínio e mesma corrente o campo magnético no ponto passa a ser do valor no ar. Como se designa esse elemento segundo sua propriedade magnética?
Opa! Então agora o que o problema está dizendo é que:
Logo:
Simplificando esse cara:
A relação entre e a suscetibilidade é dada por:
Logo, o alumínio é paramagnético.
Resposta
O alumínio é paramagnético.
Exercício Resolvido #2
USP-P3-2012-1
Um solenoide longo, com enrolamento compacto, produz um campo magnético em seu interior, no vácuo.
Quando o solenoide é preenchido por um determinado material, observa-se que o campo magnético no seu interior diminui para . Calcule a susceptibilidade magnética do material. Como se classifica esse material quanto à sua propriedade magnética?
O solenoide é agora preenchido por um núcleo de ferro com permeabilidade magnética 1000 vezes maior que o valor no vácuo. Determine a magnetização e o campo magnético no interior do núcleo em função de e .
Quando a corrente no solenoide é desligada, o núcleo de ferro apresenta uma magnetização remanente uniforme igual a . Determine o novo valor do campo magnético no interior do núcleo.
Passo 1
Quando o solenoide é preenchido por um determinado material, observa-se que o campo magnético no seu interior diminui para . Calcule a susceptibilidade magnética do material. Como se classifica esse material quanto à sua propriedade magnética?
A susceptibilidade magnética está associada à permeabilidade magnética por:
Como é diretamente proporcional a e é diretamente proporcional a , podemos dizer que:
Portanto:
Finalmente:
Como , o material é diamagnético.
Passo 2
O solenoide é agora preenchido por um núcleo de ferro com permeabilidade magnética 1000 vezes maior que o valor no vácuo. Determine a magnetização e o campo magnético no interior do núcleo em função de e .
A permeabilidade magnética está é dada por:
Assim como anteriormente, como é proporcional a e é proporcional a , podemos dizer que:
Passo 3
A magnetização está associada aos campos e por:
Sabendo agora que , substituindo na expressão acima, teremos:
Finalmente:
Passo 4
Quando a corrente no solenoide é desligada, o núcleo de ferro apresenta uma magnetização remanente uniforme igual a . Determine o novo valor do campo magnético no interior do núcleo.
A magnetização está associada aos campos e por:
Quando a corrente no solenoide é desligada, . Portanto:
Resposta
Como , o material é diamagnético.
Exercício Resolvido #3
Sears & Zemanske, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12ª ed., São Paulo: Addison Wesley, 2009, Problema 28.46, pp. 274
Um solenoide toroidal com 400 espiras possui um raio médio igual a 6,0 cm e conduz uma corrente de 0,25 A. A permeabilidade relativa do núcleo é igual a 80. (a) Qual é o campo magnético no núcleo? (b) Que parte do campo magnético resultante é produzido pelas correntes atômicas?
Passo 1
Bom, o problema deu a permeabilidade relativa do núcleo:
Lembrando que
Passo 2
Para resolver a letra (a) precisamos da fórmula do campo magnético em um toróide:
Sendo o número de espiras, a corrente e o raio do toróide.
Passo 3
Para resolver a letra (b) precisamos saber que a contribuição das correntes atômicas é dada pela diferença entre calculado com e calculado com .
Vamos calcular B sem considerar o material magnético (vou chamar de B’ para não haver confusão):
Assim:
Como queremos a parte do campo magnético resultante que é produzido pelas correntes atômicas, temos:
Podemos reparar que o material magnético inserido no toroide aumenta consideravelmente o campo magnético, sendo responsável por deste.
Resposta
(a)
(b)
Exercício Resolvido #4
Sears & Zemanske, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12ª ed., São Paulo: Addison Wesley, 2009, Problema 28.47, pp. 274
Um solenoide toroidal com 500 espiras é constituído por um enrolamento sobre um anel cujo raio médio é igual a 2,90 cm. Calcule qual deve ser a corrente no enrolamento necessária para produzir um campo magnético de 0,350 T no anel, (a) supondo que o anel seja de ferro recozido (); (b) supondo que o anel seja de aço com silício ()
Passo 1
Bom, o problema deu a permeabilidade relativa do anel:
Lembrando que
Para resolver a questão precisamos da fórmula do campo magnético em um toróide:
Sendo o número de espiras, a corrente e o raio do toróide.
Como o problema quer a corrente no toróide em casa caso, vamos explicitar a corrente i na fórmula acima:
Passo 2
Para a letra (a), temos que
Então:
E:
Passo 3
Para a letra (b), temos que
Então:
E:
Obs.: Se o toróide estivesse preenchido apenas com ar, precisaríamos de uma corrente muito maior para produzir o mesmo campo magnético. Essa é a vantagem de utilizar materiais magnéticos!
Resposta
(a)
(b)
Exercício Resolvido #5
Sears & Zemanske, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12ª ed., São Paulo: Addison Wesley, 2009, Problema 28.48, pp. 274
A corrente que passa nos enrolamentos de um solenoide toroidal é de 2,400 A. Existem 500 espiras e seu raio médio é igual a 25,0 cm. O toróide está preenchido com um material magnético. Verifica-se que o campo magnético no interior das espiras é igual a 1,940 T. Calcule (a) a permeabilidade relativa; (b) a suscetibilidade magnética do material que preenche o toróide.
Passo 1
Para resolver a questão precisamos da fórmula do campo magnético em um toróide:
Passo 2
Na letra (a), precisamos encontrar . Vamos rearrumar a fórmula do passo anterior:
Substituindo, temos:
Passo 3
Na letra (b) precisamos lembrar a fórmula da suscetibilidade magnética:
Portanto:
Substituindo:
Resposta
(a)
(b)