Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.6 - Ex. 56a

A figura 29-72a mostra um fio que conduz uma corrente i e forma uma bobina circular com apenas uma espira. Na figura 29-72b, um fio de mesmo comprimento forma uma bobina circular com duas espiras de raio igual à metada do raio da espira da figura 29-72a. (a) Se B a e B b são os módulos dos campos magnéticos nos centros das duas bobinas, qual é o valor da razão B b / B a ?

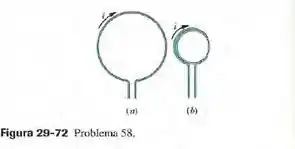
Passo 1

Fala aí! tudo certinho? 😉

Nesse problema temos duas espiras que são percorridas por uma corrente i sendo que uma espira tem raio r e outra tem raio r / 2 e duas espiras.

A partir daí queremos saber qual é a razão B b / B a dos campos magnéticos das espiras.

Tem ideia de como fazer isso? 🤔

Bom, lá da teoria de campos magnéticos produzidos por correntes, temos a situação de um campo produzido no centro de uma circunferência, lembra? Lá a gente encontra a seguinte fórmula para calcular o campo:

B = μ o i 2 R

E portanto, B ∝ i / R .

Bora começar! 😉

Passo 2

Na nossa questão, queremos encontrar a razão entre os campos magnéticos gerados pelas duas bobinas. Como a bobina b tem duas espiras, temos:

B b = 2 μ o i 2 R b ,     B a = μ o i 2 R a

Fazendo B b / B a , temos

B b B a = 2 μ o i 2 R b μ o i 2 R a = 2 i R b i R a

B b B a = 2 R a R b

Mas como R b = R a / 2 , temos

B b B a = 2 R a R a 2 = 4 R a R a

B b B a = 4,0

E aí! entendeu tudo? Responde Aí!

Resposta

A razão é igual a:

B b B a = 4,0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que, no interior de uma ímã permanente (Seç. 11.8), podemos introduzir para o campo H → um novo potencial escalar magnético ξ tal que H → = - ∇ ξ , onde ξ está relacionado com a magnetização M
No problema anterior, a área da secção reta do anel é de 1c m 2 . Calcule:a) a energia armazenada no interior do ferro;b) a energia armazenada no entreferro;c) a auto-indutância do sistema.
Verifica-se que a contribuição máxima da magnetização do ferro ao valor de B no material é da ordem de 2 T . A massa atômica do ferro é 55,8 e sua densidade é 7,9g / c m 3 . a) Se cada elétron contrib
Como aplicação do problema anterior, considere um ímã permanente em forma de barra cilíndrica de raio a e comprimento l ≫ a . Nessas condições, podemos admitir, como aproximação, que a barra está unif
Exercício de Livro