Teoria
Introdução
Batimento é um fenômeno que ocorre quando duas ondas com frequências diferentes, porém muito próximas chegam aos nossos ouvidos simultaneamente.
Por terem frequências muito próximas, as ondas irão se interferir construtivamente quando em fase e destrutivamente quando em oposição de fase.
O resultado disso é que ouviremos um som cuja intensidade se alterna entre alta e baixa, e é exatamente por isso que se chama Batimento.
Equacionando...
Vamos ver agora o que ocorre algebricamente com as equações de onda, lembrando que se tratam de ondas longitudinais. Por conta disso, iremos utilizar a notação .
Dadas então duas ondas com mesma amplitude e frequências distintas:
Por termos frequências distintas, temos frequências angulares distintas, pois , lembra?!
Somando as duas ondas, temos que a resultante fica:
Utilizando a seguinte identidade:
Temos:
Geralmente, definimos:
A onda resultante fica:
Podemos pensar nessa onda como uma onda cuja frequência angular é e cuja amplitude varia com . Essa onda fica com essa uma cara parecida com essa aqui:
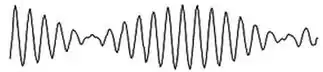
Podemos definir a frequência angular do batimento, , que será:
Como temos que , temos que a frequência de batimento será:
Show? Então, o principal daqui são as fórmulas da frequência e da frequência angular do batimento. Não esqueça delas nunca!
Equacionando...
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 51
A corda lá de um violino está esticada demais. São ouvidos batimentos por segundo quando a corda é tocada junto com um diapasão que oscila exatamente na frequência do lá de concerto (). Qual o período de oscilação da corda do violino?
Passo 1
O enunciado nos diz que a frequência de batimento que surge quando tocamos o violino e o diapasão ao mesmo tempo é de , certo?
Aprendemos que a frequência de batimento é obtida simplesmente pela subtração das duas frequências existentes. Mas como vamos saber nesse caso qual é a maior?
Bem, a primeira frase do enunciado diz que a corda está mais esticada do que deveria. Vamos lembrar duas fórmulas:
e
Juntando as duas:
O que tiramos daqui? Se aumentarmos a tração, aumentamos a frequência, beleza?
Então essa corda do violino esticada resulta em uma frequência maior do que a frequência do diapasão, portanto:
Substituindo os valores:
E agora é fácil obter o período:
Resposta
Exercício Resolvido #2
Ao se analisar as emissões vocais captadas no microfone do Silvio Santos, constatou-se que a onda gerada é composta pela superposição de ondas sonoras senoidais
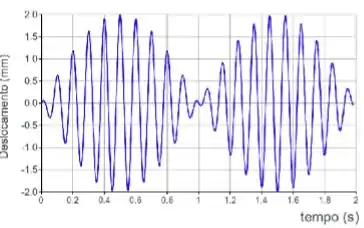
Com relação ao padrão de superposição gerado pelas ondas e , se observa que:
A onda resultante apresenta frequência média de e de batimento de
A onda estacionária descrita possui período de .
O gráfico descreve o batimento gerado.
O gráfico descreve a onda estacionária no harmônico.
O gráfico decorre do padrão de interferência construtiva gerado.
Passo 1

Ma oeee....Ma vamos entender o gráfico antes, que não vale barras de ouro, mas vale mais do que dinheiro: O gráfico mostra o deslocamento que a partícula tem em um determinado intervalo de tempo.
O gráfico apresentado é o tipo de gráfico que representa um batimento...por quê? Bem, porque o gráfico mostra dois momentos: um em que a oscilação é rápida (alta frequência) e outro momento em que ela é mais lenta baixa frequência. E essa é a situação típica de um batimento. Porque as frequências das ondas sobrepostas são diferentes. Então vamos marcar a alternativa por enquanto.
A alternativa diz que a frequência de batimento é . Isso está errado, porque a frequência de batimento é a frequência do trecho de oscilação lenta, que ocorre em e por isso a frequencia é .
Esse é o trecho de oscilação lenta, pois em um mesmo intervalo de tempo a distância percorrida pela onda é bem pequena se comparada com outros pontos.
As alternativas e pressupõem que a onda gerada é uma onda estacionária, o que só ocorreria se as frequências de oscilação da onde e fossem iguais e com os sentidos de propagação contrários entre si. No gráfico observamos exatamente o efeito contrário.
A alternativa , o padrão de interferência construtiva é aquele que amplifica todos os ventres e vales da onda, certo? Na figura não vemos isso ocorrendo, tem pontos que foi amplificado, mas também tem pontos que foi reduzido e pontos intermediários. Por isso que temos trechos de diferentes oscilações.
Então a única opção correta é a .

Resposta
Letra
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 52
Um diapasão de frequência desconhecida produz batimentos com um segundo diapasão-padrão com frequência de . A frequência de batimento diminui quando um pequeno pedaço de cera é colocado em um dos braços do primeiro diapasão. Qual é a frequência desse diapasão?
Passo 1
Se lembrarmos que a frequência de um oscilador massa mola é proporcional a , concluímos que a frequência do primeiro diapasão diminui quando o pedaço de cera é colocado, certo?
Mas o que isso tem a ver com a solução?
Isso nos ajuda a ver qual vai ser a ordem da subtração na fórmula da frequência de batimento, já que ela é positiva.
Para a frequência de batimento diminuir quando a frequência do primeiro diapasão diminuir, é necessário que:
Onde é a frequência do diapasão desconhecido.
Resposta
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 53
Duas cordas de piano iguais têm uma frequência fundamental de quando submetidas a uma mesma tensão. Que aumento relativo da tensão de uma das cordas faz com que haja batimentos por segundo quando as duas cordas oscilam simultaneamente?
Passo 1
Vamos lembrar aqui de duas fórmulas conhecidas da gente:
Se juntarmos as duas e isolarmos a frequência:
Vamos chamar as frequências das cordas de e . Como um aumento na tensão causará um aumento na frequência, se escolhermos a corda 1 para aumentarmos a tensão, temos:
Passo 2
Vamos chamar de a nova tensão aplicada na corda 1. Então:
Mas nós temos o valor de , que é:
Então, se multiplicarmos a expressão de por , temos:
Passo 3
Voltando agora na fórmula do batimento:
O aumento relativo é dado por:
Juntando as duas equações, temos:
Equacionando e elevando ao quadrado:
Resposta
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 54
Cinco diapasões oscilam com frequências próximas, mas diferentes. Quais são os números (a) máximo e (b) mínimo de frequências de batimento diferentes que podem ser produzidas tocando os diapasões aos pares, dependendo da diferença entre as frequências?
Passo 1
a) Lembrando lááá da análise combinatória, se temos um conjunto de 5 coisas e queremos escolher duas delas, qual fórmulas usamos?
Isso aí , então:
Teremos esse como valor máximo de frequências de batimentos.
Passo 2
b) O mínimo ocorrerá quando a diferença entre as frequências sucessivas forem iguais. Melhorando a explicação: imagina que as frequências são e , então, teríamos:
Onde varia de a e é um valor qualquer.
Nesse caso teríamos apenas 4 frequências de batimento: e .
Resposta
- frequências de batimento
- frequências de batimento