Interferência por Duas Fendas Pontuais
Teoria
O experimento de Young
O experimento de Young é o seguinte: você coloca um laser atrás de uma fenda, passando depois por dois buraquinhos bem pequenos, que vamos chamar de e e atingindo sua parede.
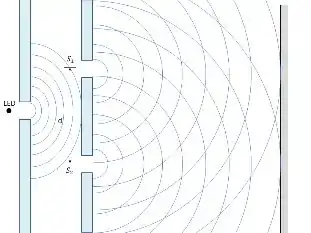
A imagem que você vai ver são franjas coloridas e escuras alternadas, algo parecido com isso:
Onde eu escolhi luz vermelha porque fica muito mais irado (prevejo flamenguistas curtindo... pior que sou vascaíno haha).
Onde vão estar as franjas brilhantes?
As fendas e agem como duas fontes luminosas cujas distâncias a diversos pontos do anteparo são diferentes, causando diferença de fase.
Olhe para a figura abaixo, onde a distância entre as fendas e a parede é muito maior que a distância entre as duas fendas .
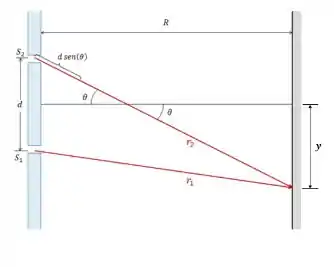
Como , podemos dizer que e são aproximadamente paralelas.
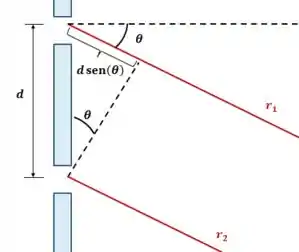
As duas ondas vão percorrer uma distância diferente, chegando na parede fora de fase. De acordo com a figura acima, essa diferença de caminho ótico vai ser dada por:
Os pontos de interferência construtiva e destrutiva são dados por
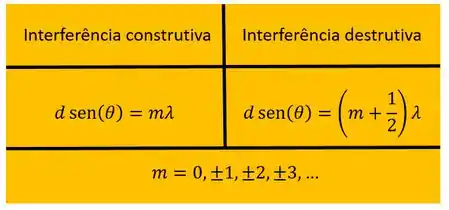
A figura na sua parede é formada pela alternância destes pontos de interferência construtiva e destrutiva. Chamamos essa imagem de Franjas de Interferência, representada abaixo.
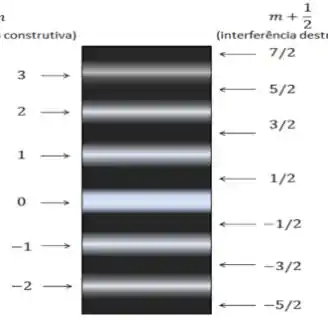
Existe um limite para o tamanho da nossa figura? Sim!
A medida que se aproxima de , a luz vai incidindo cada vez mais longe do centro, até que pra a luz não atingiria mais o anteparo! Então a última franja que aparece corresponde à .
Distância angular entre máximos e mínimos
E se vier uma questão na prova querendo a distância entre duas franjas de interferência?
Primeiro, vamos ficar calmos. O ângulo das franjas em relação à franja central é dado pelas condições de interferência construtiva e destrutiva (quadradinho amarelo lá em cima!)
Mas e o ângulo entre duas franjas quaisquer? Acontece que, para ângulos bem pequenos, podemos aproximar as funções trigonométricas.
;
Assim, para franjas claras e franjas escuras, temos:
E o ângulo entre duas franjas escuras ou duas franjas claras vai ser dado por:
Para máximos ou mínimos adjacentes, , e ambas as fórmulas se reduzem a:
“Que verdadeiro presente dos deuses! Quando poderei usufruir de tal presente?”
Bem, aí as vezes o exercício/prova/professor vai te dizer. Outras vezes, ninguém vai te dizer. Na dúvida, use sem medo, pois muitas vezes o exercício já considera que você vai usar.
Distância entre máximos e mínimos
Ok, a prova pode não pedir exatamente ângulos, e sim a diferença das alturas no anteparo. Vamos ver como podemos calcular ela.
A distância de uma franja para o centro pode ser encontrada usando a tangente do ângulo.
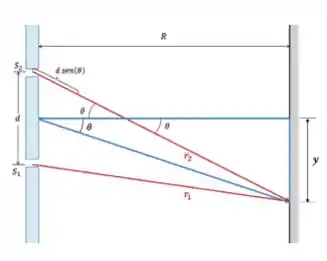
Como a gente considera os raios e são considerados paralelos. Se traçarmos uma linha reta paralela a e partindo do ponto médio de , teremos o triângulo azul acima.
Dele, podemos tirar que:
Porém, novamente nosso presente divino irá nos ajudar! Pois, para pequenos ângulos:
Substituindo nas condições de máximo, temos que:
Substituindo nas de mínimo, chegamos a:
Com isso, podemos calcular a distância entre 2 máximos ou 2 mínimos quaisquer subtraindo suas distâncias até o centro da figura.
Para máximos ou mínimos adjacentes, a fórmula vai ficar da seguinte forma:
Ou seja, a distância entre as franjas brilhantes e a distância entre as franjas escuras é aproximadamente constante.
O quão brilhante são as luzes que vejo lá ao longe?
Esse brilho que a gente vê em cada ponto da figura de interferência não é nada mais que o reflexo da intensidade do seu campo elétrico!
No meio de cada franja brilhante, sabemos que a interferência é construtiva. No meio de cada franja escura, sabemos que a interferência é destrutiva.
Mas de uma franja clara pra uma franja escura o brilho forma um degradê: ele vai variando aos poucos do claro pro escuro. Como saber o quão brilhante vai ser um ponto qualquer na minha parede?
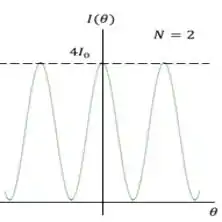
Como já falamos, esse brilho é a intensidade da luz. Ela varia continuamente ao longo da figura de interferência, formando um gráfico assim:
Em um ponto qualquer do anteparo, essa intensidade vai seguir a seguinte fórmula:
Onde:
- é a intensidade da luz incidente no sistema de dupla fenda.
- é a diferença de fase resultante da diferença de caminho ótico das duas ondas luminosas, dada por:
Note que nos pontos onde a intensidade é a maior possível (que são as nossas franjas brilhantes), ela é quatro vezes maior que a da luz incidente ().
Esses pontos correspondem a nossa condição de que .
Nesse caso, a diferença de fase vai ser um múltiplo inteiro de , fazendo o cosseno valer na nossa expressão (que é o maior valor possível).
Além disso, os pontos para a intensidade zero são aqueles nos quais é um múltiplo inteiro ímpar de , fazendo o coseno valer zero.
Para ângulos pequenos, e . Podemos reproduzir a discussão acima usando a distância dos pontos da figura em relação ao centro, ao invés do ângulo.
Onde é a distância das fendas ao anteparo. Substituindo na diferença de fase:
E isso é tudo, amigos!
Ah, só mais uma coisa!
Em alguns lugares, você pode encontrar a fórmula escrita dessa forma:
Neste caso, é a intensidade da franja brilhante central da figura de interferência!
A intensidade nesse ponto é , e aí as duas fórmulas são iguais.
O que acontece se colocarmos nosso brinquedo na água?
As suas provas ou listas de exercício podem querer apimentar um pouco a relação, e colocar todo o experimento de Young dentro da água (ou qualquer outro meio, tipo óleo, refrigerante, sei lá). Nesse caso, o que vai mudar?
Quando a luz se propaga em diferentes meios, ela assume velocidades diferentes. Ela é dada por:
Contudo ela permanece com a mesma frequência e por isso o comprimento de onda tem que variar com a velocidade.
O que mede o quanto a velocidade varia é o índice de refração do meio, que é dado pela razão entre a velocidade da luz no vácuo e a velocidade da luz naquele meio.
Vamos juntar as duas equações e ver como o comprimento de onda muda:
Isso significa que sempre que usarmos as condições de interferência, usaremos esse comprimento de onda , ao invés de como fazíamos antes.
E aí? Bastante coisa né? Por isso mesmo que tem um montão de exercício aqui pra você! Simbora o/
Distância angular entre máximos e mínimos
Distância entre máximos e mínimos
O quão brilhante são as luzes que vejo lá ao longe?
O que acontece se colocarmos nosso brinquedo na água?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 101-14, modificado.
Uma luz verde monocromática com um comprimento de onda de é usada para iluminar duas fendas estreitas paralelas separadas por uma distância de .
Calcule o desvio angular (ângulo ) da franja clara de terceira ordem () em graus.
Passo 1
Primeiro, vamos lembrar qual a condição para que a franja de interferência seja clara (ou seja, a interferência seja construtiva):
Porém, como queremos a de terceira ordem (), temos:
Passo 2
Agora, para achar , nós invertemos a equação:
Substituindo os valores dados pelo problema ( e ), temos que:
Agora, nós fazemos a inversa do seno:
Passo 3
Por fim, passando para graus com uma regrinha de 3, ficamos com:
Resposta
O desvio angular da franja clara de terceira ordem é de .
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 102-17, modificado
Um sistema de dupla fenda produz franjas de interferência para a luz do sódio ( ) com uma separação angular de . Para que comprimento de onda a separação angular é 10% maior?
Passo 1
Primeiro, vamos lembrar das condições de máximo para o sistema de dupla fenda.
Porém, como a separação angular é pequena, vamos usar a aproximação :
Com isso, a separação angular entre dois máximos adjacentes é dada por:
Passo 2
Seja o comprimento de onda que faz com que a separação angular seja 10% maior. Neste caso:
Cortando dos dois lados, ficamos com:
Resposta
O comprimento de onda que aumenta em 10% a separação angular nesse sistema de dupla fenda é .
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 102-20, modificado.
No experimento de dupla fenda da Fig.35-10, o ângulo é , a distância entre as fendas é e o comprimento de onda é .
- Que múltiplo de corresponde à diferença de fase entre as ondas associadas aos raios e ao chegarem ao ponto da tela distante?
- Qual é a diferença de fase em radianos?
- Determine a posição do ponto P, indicando o máximo ou mínimo em que se encontra ou o máximo e o mínimo entre os quais se encontra.
Passo 1
a)
Primeiro, lembremos que a diferença de fase entre as duas ondas se dá pela diferença de caminho. Assim, em múltiplos de , temos uma diferença de fase de:
Passo 2
Para o experimento de dupla fenda, sabemos que:
Logo, a diferença de fase vai ser:
Lembrando que , e que , a diferença de fase vai ser, em múltiplos de :
Passo 3
b)
Para acharmos a diferença de fase em radianos, vamos fazer o seguinte raciocínio.
Quando a diferença de fase de duas ondas é , isso equivale a uma diferença de fases de .
Logo, a diferença de fase em radianos vai ser a diferença de fases em múltiplos de multiplicado por
Passo 4
c)
Para achar a posição do ponto , temos que nos lembrar do seguinte:
Interferência construtiva se dá quando a diferença de fase é um múltiplo inteiro do comprimento de onda.
Ou seja, os máximos mais próximos do ponto correspondem a diferenças de fase de e .
Interferência destrutiva se dá quando a diferença de fase é um múltiplo fracionário do comprimento de onda. Ou seja, os mínimos mais próximos do ponto correspondem a diferenças de fase de ( ) e ().
Assim, o nosso ponto se encontra entre o 3º mínimo ( ) e o 4º máximo ( ) de interferência (lembre que os primeiros correspondem a ).
Resposta
a)
A diferença de fases corresponde a .
b)
A diferença de fases é igual a .
c)
O ponto se encontra entre o 3º mínimo ( diferença de fase de ) e o 4º máximo (diferença de fase de ) de interferência.
Exercício Resolvido #4
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 104-35.23, modificado.
Duas fendas distantes uma da outra, colocadas a uma distância de de uma tela são iluminadas por uma luz coerente de comprimento de onda igual a .
Qual é a distância sobre a tela entre o centro da franja brilhante central e a primeira franja escura?
Passo 1
O problema nos dá a distância entre as fendas , a distância das fendas para a tela e o comprimento de onda .
Ele nos pede para calcular a distância sobre a tela entre o centro do máximo central e o primeiro mínimo.
Sabemos que os mínimos de interferência são referentes às franjas escuras, onde há interferência destrutiva. Esses pontos são dados por:
Passo 2
Onde:
;
;
;
Como o problema nos pede a posição referente ao primeiro mínimo, isso significa que . Assim:
Logo:
Resposta
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 109-112.
A segunda franja escura em uma figura de interferência de dupla fenda está a do máximo central. A distância entre as fendas é igual a 800 comprimentos de onda da luz monocromática que incide (perpendicularmente) nas fendas.
Qual é a distância entre o plano das fendas e a tela de observação?
Passo 1
Primeiro, vamos lembrar que franjas escuras correspondem a interferência destrutiva.
Sabemos que nesse caso, para pequenos ângulos, vale a seguinte aproximação:
E o enunciado nos algumas informações.
A distância entre as fendas ;
A distância da franja ao máximo central, ;
A franja é a segunda franja escura, (a primeira é ).
Ele nos pede pra calcular . Vamos lá!
Passo 2
Substituindo na fórmula, temos:
Invertendo a fórmula, temos:
Resposta
A distância entre o plano das fendas e a tela de observação é de .
Exercício Resolvido #6
PUC-RIO, Física 4, Prova 1, 2013.2, modificado.
Coloque de falso ou de verdadeiro na afirmação abaixo e justifique a opção.
( ) Se colocarmos o dispositivo de Young (originalmente na água) imerso no ar, as franjas brilhantes se tornarão mais próximas.
Passo 1
A afirmação é FALSA, pois as franjas brilhantes se tornarão mais distantes.
De acordo com o experimento de Young no ar, temos as relações que seguem.
Para franjas claras:
Onde é a distância entre as fendas. Lembre-se que para ângulos pequenos, .
A distância angular entre duas franjas adjacentes é dada por:
Passo 2
Agora, vamos passar esse sistema pra outro meio.
Lembrando que o comprimento de onda depende do meio, pela relação:
Onde é o comprimento da luz no vácuo e é o comprimento de onda da luz em um meio cujo índice de refração é .
Logo, a distância angular em outro meio é dada por:
Como , temos .
Desse modo, temos que as franjas ficarão mais distantes se o experimento for feito no ar!
Resposta
()
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 102-18.
Um sistema de dupla fenda produz franjas de interferência para a luz do sódio () separadas por .
Qual é a separação das franjas quando o sistema é imerso em água ()?
Passo 1
Vimos que quando a luz passa de um meio para outro, sua frequência continua a mesma embora sua velocidade e seu comprimento de onda variem.
Essa variação é dada pelo índice de refração do meio:
Imergir o sistema em água vai alterar o comprimento de onda da luz, alterando a separação das franjas.
Passo 2
As franjas de interferência para duas fendas pontuais são dadas por:
Para duas franjas consecutivas: . No ar, teremos:
Fazendo a aproximação para pequenos ângulos:
E a separação das franjas fica dada por:
Passo 3
Por fim, como vimos antes, a imersão em água afeta o comprimento de onda, e a nova separação vai ser dada por:
Sabemos que a separação angular original é dada por .
Sendo , a nova separação angular vai ser:
Resposta
Exercício Resolvido #8
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 104-35.19.
Em uma figura de interferência com fenda dupla, a intensidade no pico da interferência máxima central é .
- Qual é a intensidade em um ponto da figura de interferência em que a diferença de fase entre as ondas é ?
- Qual a diferença entre os caminhos de uma luz de comprimento de onda igual a proveniente das duas fendas em um ponto em que o ângulo de fase é ?
Passo 1
O problema nos dá a diferença de fase e nos pede para calcular a intensidade no ponto da figura de interferência correspondente.
Sabemos que a relação entre e a intensidade na interferência de duas fontes é dada por
Onde é a diferença de fase. Neste caso, , logo:
Passo 2
A diferença de fase e a diferença de caminho são relacionados por:
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #9
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 104-35.23, modificado
Duas fendas distantes uma da outra, colocadas a uma distância de de uma tela são iluminadas por uma luz coerente de comprimento de onda igual a .
A intensidade no centro do máximo central é igual a .
Qual é a distância sobre a tela entre o centro do máximo central e o ponto no qual a intensidade se reduz a ?
Passo 1
Agora o problema nos pede para encontrar o valor de para o qual .
Sabemos que a intensidade pode ser escrita da seguinte forma:
Isso já nos permite resolver o problema, pois temos os valores de e.
Passo 2
Temos que:
Onde:
;
;
;
Logo:
Resposta
Exercício Resolvido #10
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 104-35.11.
Uma luz coerente proveniente de uma lâmpada de vapor de sódio passa através de um filtro que bloqueia tudo e deixa passar um único comprimento de onda.
A seguir ela incide sobre duas fendas separadas por uma distância de .
Na figura de interferência formada sobre uma tela situada a uma distância de , a distância entre duas franjas brilhantes adjacentes é igual a .
Qual é o comprimento de onda?
Passo 1
O problema nos dá o valor da distância entre as fendas , a distância entre as fendas e o anteparo e nos diz a distância entre duas franjas brilhantes adjacentes.
Vale lembrar que as franjas brilhantes referem-se a pontos de interferência construtiva.
Podemos relacionar todas as grandezas dadas pelo problema com o comprimento de onda através da equação de para interferência construtiva, dada por:
Passo 2
O problema nos diz que a distância entre duas franjas brilhantes adjacentes vale .
A distância entre as franjas é dada por:
Portanto:
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 107-93.
Duas fendas paralelas são iluminadas com uma luz monocromática cujo comprimento de onda é 500nm. Uma figura de interferência aparece em uma tela situada a uma certa distância das fendas, e a quarta franja escura está a da franja clara central.
- Qual é a diferença de percurso correspondente à quarta franja escura?
- Qual é a distância na tela entre a franja clara central e a primeira franja clara de cada lado da franja central?
(Sugestão: Os ângulos da quarta franja escura e da primeira franja clara são tão pequenos que )
Passo 1
a)
Primeiramente, ele nos pede a diferença de percurso correspondente à quarta franja escura.
Como a franja é escura, ela corresponde a um mínimo de interferência. Como vimos antes, a diferença de percurso para franjas escuras é da por:
Para a 4ª franja escura, temos (a primeira corresponde a ).
Além disso, temos o comprimento de onda .
Substituindo esses valores na nossa expressão, obtemos que a diferença de percurso é:
Passo 2
b)
Temos pelo menos 2 formas de pensar a solução da letra b. A primeira e mais direta é substituir a distância da quarta franja clara na fórmula de distância (para ângulos pequenos), e seguir daí.
Aí reconhecemos que a distância dos primeiros máximos laterais é (substituímos ).
A segunda forma é matematicamente igual, mas vamos discorrer um pouco mais sobre o significado das fórmulas.
Passo 3
Primeiro, precisamos lembrar que a distância entre duas franjas clara consecutivas, para pequenos ângulos, é constante e dada por:
Assim, a distância do máximo central até a quarta franja clara é igual a sua distância até a primeira franja clara, e depois dessa até a quarta franja clara.
Mas como a distância entre franjas clara consecutivas é constante, a distância da primeira franja clara até a quarta franja clara é dada por (da 1ª pra 2ª, da 2ª pra 3ª e da 3ª pra 4ª são 3 vezes ).
Já a distância da primeira franja clara até a franja brilhante central é:
Logo, a distância do máximo central até a quarta franja clara é:
Substituindo a distância de , temos:
Passo 4
Por fim, note que os primeiros máximos centrais laterais ( ) são os próximos depois do central. O central e eles são consecutivos.
Como a distância entre duas franjas brilhantes é igual a distância entre duas franjas claras
Mas por que perder tempo pensando a questão dessa forma, se a outra era tão direta?
O interessante de pensar a questão dessa segunda forma é que ela nos lembra de dois pontos importantes (que valem quando os ângulos são pequenos):
- A distância entre duas franjas (brilhantes ou claras) consecutivas é constante;
- A distância entre duas franjas brilhantes consecutivas é igual a distância entre duas franjas claras consecutivas.
Resposta
a)
A diferença de percurso referente à quarta franja escura é .
b)
A distância na tela entre a franja clara central e as primeiras franjas claras laterais é .
Exercício Resolvido #12
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 104-35.15.
Uma luz coerente com um comprimento de onda de passa por duas fendas muito estreitas e a figura de interferência é vista em um anteparo a das fendas.
A primeira franja brilhante está a do centro da franja brilhante central.
Em que comprimento de onda da luz a primeira franja escura será vista no mesmo ponto do anteparo?
Passo 1
O problema nos dá o comprimento de onda , a distância entre as fendas e o anteparo , e a posição da primeira franja brilhante .
O problema nos pede para calcular um comprimento de onda que faça com que a primeira franja escura seja vista no mesmo ponto .
Os pontos onde encontramos as franjas escuras (mínimos de interferência) sobre o anteparo são dados por:
Entretanto, na equação acima nos faltam 2 dados: o comprimento de onda (que é o que queremos descobrir) e a distância entre as fendas .
Para descobrir o valor de , podemos usar as informações dadas pelo problema, aplicando à equação para franjas brilhantes (máximos de interferência):
Passo 2
Encontrando o valor de .
Conforme falamos antes, a equação que vai nos ajudar é esta:
Onde:
;
;
;
;
Logo:
Observação: corresponde ao comprimento de onda usado para a situação em que estávamos trabalhando com a franja brilhante.
Passo 3
Onde:
;
;
;
;
Observação: corresponde ao comprimento de onda usado para a situação em que estávamos trabalhando com a franja escura.
Resposta
Exercício Resolvido #13
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 103-34
No experimento de dupla fenda da Fig.35-10, a tela de observação está a uma distância, o ponto está a uma distância do centro da figura de interferência, a distância entre as fendas é e o comprimento de onda é .
- Determine a posição do ponto na figura de interferência, indicando o máximo ou mínimo em que se encontra ou o máximo e o mínimo entre os quais se encontra.
- Calcule a razão entre a intensidade no ponto e a intensidade no centro da figura de interferência.
Passo 1
a)
Nesta questão, vamos considerar que os ângulos são suficientemente pequenos. Para ver como isso é válido, note que o ângulo correspondente ao ponto é dado por
O ângulo vai ser:
Que é bem pequenininho.
Passo 2
Usando a aproximação de pequenos ângulos, sabemos que a diferença de fase no ponto , em múltiplos do comprimento de onda, é de:
Sendo que o problema nos dá:
A distância entre as fendas é ;
A distância do ponto ao centro da figura é ;
A distância da tela de observação é ;
O comprimento de onda é .
Assim:
Que está entre (o máximo central) e (o primeiro mínimo).
De fato, notemos que a posição do primeiro mínimo é
Que está logo depois da posição do ponto .
Passo 3
b)
A intensidade em um ponto P qualquer é dada por
Ou seja, a razão é dada por , onde é a diferença de fase em radianos:
Substituindo, temos:
Resposta
a)
O ponto se encontra entre o máximo central e o primeiro mínimo ( para ambos).
b)
A razão entre a intensidade no ponto e a intensidade no centro da figura é 0,10 (ou seja, corresponde a de ).