Efeito Fotoelétrico
Produzido por Bruno SoaresTeoria
O efeito fotoelétrico é um fenômeno quântico que consiste na emissão de elétrons por um material exposto a uma radiação eletromagnética, como a luz, em uma frequência suficientemente alta.
Como Funciona o Efeito Fotoelétrico?
Antes de qualquer coisa, pra ficar mais claro o que é o efeito fotoelétrico, se liga na imagem abaixo:
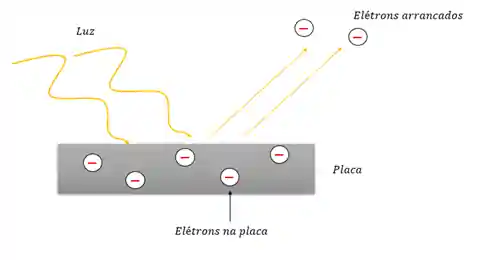
O efeito fotoelétrico geralmente acontece em materiais metálicos. Quando a luz incide na superfície do material, ela arranca elétrons da placa. Ou seja as ondas eletromagnéticas envolvidas nesse fenômeno transferem energia aos elétrons, é por isso que os elétrons são ejetados!
Ahh, eles elétrons que são “arrancados” do metal são chamados de fotoelétrons!
Para o efeito fotoelétrico acontecer a radiação incidida na superfície do material deve ceder energia suficiente pra ejetar os elétrons. Mas não se engane, isso não depende da intensidade da luz e sim da sua frequência!
-Mas por que isso acontece?!
Excelente pergunta! Quando a luz incide sobre a superfície metálica os fótons da luz colidem com os elétrons e são absorvidos, provocando a emissão dos elétrons pela superfície.
Função Trabalho
Sabemos que para que o efeito fotoelétrico aconteça, precisamos ceder uma energia mínima para os elétrons do metal.
-Mas como calcular essa energia?!
É o que vamos aprender aqui, mas vamos por partes!
A energia cedida pelo fóton precisa ser maior que a energia de ligação dos elétrons para conseguir ejetá-los. Então o primeiro passo é saber qual é a energia do fóton:
Onde,
Agora, a energia de ligação dos elétrons a superfície é chamada Função Trabalho do Material e cada material possui uma função trabalho definida, e nas continhas vai aparecer como
Independente da intensidade da luz, um elétron ejetado absorve a energia de apenas um fóton! Podemos então, igualar a energia do fóton com a função trabalho, para ver qual frequência ou comprimento de onda seriam necessários para remover o elétron:
A gente pode dizer então que a função trabalho é a energia mínima que o fóton precisa ter pra fazer com que aconteça o efeito fotoelétrico.
Para essa energia mínima a gente vai ter uma frequência relacionada, chamada frequência de corte
Além da frequência um outro limite é o comprimento de onda, também teremos um comprimento de onda de corte
Vamos reescrever então a equação de cima em função desses limites:
Exemplo: Como Calcular a Frequência de Corte
Vamos colocar isso em prática! Qual seria a frequência de corte e o comprimento de onda de corte necessários pro fóton ser capaz de arrancar elétrons de uma placa de alumínio?
Dados:
Bora lá, primeiro é bom lembrar que a função trabalho é a energia mínima pro efeito fotoelétrico acontecer:
Então a energia mínima do fóton depende da frequência de corte:
Substituindo temos:
E agora o cálculo do
Então o efeito fotoelétrico vai acontecer para:
Sacou?!
Aplicação do Efeito Fotoelétrico
No dia a dia a gente pode observar uma aplicação pratica do efeito fotoelétrico! Já reparou naqueles painéis solares capazes de transformar a energia luminosa do sol em eletricidade?!
Então, é o efeito fotoelétrico todinho na prática!!

Maneiro, não é?! 🤩🤩🤩
Vídeo Aula
Ficou alguma dúvida?!
Confere então esse vídeo supercompleto sobre efeito fotoelétrico! 👇
Bora praticar com exercícios?!