Condução de Calor
Teoria
Fala aí! Seja muito bem vindo ao RespondeAí! Bora aprender TUDO sobre condução de calor?!
A condução térmica é um processo de transferência de calor de um corpo com maior temperatura para um de menor temperatura até que se atinja o equilíbrio térmico.
Mas atenção! Pra que a condução ocorra, os corpos de diferentes temperaturas precisam estar em contato!
Vamos imaginar a seguinte situação, você segura uma colher e coloca no fogo e continua segurando a colher (por favor não faça isso 🤣🤣🤣), você vai sentir a colher esquentando e se você continuar ali sua mão vai queimar, certo?!
Na condução o calor é transferido pela vibração das moléculas, de molécula em molécula!
Agora vamos entender como calculamos isso!
Taxa de Condução de Calor
A taxa de condução de calor é o quanto calor que passa por um material por unidade de tempo,
Imagine que temos duas fontes de calor onde
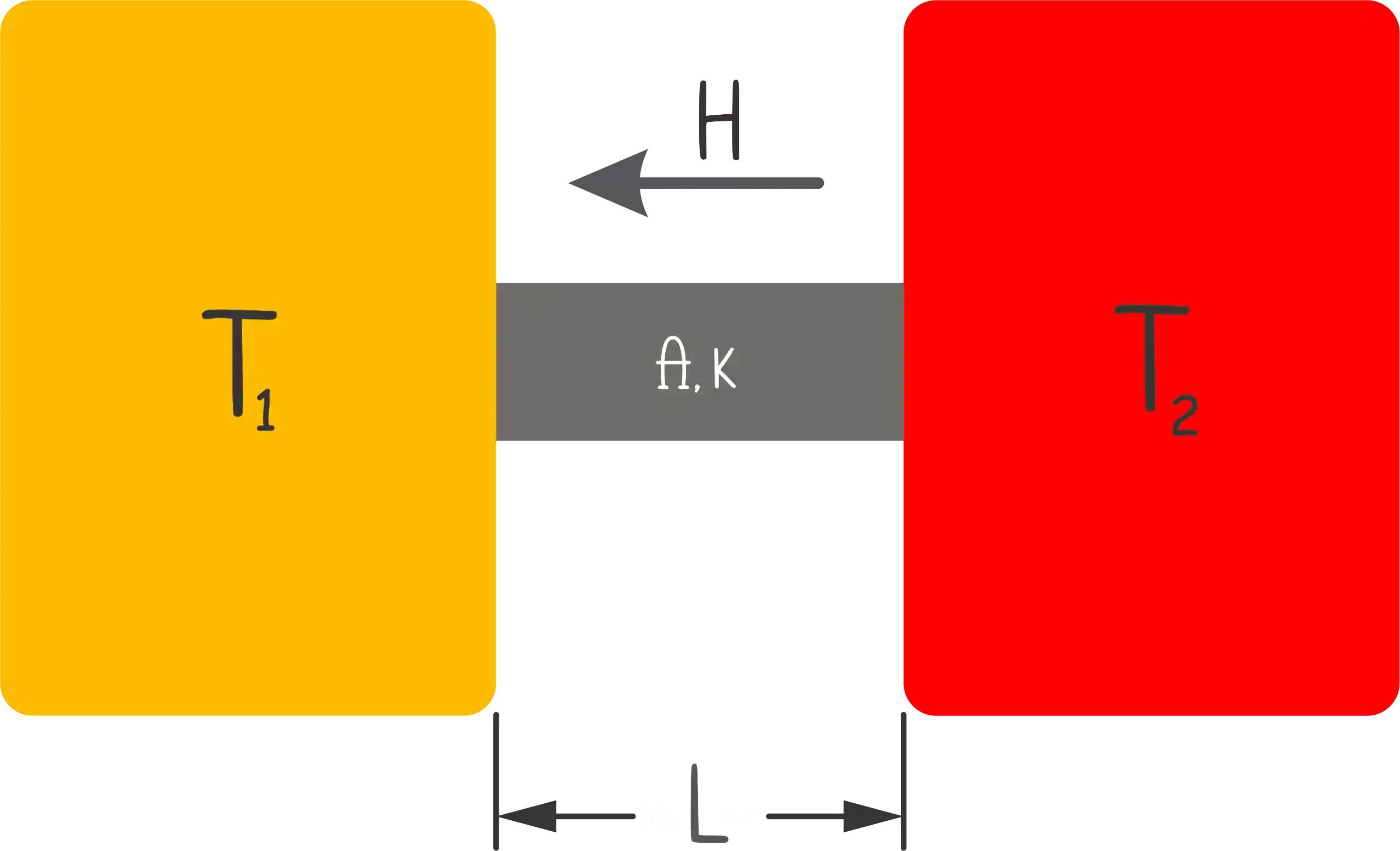
A taxa de condução de calor pode ser dada pela seguinte fórmula:
Lei de Fourier
Podemos calcular a taxa de condução térmica, também, através da seguinte fórmula:
onde:
é a condutividade térmica (propriedade do material) e a sua unidade no SI é é a área por onde o calor está sendo propagado; é a espessura na direção do fluxo de calor; é a diferença de temperatura entre as duas fontes;
Resistência Térmica
Todo material apresenta uma certa resistência à transferência de calor, dificultando-a. Medimos essa resistência pela seguinte fórmula:
A unidade no SI da resistência térmica é
A fórmula da condução de calor pode ser reescrita como:
Beleza! Tudo muito bom, tudo muito bem.
Mas e se juntarmos os materiais? Como seria uma associação em série ou em paralelo de condutores térmicos?
Associação em Série
Esse é o caso em que colocamos um material após o outro, assim:
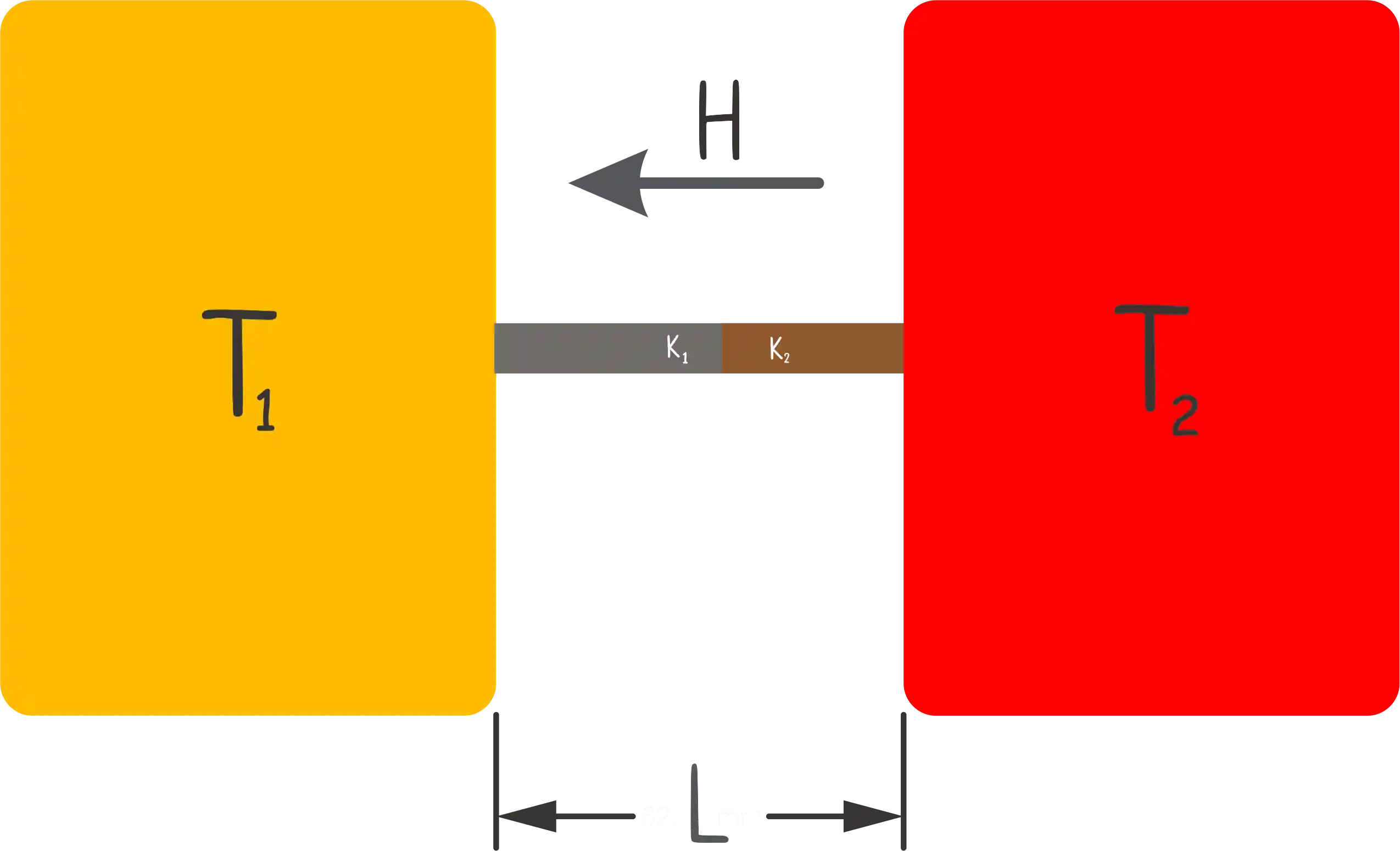
Para condutores em série, temos que usar a conservação de energia. Todo calor que passa por um dos materiais tem que passar pelo outro também.
Repare que no ponto de contato dos dois, temos uma temperatura intermediária
Podemos cortar a área:
E escrever em função das resistências térmicas
Substituindo isso na equação para
Se os condutores forem de mesmo material:
Nesse caso, basta substituir o comprimento pela soma dos comprimentos:
É como se substituíssemos por um único condutor de mesma área e cujo comprimento é a soma dos comprimentos dos condutores.
Associação em Paralelo
Associar em paralelo é colocar um material do lado do outro, assim:
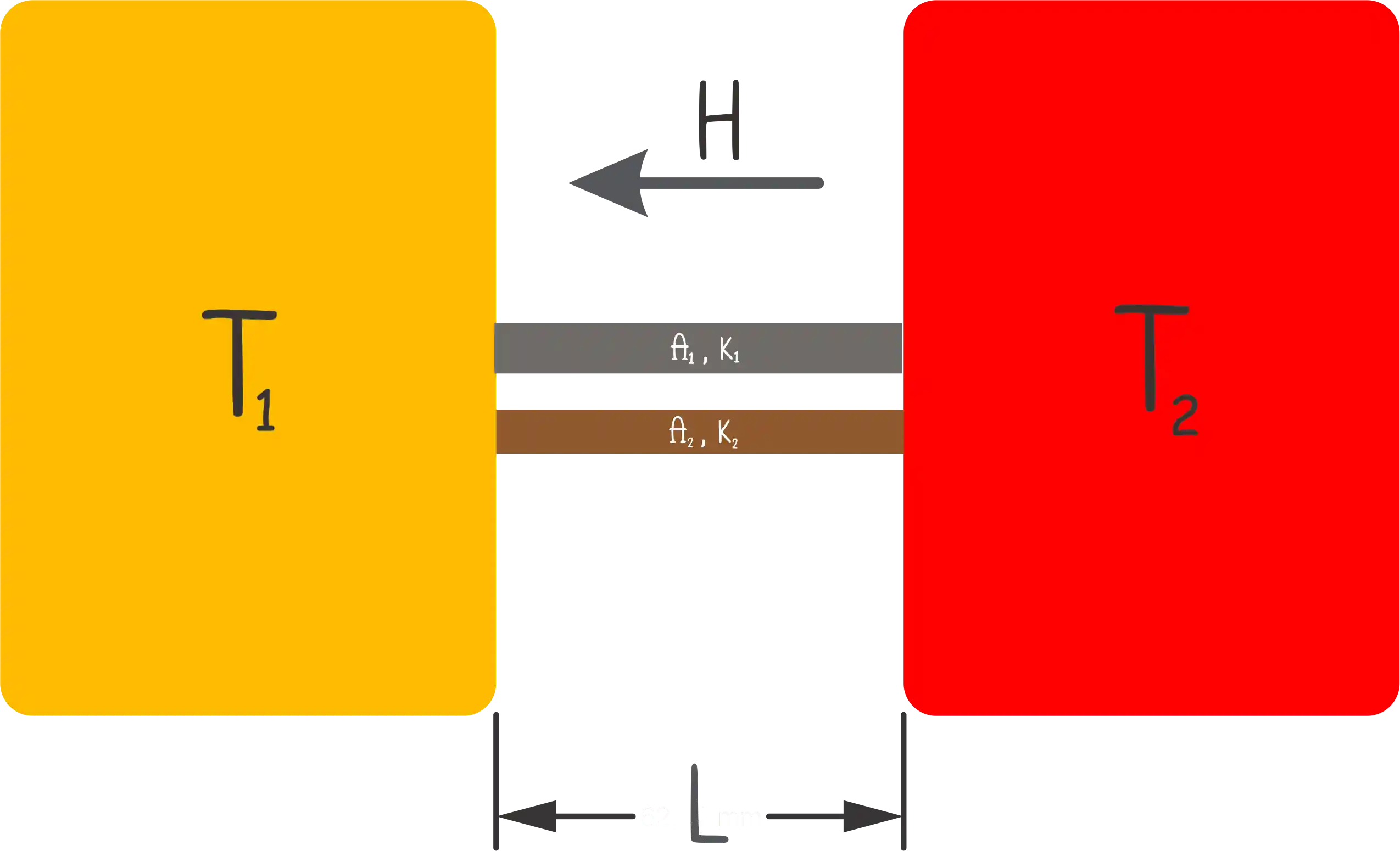
Para condutores em paralelo, o calor pode fluir tanto pelo material de cima quanto pelo debaixo, então a taxa total vai ser:
Ou escrevendo em função das resistências térmicas:
Se os condutores forem de mesmo material, então as constantes
Então temos que todas as resistências são iguais:
Nesse caso, basta substituir a área pela soma das áreas:
Condução, Convecção e Radiação: Diferenças
- Condução
É quando o calor atravessa um material, átomo a átomo, do corpo mais quente até o mais frio.
Os materiais que fazem isso de forma rápida são chamados condutores térmicos, por exemplo os metais. Os que fazem isso de forma bem lenta são os isolantes térmicos, tipo a madeira.
- Convecção
É o transporte através do movimento de um fluido causado pela diferença de densidade que ocorre pela variação de temperatura. Pera aí, o que?
Você já percebeu que o freezer é sempre na parte superior das geladeiras? Por quê? Para que ocorra a convecção!
O freezer vai esfriar o ar que está lá em cima, o ar frio por ser mais denso que o ar quente vai então descer deslocando o ar quente para cima. Esse novo ar quente vai ser resfriado pelo freezer e assim sucessivamente, gerando correntes de convecção, que esfriam toda a geladeira.
- Radiação
É a transmissão de calor por ondas eletromagnéticas. Assim, o calor não precisa de nenhum meio para se propagar. Por exemplo o calor do Sol, que chega até a Terra atravessando o vácuo espacial.
Mas essas duas últimas são pouco estudadas.
Exercício
O teto de uma casa em uma cidade de clima frio deve ter uma resistência térmica
Confira a resposta no vídeo abaixo:
Vamos praticar com mais exercícios?!
Resistência Térmica
Condução, Convecção e Radiação: Diferenças
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 210. x-y 54
O teto de uma casa em uma cidade de clima frio deve ter uma resistência térmica de . Para isso, qual deve ser a espessura de um revestimento de espuma de poliuretano e de prata?
Dados:
Passo 1
O problema quer saber a espessura do material para que a resistência térmica seja de , para isso vamos usar a fórmula de resistência
Passo 2
O enunciado nos deu o do poliuretano então basta substituir na fórmula
Passo 3
Fazemos o mesmo para a prata agora
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 210. x-y 51
Considere a placa da figura abaixo. Suponha que , e que o material é cobre. Se , e um regime estacionário é atingido, determine a taxa de condução de calor através da placa. Dados:
Passo 1
O problema quer que determinemos a taxa de condução de calor da placa de cobre. Para isso vamos usar a fórmula de taxa de condução de calor que acabamos de aprender na teoria
Repare que como estamos tratando de uma VARIAÇÃO DE TEMPERATURA não precisamos converter pra Kelvin, porque a variação na escala Celsius é a mesma na escala Kelvin.
Passo 2
O enunciado nos forneceu tudo que precisamos, então basta substituir na fórmula
Repare que como a variação da temperatura é igual em Celsius e Kelvin, não precisamos transformar.
Lembre-se apenas de usar as unidades do SI, por isso transformamos tudo que ele deu em para .
Assim
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 210. x-y 53
Uma barra cilíndrica de cobre de de comprimento e de seção reta é bem isolada e não perde energia através da superfície. A diferença de temperatura entre as extremidades é , já que uma está imersa em uma mistura de água e gelo e a outra em uma mistura de água e vapor. Com que taxa a energia é conduzida pela barra? Com que taxa o gelo derrete na extremidade fria? Dados e
Passo 1
Esse item consiste em uma questão de condução de calor e por isso vamos usar a fórmula que acabamos de aprender
Como o enunciado nos forneceu tudo para calcularmos , basta substituirmos na fórmula
Obs.: Na diferença de temperatura para colocar em Kelvin, não foi preciso fazer nenhuma conversão!
Porque, como a diferença entre temperaturas é de 100°C, se colocarmos por exemplo a temperatura inicial igual a 0°C e a final igual a 100°C, teremos a simplificação:
Isso é, se tratando de diferenças de temperatura, não importa se é Celsius ou se é Kelvin, vai dar no mesmo ;)
Passo 2
Já esse item é um problema onde o gelo está se transformando em água, quando transferimos calor a uma substância e ela muda de estado e por isso a temperatura se mantém a mesma te lembra de algo? Isso, calor latente.
Se lembrarmos que a forma que usamos em casos como esse é
Você vai perceber que temos um grande problema pois não temos nem a massa de gelo nem a quantidade de calor transferida ao gelo.
A sacada desse item é que ele pede a taxa de gelo que está se transformando em água, ou seja, quanto de gelo em está virando água, assim podemos dividir os dois lados da equação acima pelo tempo e ficamos com
Agora sim, pois
E é o que queremos, agora podemos substituir os valores que temos para achar a taxa de gelo transformada em água
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 212-74
A taxa média com a qual a energia chega à superfície do solo na América do Norte é , e a condutividade térmica média das rochas próximas da superfície é . Supondo que a temperatura da superfície é de , determine a temperatura a uma profundidade de (perto da base da crosta). Ignore o calor gerado pela presença de elementos radioativos.
Passo 1
O problema nos pede a temperatura de um lado da crosta terrestre. Nos fornecendo a condutividade térmica das rochas que formam a crosta terreste, a comprimento e ainda nos dá a taxa de calor que é conduzida.
Então temos tudo que caracteriza uma questão de condução de calor e por isso iremos usar a fórmula
Passo 2
Vamos achar qual foi a variação de temperatura, já que ela será igual tanto em graus Celsius quanto para Kelvin. Assim
Bom, agora basta substituir os valores que temos
Ué, mas não está faltando a área ? Não, porque o problema nos forneceu a taxa média de , que é , pode confirmar isso pela unidade.
Então,
Como já foi dito no início desse passo, a variação de temperatura em Kelvin é igual para graus Celsius, logo
E como a variação da temperatura é a temperatura final menos a inicial
Substituindo
Resposta
Exercício Resolvido #5
CEFET – Prova Final - Vance
A parede externa de uma casa tem uma camada de de madeira por fora e uma camada isolante de isopor também de de espessura por dentro. Se a madeira possui coeficiente de condutibilidade térmica ,a condutividade térmica do isopor , a temperatura externa for de e a temperatura no interior de , calcule:
A temperatura no ponto em que a madeira encontra o isopor.
Qual a taxa de fluxo de calor, em , através da parede?
Figura auxiliar:
Passo 1
Bom galera, a ideia central dessa questão é simples: A energia se conserva. Isso quer dizer que toda a energia que passar por uma das placas deve passar pela outra, certo?
E qual será o pulo do gato? Vamos igualar as taxas de transferência de calor das duas placas:
Passo 2
Vamos escrever agora as expressões para as duas taxas de transferência:
-Isopor:
Usando os dados do enunciado:
Sendo a temperatura da interseção. (O que queremos achar).
-Madeira:
Fazendo:
Passo 3
Agora queremos calcular a taxa de energia através da parede. Fácil! Basta a gente calcular a taxa através da madeira ou através do isopor. Vamos lá:
Resposta
Exercício Resolvido #6
CEFET – Prof. Carolina
Temos uma barra de alumínio de comprimento e área transversal de isolada com cortiça; um termômetro fixo na barra calibrado em Farhenheit, e dois dispositivos, e que proporcionam nas extremidades da barra, as temperaturas e , respectivamente. Considerando a intensidade da corrente térmica constante ao longo da barra, determina a temperatura registrada no termômetro, sabendo que ele se encontra a do dispositivo
Dado:
Passo 1
Bom galera, nessa questão usaremos o conceito de condução de calor. O pulo do gato dessa questão será considerar o princípio da conservação da energia.
Se a energia não se perde, a taxa de condução deve ser a mesma ao longo de toda a barra, certo?
E esse é o pulo do gato. Vamos igualar as taxas de condução de calor para descobrir a temperatura do termômetro.
Mas antes, vamos converter os valores das extremidades para Kelvin:
Para agora
Passo 2
A gente quer achar a temperatura do ponto onde está o termômetro. Vamos chama-la de .
Vamos escrever a primeira taxa, a referente ao comprimento de :
Vamos deixar assim por enquanto.
E a taxa da segunda parte será:
Passo 3
Igualando as duas taxas:
Resposta
Exercício Resolvido #7
UFRJ – 1ª Prova – 2012.2
Dois cilindros longos, finos, sólidos e idênticos são utilizados para conduzir calor de um reservatório quente para outro frio. Sabendo que na configuração à esquerda (na figura abaixo) a taxa de transferência de calor é , qual o valor da taxa de transferência de calor para a configuração da direita?
Passo 1
Bom, a taxa de transferência de calo de um condutor é dada por:
Então vamos considerar que vale:
Onde é a soma do comprimento das duas barras
Passo 2
Bom, como o enunciado disse que as barras são idênticas, então:
Onde representa o comprimento do condutor na figura da direita.
Além de termos diminuído o comprimento pela metade, ainda dobramos a área, certo(podemos notar isso de acordo com a figura do enunciado)?
Assim, substituindo na fórmula de condução:
Resposta
Alternativa
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 210. x-y 57
Na figura abaixo, as duas barras retangulares iguais de metal são soldadas nas extremidades e mantidas a uma temperatura de do lado esquerdo e uma temperatura de do lado direito. Em , são conduzidos a uma taxa constante do lado direito para o lado esquerdo. Que tempo seria necessário para conduzir se as placasa fossem soldadas lado a lado como na Figura abaixo?
Passo 1
Essa questão pede para que comparemos a condução em uma associação em serie de condutores com uma associação em paralelo . Para isso vamos analisar cada caso separado e depois compará-los.
No caso onde a associação é em serie temos:
Lembrando que
Temos
Substituindo os valores que temos
Podemos isolar as letras, isso vai facilitar na hora de comparar as associações
Passo 2
Agora vamos analisar a associação em paralelo
Com os dados que temos podemos substituir na fórmula de condução de calor
A última coisa que calculamos no “passo 1” foi
Podemos substituir isso na equação de condução em paralelo
Assim chegamos que o tempo necessário seria de
Resposta
Exercício Resolvido #9
UERJ – Lista da 2ª Prova
A figura mostra (em seção transversal), uma parede composta de quatro camadas, com condutividade térmica , e (não é conhecida). As espessuras das camadas são , e não é conhecida). A transferência de energia através da parede é estacionária. Qual a temperatura na interface entre as camadas 3 e 4?
Passo 1
Bom, galera, primeiramente, o que significa dizer que há uma transferência de energia estacionária?
A ideia de um sistema estacionário é que não varia com o tempo e isso geralmente está ligada ao conceito de conservação!
Logo, isso quer dizer que todo o calor que entra também sai! Nesse problema, isso quer dizer que as taxas de transferência de calor das camadas são iguais! Então, sendo a taxa de transferência de calor que é dada por:
Onde:
: Condutividade térmica.
: Área da transferência de calor.
: Comprimento do condutor
: Diferença de temperatura, tal que ;
Teremos:
Passo 2
Mas saber que as taxas são iguais nos ajuda em quê? Bom, o problema nos diz que o sistema tem várias coisas desconhecidas (. Só que a gente só quer descobrir o !
Repare que o a temperatura é a temperatura da extremidade esquerda da camada 4. Se a gente soubesse essa temperatura, daria pra calcular a taxa de transferência dessa camada, certo?
Ela ficaria assim:
Por que calculamos a diferença de temperatura assim? Bom, como o calor flui da maior temperatura para a menor, ao menos de forma natural, a gente espera que seja maior que . (Lembra que na fórmula é maior que ?).
Aí vem o pulo do gato: Como as taxas de calor são iguais, vamos comparar essa taxa com a incógnita a uma taxa conhecida. A taxa que podemos calcular facilmente é a da camada 1. Então:
Pronto! Agora vamos resolver essa equação para achar ! (:
Passo 3
Vamos resolver a equação agora. Os dados que temos são:
Na equação ficará:
Cortando o e fazendo simplificações:
Perceba que . O que era o esperado (: