P1 de Física 2- FIS1041 da PUCRIO - 2011.2

Dentro de uma garrafa aberta para a atmosfera, contendo água (), flutua parcialmente submerso um tubo invertido, com o lado aberto para baixo. O interior do tudo é parcialmente ocupado por água, como mostrado na figura ao lado. O espaço restante () é ocupado por ar.

O tubo tem paredes rígidas muito finas (volume das paredes desprezível). O seu comprimento é e a sua seção transversal é quadrada de lado .

Observa-se que e .

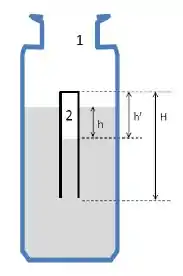
1. Calcule a pressão manométrica na interface água-ar dentro do tubo. Qual a pressão manométrica do ar preso no tubo?
2. Considere o conjunto (paredes do tubo + ar preso). Usando o princípio de Arquimedes determine a força de empuxo sobre esse conjunto. Indique sua direção e sentido.
3. Calcule a força que o ar exerce sobre a superfície superior do tubo (considere tanto a sua face interna quanto externa). Indique claramente a direção e sentido da força resultante. Compare o resultado com o achado no item B.
4. Ache a massa do tubo.
5. Se a pressão externa (em ) é aumentada, depois de um tempo uma nova situação de equilíbrio é alcançada, em que o tubo passa a flutuar completamente imerso. Nessa situação, determine o volume ocupado pelo ar preso.

Um riacho de efluentes industriais líquidos () de largura e profundidade corre a céu aberto.

O riacho passa depois a ser canalizado em uma tubulação com seção reta circular de diâmetro , que correão longo da horizontal de modo que o seu eixo central está a abaixo do nível médio do rio.

Finalmente, o líquido é lançado num jato horizontal para a atmosfera.

Observa-se que a velocidade do riacho, , é aproximadamente horizontal e uniforme ao longo de toda seção reta. Considere os fluxos sempre laminares e uniformes. Considere e .

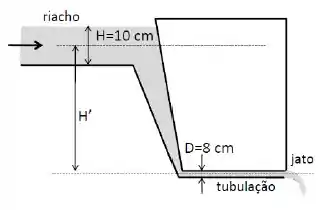
1. Calcule a vazão do riacho.
2. Calcule a velocidade do líquido dentro da tubulação horizontal.
3. Calcule a pressão num ponto qualquer dentro da tubulação.
4. Calcule a profundidade da tubulação.

Um pêndulo simples formado por uma esfera de massa suspensa por um fio vertical encontra-se em repouso. Uma bala de espingarda de chumbinho, de massa , atinge a esfera horizontalmente e fica alojada nela.

O gráfico abaixo representa a posição angular do conjunto pêndulo-bala em função do tempo.

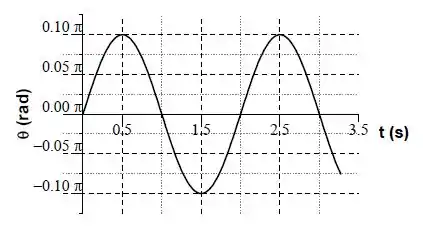
1. Encontre o ângulo máximo () e a frequência angular () desse movimento.
2. Escreva uma expressão literal para a função . Encontre a constante de fase e escreva os valores numéricos de todos os parâmetros dessa expressão (com unidades).
3. Determine o comprimento do pêndulo e a velocidade máxima que ele atinge.
4. Calcule a velocidade da bala imediatamente antes de atingir o pêndulo.