Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pêndulos Simples

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738

Enunciado

MHS

Um pêndulo simples formado por uma esfera de massa M = 0,198   k g suspensa por um fio vertical encontra-se em repouso. Uma bala de espingarda de chumbinho, de massa m = 2,0   g , atinge a esfera horizontalmente e fica alojada nela.

O gráfico abaixo representa a posição angular do conjunto pêndulo-bala em função do tempo.

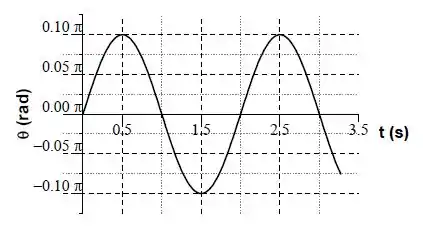
  1. Encontre o ângulo máximo ( θ m ) e a frequência angular ( ω ) desse movimento.
  2. Escreva uma expressão literal para a função θ ( t ) . Encontre a constante de fase e escreva os valores numéricos de todos os parâmetros dessa expressão (com unidades).
  3. Determine o comprimento do pêndulo e a velocidade máxima que ele atinge.
  4. Calcule a velocidade da bala imediatamente antes de atingir o pêndulo.

Passo 1

a): O ângulo máximo pode ser encontrado por uma simples inspeção no gráfico nos seus valores pico. Esse valor é θ M = 0,10 π .

A gente pode calcular a frequência angular usando o valor do período do movimento. Pra achar o período, vamos pegar os valores de tempo de dois picos consecutivos. Por exemplo, o primeiro pico acontece em t = 0,5 s e o segundo em t = 2,5 s .

O ∆ t = 2,0 s e esse é o valor do período. Então, usando a fórmula da frequência angular:

ω = 2 π T = 2 π 2 = π = 3,14 r a d / s

Passo 2

b):

A função angular de t vai ser da forma:

θ t = θ M s e n ( ω t + φ )

Para t = 0 , temos θ = 0 , logo:

0 = θ M s e n φ → φ = k π

Ou seja, a fase é um múltiplo de π . Agora, como, pelo gráfico, o valor da derivada em zero é positivo(veja a inclinação do gráfico no ponto ( 0,0 ) ) , temos que:

d θ t d t > 0 → ω θ M cos ⁡ φ > 0 → φ = 0

Por que para que seja positivo, teremos que ter o cosseno positivo, e isso acontece quando φ = 0 .

Logo:

θ t = θ M s e n ω t + φ = π s e n π t = 0,3 14 s e n ( 3,14 t )

Os valores numéricos e as unidades são:

θ M = 0,3 14 r a d

ω = 3,14 r a d / s

t = s

E o tempo é dado em segundos.

Passo 3

c):

Usando a expressão do período:

T = 2 π l g   → T 2 4 π 2 = l g ↔ ω 2 = g l   ↔ l = g ω 2

Usando os valores que encontramos:

l = g ω 2 = 10 π 2 ≅ 1,01 m

Bom, a velocidade máxima acontece para o valor máximo da derivada temporal da expressão θ t :

θ t = 0,1 π s e n π t → d θ t d t = 0,1 π 2 c o s ⁡ ( π t )

Isso acontece para cos ⁡ π t = 1

Logo,a derivada máxima é:

d θ t m á x d t = 0,1 π 2

No entanto, esse é o valor pra velocidade angular máxima. Queremos a linear. Basta multiplicarmos o valor acima por l :

v m á x = π 2 l = 0,1 π 2 . 1,01 ≅ 1 m / s

Passo 4

d):

Vamos usar a conservação do momento linear aqui. O momento inicial, devido à bala. É dado por:

Q i = m b a l a . v b a l a

O momento final é dado por:

Q f = m b a l a + M p e n d u l o v m á x

Logo, usando os valores que calculamos e os valores do enunciado:

Q i = Q f

∴

m b a l a . v b a l a = m b a l a + M p e n d u l o v m á x

∴

v b a l a = m b a l a + M p e n d u l o v m á x m b a l a = 0,198 + 0,002 x 1 0,002 ≅ 100 m / s

Resposta

a):

3,14 r a d / s  

b):

θ t = 0,314 s e n ( 3,14 t )

c):

v m á x ≅ 1 m / s

d):

v b a l a = 100 m / s

Exercícios de Livros Relacionados

Suponha que um pêndulo simples é formado por um pequeno peso de 60,0 g pendurado na extremidade de uma corda de massa desprezível. Se o ângulo θ entre a corda e a vertical é dado por θ = 0,0800rad cos
Uma artista de circo, sentada em um trapézio, está balançando com um período de 8,85 s . Quando fica de pé, elevando assim de 35,0 c m o centro de massa do sistema t r a p é z i o + t r a p e z i s t
Mostre que a energia total de um pêndulo simples sob oscilações de pequena amplitude ϕ 0 (em radianos) é E ≈ 1 2 m g L ϕ 0 2 . Dica: Use a aproximação c o s ϕ ≈ 1 - 1 2 ϕ 2 para pequenosϕ .
No Planeta X , onde o valor de g é desconhecido, um pêndulo oscila com período T = 2s . Qual será o período deste pêndulo se: a. Sua massa for duplicada? Explique. Note que você não sabe quais são os
Na figura, uma mola de demolição de 2500k g balança na ponta de um guindaste. O comprimento do segmento de cabo que se move com a bola é 17m . (a) Determine o período do balanço, supondo que o sistema