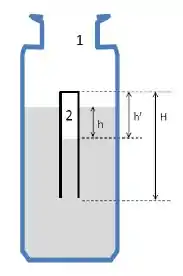
Dentro de uma garrafa aberta para a atmosfera, contendo água (), flutua parcialmente submerso um tubo invertido, com o lado aberto para baixo. O interior do tudo é parcialmente ocupado por água, como mostrado na figura ao lado. O espaço restante () é ocupado por ar.
O tubo tem paredes rígidas muito finas (volume das paredes desprezível). O seu comprimento é e a sua seção transversal é quadrada de lado .
Observa-se que e .
- Calcule a pressão manométrica na interface água-ar dentro do tubo. Qual a pressão manométrica do ar preso no tubo?
- Considere o conjunto (paredes do tubo + ar preso). Usando o princípio de Arquimedes determine a força de empuxo sobre esse conjunto. Indique sua direção e sentido.
- Calcule a força que o ar exerce sobre a superfície superior do tubo (considere tanto a sua face interna quanto externa). Indique claramente a direção e sentido da força resultante. Compare o resultado com o achado no item B.
- Ache a massa do tubo.
- Se a pressão externa (em ) é aumentada, depois de um tempo uma nova situação de equilíbrio é alcançada, em que o tubo passa a flutuar completamente imerso. Nessa situação, determine o volume ocupado pelo ar preso.
Passo 1
a):
A pressão manométrica é definida como a pressão absoluta que você vai calcular menos a pressão atmosférica:
Bom, mas pra calcular a pressão na interface interna do tubo a gente precisa usar o teorema de Steven: Esse teorema nos diz que a pressão da água interna ao tubo é a mesma que a pressão da água no lado de fora do tubo, já que estão à mesma altura.
A pressão no lado de fora é:
Logo, a pressão manométrica da interface é:
Agora, qual a pressão manométrica do ar? Bem, como o ar exerce pressão na água através da interface, a pressão do ar será exatamente igual à pressão da interface.:
Passo 2
b):
O empuxo é dado por:
Sendo o volume submerso. Vamos então calcular o volume submerso e a partir dai o empuxo.
Desconsiderando o volume das paredes, o volume submerso é dado por:
Onde é a área da seção transversal do tubo. Usando os dados do problema:
Logo o empuxo será:
E qual a direção do empuxo? Bem, ela será na direção contrária ao peso:
Já que o peso é na direção
Passo 3
c):
A força pode ser calculada usando-se a pressão pela relação:
Onde é a área. A força externa será dada então por:
E a força interna será:
A resultante será dada por:
Lembrando que ali é a pressão manométrica.
Comparando com o resultado da , percebemos que os valores são iguais.
Passo 4
d):
Desprezando a massa de ar que se encontra dentro do tubo, podemos calcular a massa do tubo usando o equilíbrio entre a força peso e o empuxo:
Sendo o empuxo dado por :
Passo 5
e):
Vamos usar a condição de equilíbrio novamente:
E esse é o volume ocupado pelo ar. Apenas usamos a condição de equilíbrio novamente.
Resposta
a):
b):
c):
d):
e):