P2 de Física 2- FIS1041 da PUCRIO - 2012.1

O deslocamento das partículas em uma onda sonora que se propaga no ar, cuja densidade é , é dado pela função

Através de cálculos adequados, obtenha a função da variação da pressão em função de e , não esquecendo as unidades.

Um apito emite som com frequência e move-se em uma trajetória circular de raio com uma velocidade angular de (ver figura). (Velocidade so dom no ar, )

Determine a menor e a maior frequência detectada por um observador em repouso, a uma distância do centro do círculo? Considere que o raio é muito menor do que a distância ao observador.

Suponha agora que o observador passa a se mover em direção ao apito com uma velocidade de , quais são a menor e a maior frequência detectada pelo observador?

Na figura abaixo, duas fontes sonoras e , separadas por uma distância , estão em fase e emitem ondas isotropicamente com potências e , respectivamente. Um ouvinte se encontra a uma distância da fonte , como mostra a figura. Considere a velocidade do som no ar igual a .

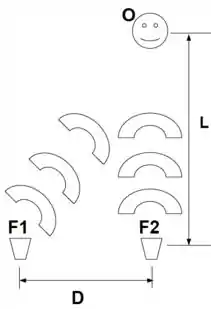
Calcule as intensidade e os níveis sonoros detectados pelo ouvinte , devidos a cada uma das fontes e , separadamente.

Com ambas as fontes ligadas, encontre a mais baixa frequência audível (ou seja, no intervalo de a ) para a qual a intensidade é mínima na posição do ouvinte.

Com ambas as fontes ligadas, encontre a mais baixa frequência audível para a qual a intensidade é máxima na posição do ouvinte.

Uma corda com de comprimento está sujeita a uma tensão de . Ela tem suas extremidade fixas e oscila em um padrão de vibrações (ondas estacionária) resultante da superposição das ondas abaixo:

sendo , e em metros e em segundos

Use o princípio de Superposição de Ondas para obter a função da onda estacionária (ou vibração estacionária) nessa corda.

A que modo normal corresponde a vibração dessa corda? Qual o número total de nós, incluindo os extremos

Desenhe o formato da corda ( versus ) para (considere as extremidade da corda em e ). Faça o mesmo para .

Determine o comprimento de onda , a frequência e a velocidade da onda , vibrando no modo fundamental.

Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A tensão na corda é e a massa específica linear . Assuma que a onda é da forma .

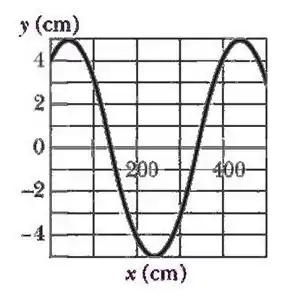
Determine a amplitude e o comprimento de onda.

Encontre a velocidade da onda, o período e o sinal que precede .

Determine a velocidade transversal máxima de uma partícula da corda.

Determine a constante de fase .

Calcule a taxa média de transporte de energia.