P3 de Física I da UFF - 2013.2

Um carrossel tem raio de e momento de inércia em relação ao seu eixo de . O carrossel está inicialmente em repouso quando uma menina de começa a caminhar sobre o carrossel com velocidade de em relação ao solo, tangente ao círculo de raio e concêntrico com o carrossel. Considere a menina como uma partícula e despreze o atrito no eixo do carrossel.

1. A partir do instante em que a meina inicia a caminhada, qual o torque resultante externo, sobre o sistema {carrossel menina}, em relação ao eixo do carrossel?
2. Calcule a velocidade angular do carrossel.
3. O que acontecerá com o carrossel se inicialmente, ao invés de caminhar na direção tangencial, a menina caminhasse em direção ao centro do carrossel (direção radial)?

No disco de e de raio são aplicadas as forças como indicadas na figura. O disco pode girar e torno do eixo que passa pelo ponto e é perpendicular ao disco.

Dados: ; ;

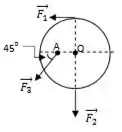
1. Calcule o torque resultante em relação ao eixo de rotação que passa em .
2. Calcule o momento de inércia do disco em relação ao eixo de rotação que passa em .
3. Calcule a aceletação angular do disco e a aceleração tangencial no ponto onde a força atua.

Um corpo de massa está preso a uma mola vertical de constante elástica de . Quando ele é puxado até abaixo do equilíbrio e largado do repouso, ele oscila com frequência de .

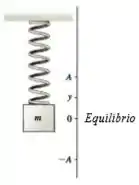
1. Determine massa do corpo.
2. Determine de quanto a mola está distendida, quando o corpo está em equilíbrio.
3. Escreva a expressão para a posição como função do tempo para o movimento oscilatório, sendo o tempo inicial quando o corpo é largado.

Dois blocos de massas e , como mostrado na figura, estão ligados por um fio e massa desprezível passando sobre uma polia de raio e massa . A polia é um disco uniforme e a corda não desliza sobre a polia. Desconsidere atrito no plano inclinado.

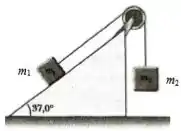
1. Desenhe o diagrama de corpo livre para cada bloco e a polia.
2. Determine a aceleração de cada bloco.
3. Determine as tensões no cabo.