Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Oscilador Linear Massa-Mola

Ver Teoria
Exercício 1412345678910111213151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

MHS

Um corpo de massa m está preso a uma mola vertical de constante elástica de 1800 N / m . Quando ele é puxado até 2,50 c m abaixo do equilíbrio e largado do repouso, ele oscila com frequência de 5 , 5 0 H z .

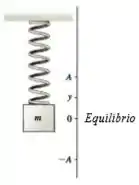
  1. Determine massa m do corpo.
  2. Determine de quanto a mola está distendida, quando o corpo está em equilíbrio.
  3. Escreva a expressão para a posição y ( t ) como função do tempo t para o movimento oscilatório, sendo o tempo inicial quando o corpo é largado.

Passo 1

Como foi visto na teoria,

ω = k m

Aplicando os valores:

2 π f = k m

2 π ∙ 5 , 5 0 2 = 1800 m

m = 1,51 k g

Passo 2

Vamos pensar juntos ao invés de aplicar a fórmula direto.

Quais forças estão atuando no corpo? Peso e força elástica. Peso pra baixo e força elástica pra cima, certo?

Então, podemos dizer que:

P = F e l

m g = k x

x = m g k

x = 1,51 ∙ 9,8 1800

x = 0,008 m = 0,8   c m

Passo 3

Bem, vamos partir do básico que sabemos:

y t = A   c o s ⁡ ( ω t + ϕ )

Como y t = - A em t = 0 , temos que ϕ = - π .

Sendo assim, sabendo o valor de ω :

y t = A   c o s ⁡ ( 34,56 t - π )

Passo 4

Agora vamos raciocinar o valor de A .

O enunciado diz que o corpo é puxado até 2,50 c m abaixo do equilíbrio. É possível que esta oscilação leve a um deslocamento maior que 2,50 c m ? Não, o movimento tende a manter tal amplitude ou diminuí-la devido à atritos e resistências.

Logo,

A = 2,5

Com isso, temos a expressão para a posição:

y t = 2,5   c o s ⁡ ( 34,56 t - π )

Resposta

  1. m = 1,51 k g
  2. x = 0,8 c m
  3. y t = 2,5   c o s ⁡ ( 34,56 t - π )

Exercícios de Livros Relacionados

Na figura, um bloco pesando 14,0N , que pode deslizar sem atrito em um plano inclinado de ângulo θ = 40,0 ° , está ligado ao alto do plano inclinado por uma mola de massa desprezível de 0,450m de comp
Um oscilador é formado por um bloco preso a uma mola ( k = 400N / m ). Em um certo instante t , a posição (medida a partir da posição de equilíbrio do sistema), a velocidade e a aceleração do bloco sã
Um bloco de 1,2k g deslizando em uma superfície horizontal sem atrito está preso a uma mola horizontal com k = 480N / m . Seja x o deslocamento do bloco a partir da posição na qual a mola se encontra
A figura mostra uma massa de 1,0k g colocada sobre uma massa de 5,0k g que oscila sobre uma superfície sem atrito. A constante elástica é de 50N / m , e o coeficiente de atrito estático entre os dois
A figura mostra um bastão homogêneo de 200g com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não