Dinâmica de Rotação
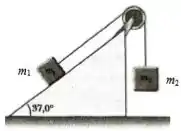
Dois blocos de massas e , como mostrado na figura, estão ligados por um fio e massa desprezível passando sobre uma polia de raio e massa . A polia é um disco uniforme e a corda não desliza sobre a polia. Desconsidere atrito no plano inclinado.
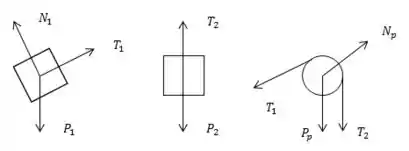
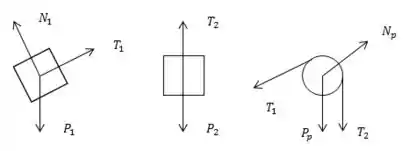
- Desenhe o diagrama de corpo livre para cada bloco e a polia.
- Determine a aceleração de cada bloco.
- Determine as tensões no cabo.
Passo 1
Essa primeira questão é mole! Matéria lá do iniciozinho do semestre. Vamos lá!
Passo 2
Apliquemos a 2ª lei de Newton, que você já está expert no assunto.
Bloco :
Bloco :
Temos 3 incógnitas para 2 equações, precisaremos trazer a polia para os cálculos. Teremos que trabalhar com rotação, visto que a polia exerce um movimento de rotação. O que vem na sua cabeça? Momento de inércia!
Polia:
Passo 3
Agora já temos 3 equações para 3 incógnitas:
Temos que:
Passo 4
Só substituir os valores no sistema.
E para tensão :
Resposta
Exercícios de Livros Relacionados
Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,