Escreva uma codificação em Matlab capaz de avaliar os valores da seguinte expansão de Maclaurin e além disso revele o erro entre a utilização da expansão e da própria exponencial.
Passo 1
Opa iae, está tudo bem?
A questão pede para elaborar um programa que calcule uma soma em séries de potência da exponencial. No caso aqui nós teremos duas entradas de dados.
A primeira entrada de dados corresponde ao número de termos que o somatório tem, no caso o , e a segunda entrada de dados é o valor de pelo qual se quer aproximar o valor da exponencial.
Porém o código deve conter uma advertência, as séries de Maclaurin foram criadas para cálculo de funções em torno da origem, ou seja, quanto mais se distanciar da origem maior será o erro.
Para elaboração desse algoritmo precisamos da função fatorial do Matlab, que sua sintaxe corresponde ao
Passo 2
Para o início do cálculo precisaremos começar pela entrada de dados:
Agora precisaremos implementar a estrutura de repetição. Para isso vamos fazer variar a expressão de controle (que é a variável que aparece ali do lado do ) de 0 até o termo N, pois o somatório acontece de 0 até N e nós vamos usar o na nossa conta. Então temos:
E repara que ali dentro do , eu já coloquei o cálculo da soma, que vai sendo alterado a cada volta, de 0 a N.
Passo 3
Uma vez que criamos o laço de repetição precisamos apenas criar a saída de dados
Além do valor da soma, vamos também criar o valor erro
Passo 4
Após a implementação do código teremos algo mais ou menos assim:
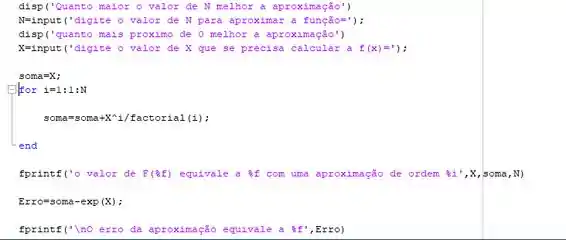
Executando o código podemos na janela command Windows teremos o seguinte resultado:

Então vemos ali na última linha que o erro é tão pequeno que o matlab aproxima pra zero.
Resposta
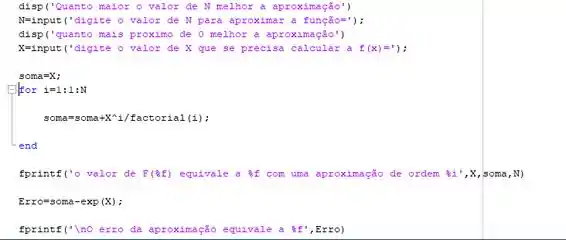
O erro é zero.