Exercícios Resolvidos de Interação, Ramificação e controle de fluxo 2(Estruturas de repetição)
Ver TeoriaEnunciado
Escreva um programa (usando os laços) que determine a soma dos primeiros termos da série.
Rode o programa com m=10 e depois com m=500.
Compare o resultado encontrado com o resultado analítico dessa soma com infinitos termos que é .
Passo 1
Opa galera, aqui temos um exercício que é laços de repetição.
Porque é um laço de repetição né?
Pelo motivo que vamos pegar a função dada no enunciado e vamos atribuir valores da seguinte forma:
E vamos conversar né? Realizar isso 50 vezes ou 500 vezes não é nada legal de se fazer.
Por isso que vamos utilizar dos laços de repetição, para assim poder realizar essa soma diversas vezes com poucas linhas de código.
Uma vez que implementamos os laços de repetição vamos comparar a soma com 50 termos desse e outra soma com 500 termos com a solução se fizéssemos infinitas vezes que é .
Sendo assim o algoritmo se comporta em 3 passos:
1-Implementação do valor de m
2-realização das estruturas de repetição
3-Análise final do resultado.
Passo 2
Agora que sabemos o que fazer primeiramente vamos implementar o número máximo da soma que vamos chamar de m, assim como a questão instruiu.
Agora vamos inserir o primeiro valor da soma, como nossa soma vai começar o então vamos colocar o elemento neutro da soma que é o 0.
Sendo assim vou dizer que a soma é:
Agora vamos criar o laço de repetição, para isso vamos utilizar a função for.
Onde o for depende de 3 argumentos, o primeiro é o valor inicial que vamos dizer que ele vai partir do ponto 1, o segundo argumento é a variação a cada repetição que também vai ser 1 e vamos finalizar com o número máximo de repetição que vai ser m.
Então o for ele vai ficar algo assim:
Inserindo a função disponibilizada na questão temos que:
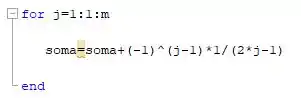
Se você escreveu tudo certinho o código deve ficar mais ou menos assim:
Passo 3
Executando o código com m=50 temos:
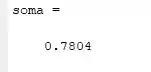
Se executarmos o código com m=500 temos:
O valor de
Logo conseguimos perceber que se aumentarmos o número de termos na soma mais próximo do valor analítico ela se aproxima.
Resposta
Ei, a resposta está no passo a passo :)