Fazer uma função que calcula a enésima potência de uma variável real x:
Passo 1
Eai, tudo beleza?
Nessa questão, vamos, inicialmente, definir o que a função vai receber como entradas, para fazer o que se pede. Para que a função calcule o valor de , precisamos quem ela tenha como entrada o e o . Vamos definir o como , pois ele pode assumir qualquer valor, e o como , pois ele é um número inteiro.
Como queremos que a função retorne , e é um , podemos definir o retorno da função como um . Com isso, temos:
![]()
Passo 2
Agora, vamos implementar o algoritmo de potenciação. Como a potenciação é a multiplicação de um número por ele mesmo vezes, vamos usar um loop. E para armazenar o produto dessas multiplicações, vamos definir uma variável , de valor inicial , que vai receber o resultado da função.
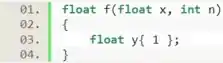
Com isso, vamos implementar o laço de para calcularmos a potenciação e armazená-la na variável . A cada iteração (volta no loop) vamos multiplicar esse produto por mais uma vez, e faremos isso vezes. Por isso, ali na linha 5, definimos que a variável de comando vai variar entre e .
Daí, dentro do , em vez de escrevermos , vamos usar o operador de atribuição por multiplicação e escrever . É um jeito mais compacto de escrever a mesma coisa.

Resposta
