A figura a seguir corresponde ao diagrama de McCabeThiele de uma mistura binária processada em uma coluna de destilação. Os valores correspondem à composição, em porcentagem da quantidade de matéria do componente mais volátil na mistura líquida () e na fase vapor ().
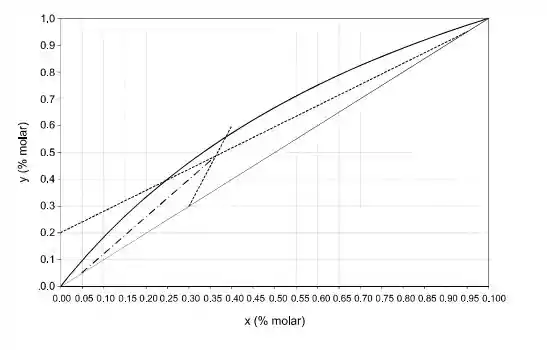
Indique as composições, em porcentagem de quantidade de matéria do componente mais volátil nas correntes de alimentação, de topo e de fundo da coluna de destilação, e a razão de refluxo no topo da coluna.
Passo 1
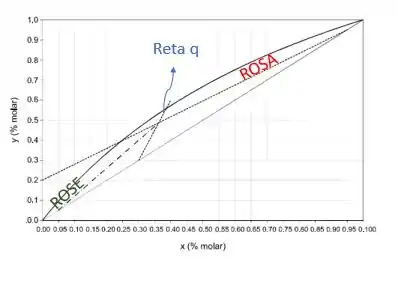
Essa questão pede várias coisas para a gente! A primeira coisa que vamos fazer é identificar o que é cada reta nesse gráfico!
Passo 2
Vamos começar avaliando o topo da nossa coluna.
Sabemos que a ROSA termina bem na composição do produto de topo, certo? Portanto, vamos efetuar a leitura dessa composição no gráfico, ok?
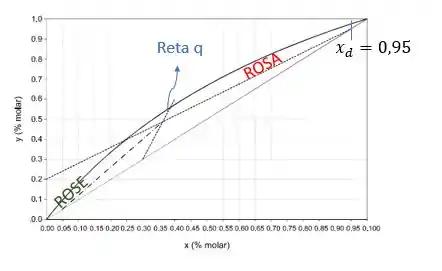
Então, o nosso produto de topo possui do componente mais leve, já que é ele que sai em maior proporção no topo!
Passo 3
Da mesma forma que podemos ver a composição de topo pelo fim da ROSA, podemos ver a composição de fundo pelo fim da ROSE.
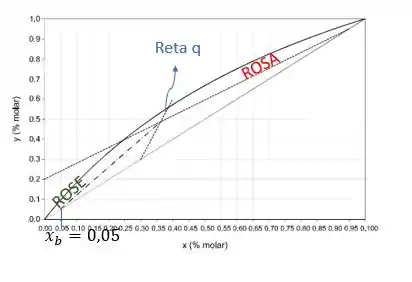
Por aí vemos que a composição do produto de fundo é , o que faz total sentido, pois o fundo é mais rico no componente mais pesado (menos volátil) e mais pobre no componente mais volátil.
Passo 4
Para saber a composição da carga, precisamos olhar para a nossa reta . O local onde a reta se inicia, ou seja, toca a diagonal , será o ponto onde veremos a composição da carga .
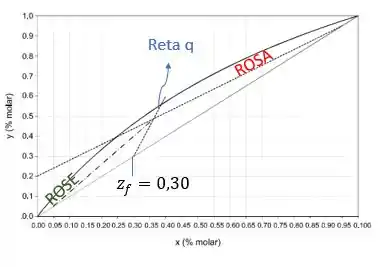
Portanto, a composição da carga é .
Passo 5
A última coisa que precisamos é determinar a razão de refluxo. E para isso, podemos usar o coeficiente linear da nossa ROSA (lembrando que ROSA é a Reta de Operação da Seção de Absorção). E nós já conhecemos a equação da ROSA:
Nesse caso, o coeficiente linear é .
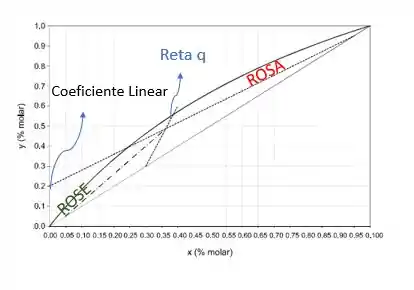
Portanto, como sabemos que , conseguimos calcular a nossa razão de refluxo, pois:
Logo, obtemos que :