Um fio de Nichrome (uma liga de níquel, cromo e ferro muito usada em elementos de aquecimento) tem de comprimento e de seção reta e conduz uma corrente de quando uma diferença de potencial de é aplicada a suas extremidades.
Calcule a condutividade do Nichrome.
Passo 1
Não fica preocupado, a condutividade (em ) nada mais é do que o inverso da resistividade (em ):
E sabemos chegar na resistividade, não é mesmo? Através dos dados do circuito! Se você não está lembrando, vem comigo...
Pra começar, vamos usar a corrente e a diferença de potencial que o problema forneceu pra calcularmos a resistência.
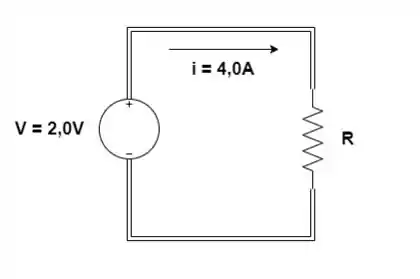
A resistência é dada por:
Onde:
Logo:
Passo 2
A resistência está associada com resistividade através da segunda Lei de Ohm:
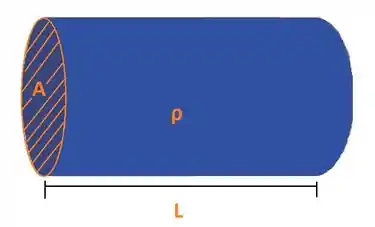
A resistência é o produto entre a resistividade e o comprimento do condutor , dividido pela área da seção do condutor !
Assim, a resistividade será:
Onde os dados no enunciado são:
Como a unidade da resistividade é Ohm-metro, precisamos passar todas as unidades para metro!
Nós já sabemos o valor da resistência que calculamos no passo anterior:
Logo:
Achamos a resistividade!
Passo 3
Finalmente, a condutividade será o inverso da resistividade: