Exercícios Resolvidos de Loops infinitos, loops aninhados e os comandos break e continue
Ver TeoriaEnunciado
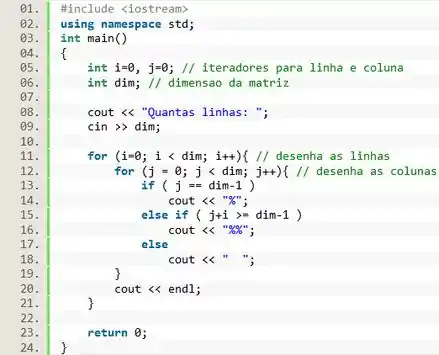
Faça um programa que desenhe na tela um triângulo utilizando somente o caractere . O usuário deve escolher a quantidade de linhas que formam o triângulo.
Exemplo, para 6 linhas:
Passo 1
Vamos lá pessoal.
A questão pede pra gente desenhar um triângulo usando o símbolo . A maior dificuldade está no fato de que esse triângulo possui a altura alinha à direita. Isso quer dizer que vamos precisar preencher vários caracteres de espaço em branco para empurrar cada um dos para o lugar certo.
Mas primeiro vamos entender como esse triângulo é formado. Note que a primeira linha possui apenas um símbolo de , a segunda linha tem três, a terceira tem cinco... ou seja, vão aumentando de dois em dois.
Vamos usar o exemplo de 6 linhas que foi dado pela questão. A gente pode imaginar esse triângulo como uma matriz, e dividir a quantidade de símbolos entre as células da matriz
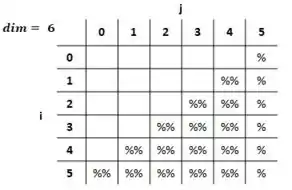
Por enquanto, não vamos nos preocupar em quantos temos em cada célula, vamos só pesar: “O que faz uma célula ser preenchida ou ficar vazia”?
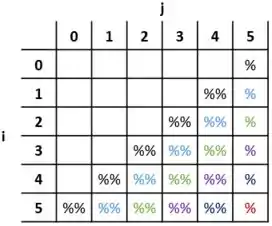
Lembrando da álgebra linear, a gente pode notar uma coisa: na diagonal secundária, a soma do é sempre constante. Não entendeu? Então olha só essa imagem:
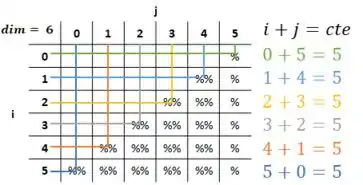
Note que o “” que obtivemos é igual a “”... e olha que show de bola, é o valor da dimensão da matriz!
E mais uma coisa interessante sobre matrizes quadradas é que esse fenômeno acontece em todas as diagonais paralelas a diagonal secundária! Olha aí em baixo uma matriz em que cada elemento é preenchido com o valor de
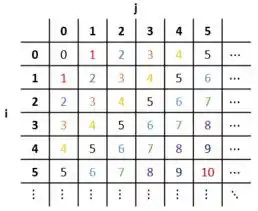
Passo 2
Então, vamos observar que:
- O valor das diagonais é constante.
- O valor da diagonal secundária é igual a
Então, pra desenhar esse triângulo, o que precisamos fazer é preencher todas as células em que seja igual ou maior a . Podemos determinar isso com uma instrução
Mas um detalhe, a última coluna é preenchida com apenas um único . Note que a posição da última coluna é igual a . Então, quando devemos escrever somente um .
Porém, como fazemos pra acessar todas as células de uma matriz? Pra isso usamos dois loops aninhados. O loop externo é responsável pelas linhas, e o loop interno é responsável pelas colunas.
Aplicando a lógica dos loops aninhados sobre a estrutura anterior vamos ter o seguinte algoritmo:
Que vai imprimir os de acordo com a seguinte lógica:
Passo 3
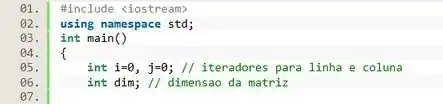
Vamos olhar agora pro algoritmo que desenvolvemos e vamos implementá-lo em linguagem C++. Pra começar escrevemos o cabeçalho e declaramos três variáveis: e para representar as linhas e colunas da nossa matriz, e a variável que determina a dimensão da matriz
Em seguida vamos receber o valor de do usuário. Pra isso vamos usar os comandos e :
Passo 4
Show, agora vamos implementar o algoritmo de fato:
Primeiro criamos um aninhamento de loops, para podermos iterar em cima da nossa matriz:
E dentro desses loops, vamos implementar a estrutura :
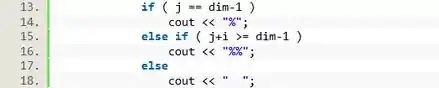
E com isso podemos fechar o loop interno e adicionar um salto de linha, depois fechamos o último loop e finalizamos o programa:
Passo 5
Passo 6
E claro, antes de terminar precisamos testar o programa:
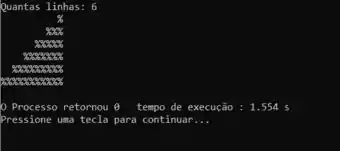
E prontinho! Finalizamos essa questão super da hora!
Resposta
