Aplicação método das forças – Temperatura
Produzido por Pablo RicardoTeoria
Introdução
Para cálculo dos esforços devido a temperatura, basta pensarmos que na verdade a temperatura é um carregamento do sistema zero, e ai que entra a jogada, no sistema zero, temos uma estrutura isostática carregada ou com temperatura, e nesse caso, sabemos que em estruturas isostáticas, obrigatoriamente, os digramas de momento, cortante e normal devido a temperatura são zero, o que facilita a nossa conta.
Algo que também é importante é que se você estiver em uma questão com itens a) , b) e c) em que no item a) você avalie um carregamento, no b) a temperatura e no c) o recalque, você não precisara calcular tudo de novo, aqui em baixo eu vou dar esse resuminho:
- As deformações , e você vai ter que calcular em cada item, tanto na a) quanto no b) quanto no c)
- As deformações , , todos esses você só calcula uma vez, ou seja, ao fazer o item a) você já determinou o sistema que será usado no b) e no c) , faltando definir, é claro, somente o que definimos aqui em cima.
Em resumo, se nosso sistema for
O que está em vermelho vai ser definido em cada um dos itens (a, b e c). o que está em verde serão as incógnitas de cada um do ítens, então também vão ser definidos dependendo se estamos no a, b ou c. porém tudo que está em preto será determinado apenas uma vez.
Entendida essa introdução, vamos ver como aplicar ao nosso problema a temperatura.
Temperatura
Imagine agora que no item b) pedisse que você analisasse a mesma estrutura, porém tendo as fibras superiores e inferiores com uma diferença de temperatura de 10°C (em que as fibras internas tivessem a maior temperatura e as externas a menor, ou seja, a variação de temperatura é positiva) com uma altura de seção de 1m e .
A primeiríssima coisa que você já pode fazer é garantir metade do seu sistema, ou seja, como é a mesma estrutura, eu já sei com certeza que:
Ou seja, não preciso me preocupar com nada do hiperestático, mas ainda preciso determinar o valor de , e para isso podemos seguir o passo a passo para variação de temperatura em sistemas isostáticos.
sabemos que para cálculo da temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico, podemos descartar a contribuição de normais, e ficar apenas com a contribuição de momentos fletores. Dessa maneira teremos que a nossa fórmula será.
Sabemos que a variação de temperatura, a altura e o coeficiente de dilatação térmicos são constantes na nossa equação, logo podemos escrever a mesma da seguinte maneira.
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S de cada barra, nada mais é que a área do diagrama, ou seja, nossa fórmula passa a ser.
Em que:
Mas onde está essa carga unitária? Usamos exatamente o mesmo princípio do recalque. Posicionamos a carga unitária no mesmo ponto, na mesma direção e no mesmo sentido que o hiperestático está. E nesse caso como precisamos da área do diagrama de momentos fletores, basta apenas determinar as áreas e somar elas. Assim teremos:
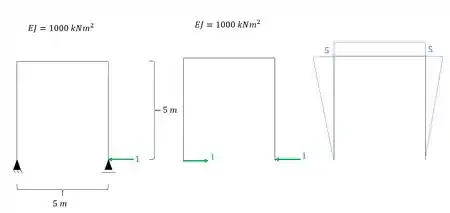
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LEMBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
- Sempre confira os valores de , , pois apesar deles serem calculados uma única vez, se for calculado uma única vez errado, você erra a questão inteira, então sempre tome bastante cuidado.
- Sempre reaproveite sistemas que você já estive feito, perceba que o sistema hiperestático sempre vai fornecer o diagrama e as reações de apoio que vamos precisar para calcular as deformações zeros, tanto para recalque quanto para temperatura.
- E exercite bastante para você pegar todos os macetes.
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Assim teremos:
E perceba que a área deu negativa pois as fibras tracionadas são as externas.
Substituindo teremos que:
E quem é essa deformação? Exatamente o nosso . Substituindo no sistema teremos que:
E assim conseguimos determinar qualquer esforço na estrutura a partir de .
Perceba que a aplicação é bem tranquila, mas é preciso tomar bastante cuidado, então vou dar umas dicas aqui.
Então chega de ladainha e vamos exercitar!!!
Temperatura
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Determine as reações de apoio de um pórtico que suas fibras externas estão a uma temperatura de 40°C e as fibras internas estão a uma temperatura de 10°C.
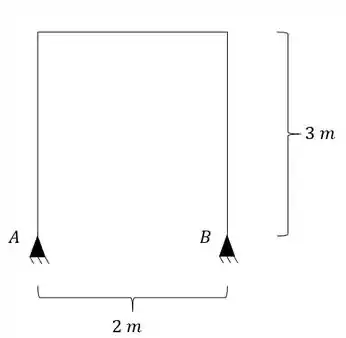
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do segundo gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
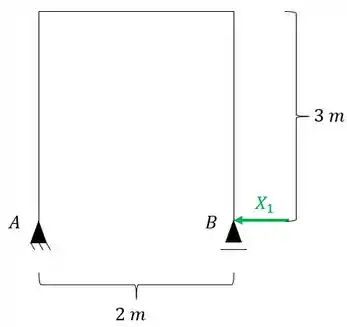
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é variação de temperatura, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de temperatura. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
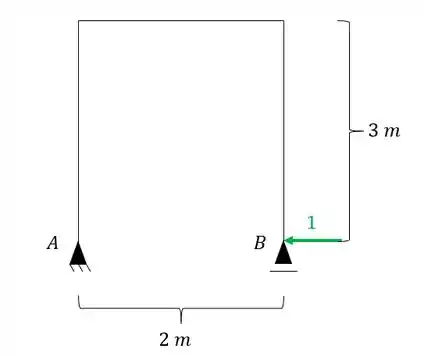
sabemos que para cálculo da deformação pela temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico devemos considerar ambas as contribuições. Mas podemos simplificar como:
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, assim como o normal, nada mais são que as áreas dos respectivos diagramas, ou seja, nossa fórmula passa a ser.
Em que:
Como sabemos, iremos usar exatamente a carga unitária na mesma posição do hiperestático. Dessa maneira teremos que:
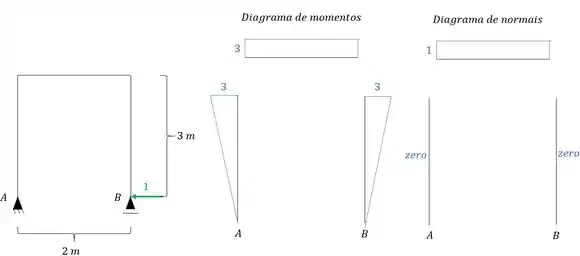
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as aréas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Sabemos também que:
e por fim determinamos o valor de que será dado por:
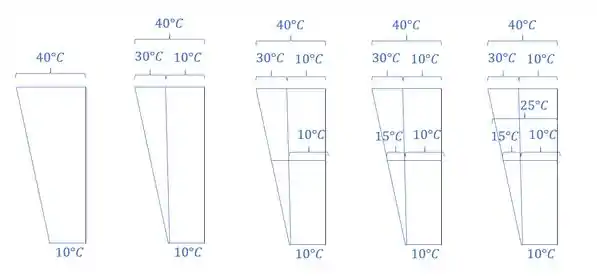
E fizemos isso porque sabemos que em seções retangulares o centro de gravidade é no meio do retângulo.
Sendo assim teremos que:
Substituindo na equação teremos que:
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
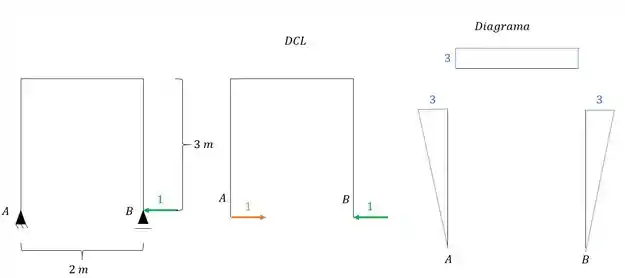
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
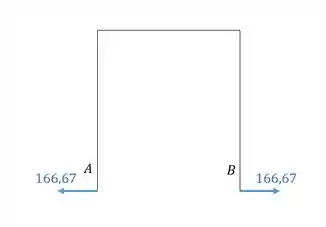
Como só temos reações horizontais, as nossas reações serão.

Resposta
Reações horizontais de apoio
Exercício Resolvido #2
Origem do Exercício
Determine as reações de apoio de um pórtico que suas fibras externas estão a uma temperatura de -50°C e as fibras internas estão a uma temperatura de 150°C.
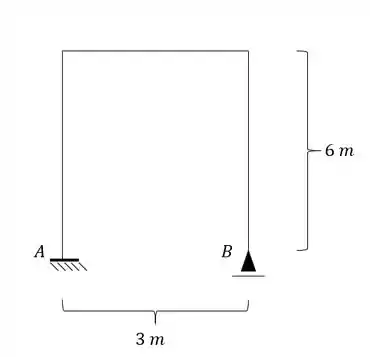
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 1 apoio do terceiro gênero e um apoio do primeiro gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
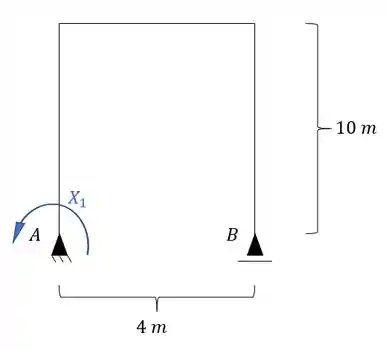
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é uma variação de temperatura, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de temperatura. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
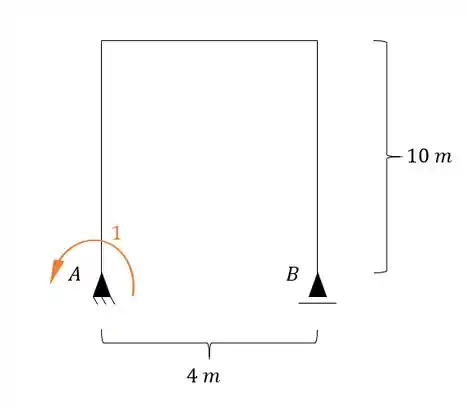
sabemos que para cálculo da deformação pela temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico devemos considerar ambas as contribuições. Mas podemos simplificar como:
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, assim como o normal, nada mais são que as áreas dos respectivos diagramas, ou seja, nossa fórmula passa a ser.
Em que:
Como sabemos, iremos usar exatamente a carga unitária na mesma posição do hiperestático. Dessa maneira teremos que:
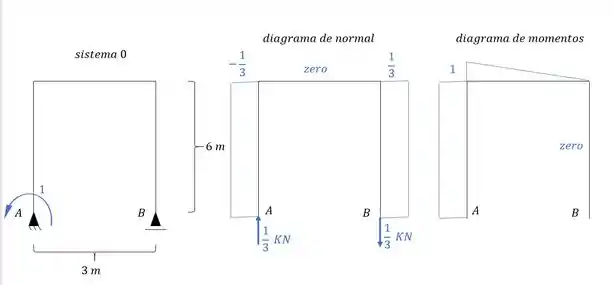
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as aréas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Sabemos também que:
e por fim determinamos o valor de que será dado por:
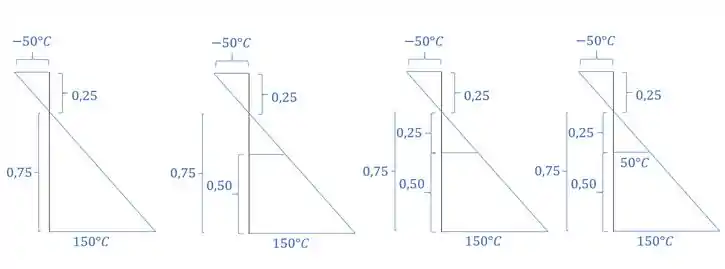
E fizemos isso porque sabemos que em seções retangulares o centro de gravidade é no meio do retângulo.
Sendo assim teremos que:
Substituindo na equação teremos que:
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
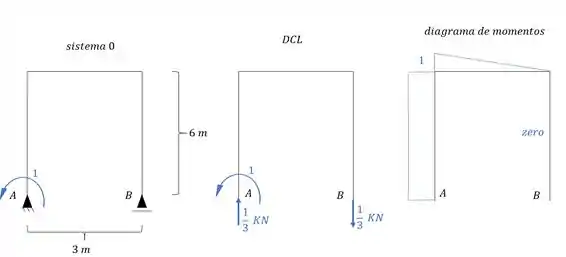
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Determinando as reações de apoio teremos que:
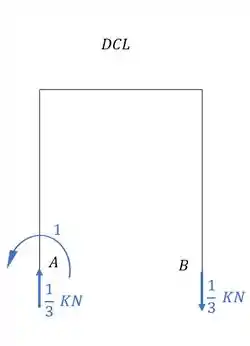
Vale lembrar que em estruturas isostáticas, tanto a variação de temperatura quanto o recalque produzem reações de apoio idênticas a zero, sendo assim sempre iremos zerar o primeiro termo.
e já sabemos que:
Resposta
Exercício Resolvido #3
Elaboração própria
Determine as reações de apoio de um pórtico que suas fibras externas estão a uma temperatura de 0°C e as fibras internas estão a uma temperatura de 80°C.
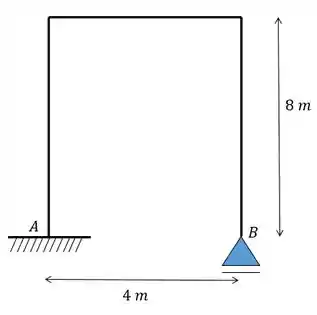
Passo 1
Fala pessoal!! agora vamos resolver um exercício que trata sobre a influência da temperatura nos pórticos. Para achar as reações dos apoios como o problema pede e resolver essa questão a gente precisa primeiro dividir essa estrutura numa estrutura isostática.
Depois de fazer essa divisão nós vamos calcular o deslocamento imposto pela temperatura e finalmente achar o hiperestático, de forma a calcular as reações. Então partiu!
Passo 2
Quebrando essa estrutura de forma a obter uma estrutura isostática vamos ter.
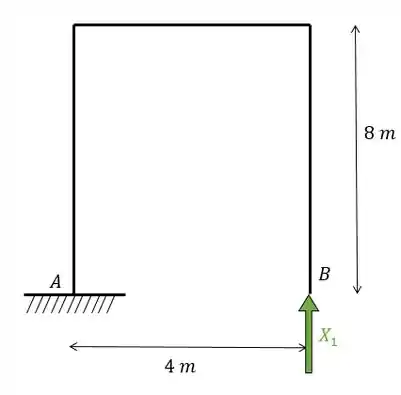
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é uma variação de temperatura, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de temperatura. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 3
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
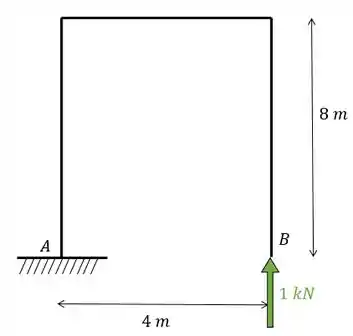
sabemos que para cálculo da deformação pela temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico devemos considerar ambas as contribuições. Mas podemos simplificar como:
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, assim como o normal, nada mais são que as áreas dos respectivos diagramas, ou seja, nossa fórmula passa a ser.
Em que:
Como sabemos, iremos usar exatamente a carga unitária na mesma posição do hiperestático. Dessa maneira teremos que:
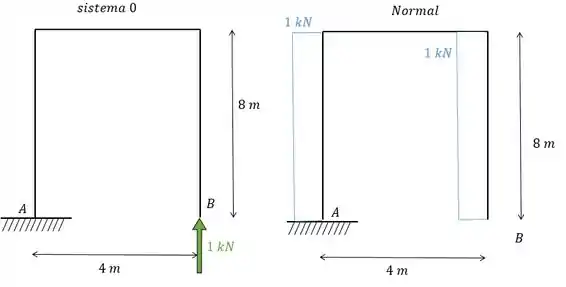
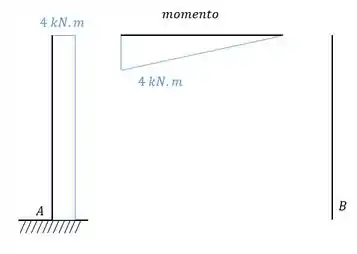
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as aréas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Passo 4
Agora vamos partir para a parte da temperatura.
Sabemos também que:
e por fim determinamos o valor de que será dado pela média simples dado que a geometria é regular
Substituindo na equação teremos que:
Passo 5
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
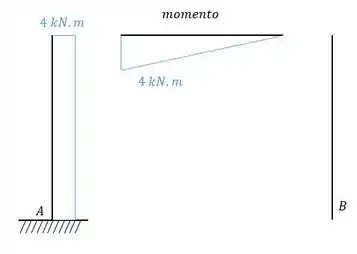
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Passo 6
Determinando as reações de apoio teremos que:
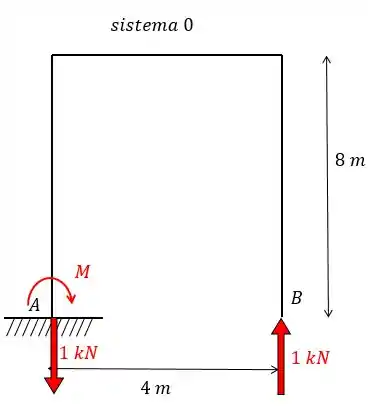
Vale lembrar que em estruturas isostáticas, tanto a variação de temperatura quanto o recalque produzem reações de apoio idênticas a zero, sendo assim sempre iremos zerar o primeiro termo.
Para o momento
Resposta
Exercício Resolvido #4
Origem do Exercício
Determine as reações de apoio do pórtico abaixo, sabendo que o mesmo sofre um recalque vertical para baixo de 5cm no apoio A. E no apoio B, ainda sofre um recalque de 10 cm pra cima e 3 cm para direita.
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 2 apoios do segundo gênero, totalizando 4 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
Ou seja, nossa estrutura possui um grau de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando um vinculo teremos a seguinte nova estrutura.
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é um recalque de apoio, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de recalque. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
Para esse sistema como definimos a deformação quando estamos vendo o recalque? Não seria exatamente calculando as reações de apoio, e usando a nossa formulazinha?
Determinando as reações de apoio desse sistema teremos que:
E como eu disse, precisamos relacionar as reações de apoio com seus respectivos recalques, que nesse caso será dado por.
Como o 4cm não tem par, só iremos ter dois termos.
E antes de substituirmos na fórmula precisamos saber como funciona o esquema de sinais.
- Sinais
Sempre que a reação for no mesmo sentido do recalque, ela será positiva,
e sempre que for no sentido contrário, será negativa.
Por fim, o último passo é substituirmos na nossa fórmula, que será dada por:
Sabe quem é essa deformação? É exatamente o nosso , então podemos escrever ele como.
Passo 3
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Como só tivemos reações horizontais sabemos que as reações serão dadas por:
Resposta
Reações horizontais de apoio
Exercício Resolvido #5
Origem do Exercício
Determine as reações de apoio de um pórtico que suas fibras externas estão a uma temperatura de -50°C e as fibras internas estão a uma temperatura de 50°C.
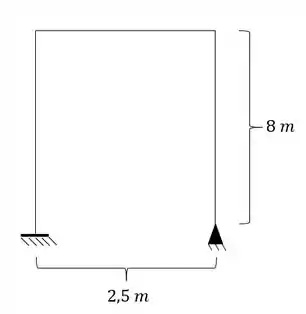
Passo 1
Sabemos que a primeira coisa que devemos fazer é determinar o número de hiperestáticos.
- Hiperestáticos totais pelo macete
- Sabemos que temos 1 apoio do terceiro gênero e um apoio do segundo gênero, totalizando 5 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
- para o sistema 10 será
Ou seja, nossa estrutura possui dois graus de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática.
Quebrando dois vínculos quaisquer teremos a seguinte nova estrutura.
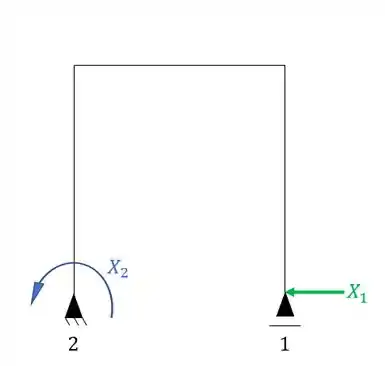
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é uma variação de temperatura, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de temperatura. Parece meio embolado, mas é bem tranquilo, me segue aqui.
Passo 2
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático. Mas o que vai acontecer quando temos 2 hiperestáticos? Todos os exercícios que vimos até aqui só tinham 1 grau de hiperestaticidade, então só ia ter um sistema zero. Aqui vamos ter 2 sistemas zeros! Então pra não causar confusão e combinar a nomenclatura com as das deformações, vamos nomear eles de 10 e 20.
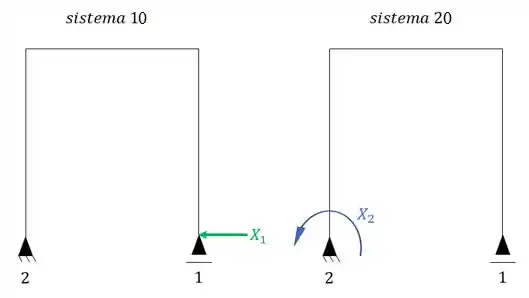
sabemos que para cálculo da deformação pela temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico devemos considerar ambas as contribuições. Mas podemos simplificar como:
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, assim como o normal, nada mais são que as áreas dos respectivos diagramas, ou seja, nossa fórmula passa a ser.
Em que:
Como sabemos, iremos usar exatamente a carga unitária na mesma posição do hiperestático. Dessa maneira teremos que:
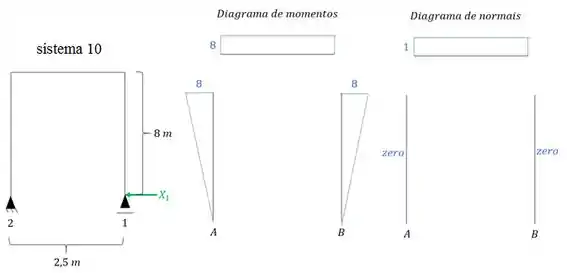
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as áreas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
- para o sistema 20 será
- NORMAIS
- MOMENTOS FLETORES
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Sabemos também que:
e por fim determinamos o valor de que será dado por:
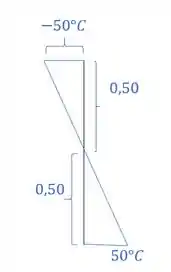
E fizemos isso porque sabemos que em seções retangulares o centro de gravidade é no meio do retângulo.
Sendo assim teremos que:
Substituindo na equação teremos que:
Passo 3
Lembre-se que também temos que calcular o valor de , que será calculado da mesma maneira que calculamos anteriormente.
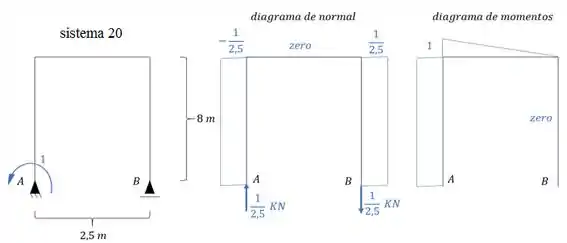
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as aréas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Sabemos também que:
e por fim determinamos o valor de que será dado por:
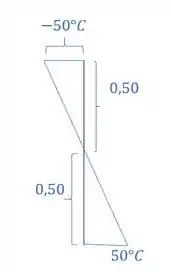
E fizemos isso porque sabemos que em seções retangulares o centro de gravidade é no meio do retângulo.
Sendo assim teremos que:
Substituindo na equação teremos que:
Passo 4
Agora precisamos calcular os deslocamentos referentes a estrutura em si, dessa maneira teremos que fazer as combinações dos diagramas de momentos entre si, dessa maneira teremos que:
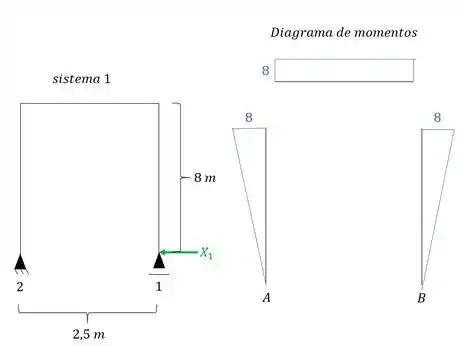
Como , teremos que
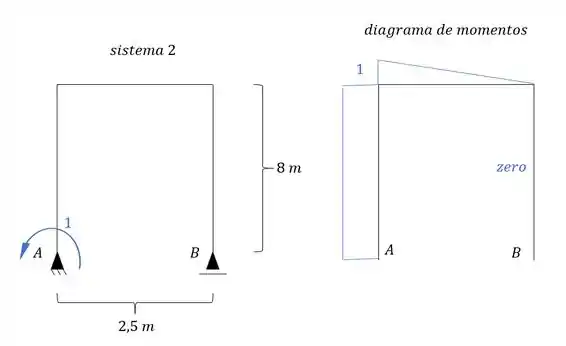
Como , teremos que
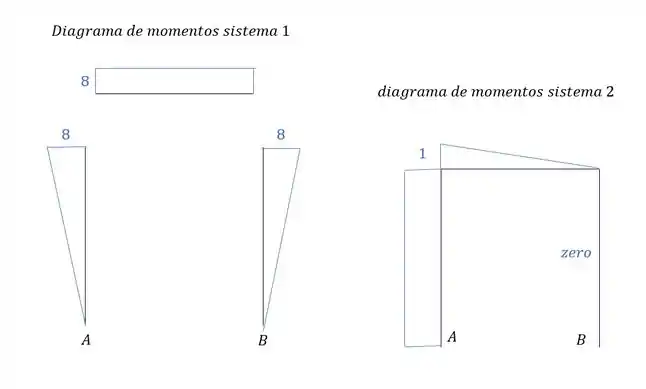
Como , teremos que
Passo 2
E assim teremos que o nosso sistema será:
Substituindo teremos que
Para facilitar a solução do sistema podemos multiplicar todos os termos por EJ, sendo assim teremos o novo sistema sendo:
E como do outro lado é zero podemos descartar esse EJ, sendo assim teremos que
Agora só precisamos lembrar que para determinar as reações de apoio precisamos analisar as reações calculadas em cada sistema, e lembrar que no sistema zero apenas com ação da temperatura não haverá reações de apoio.
Determinando as reações de apoio teremos que:
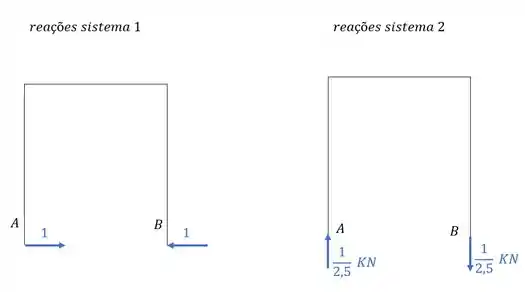
e já sabemos que: