Método de Williot – Recalque do apoio
Produzido por Pablo RicardoTeoria
Introdução
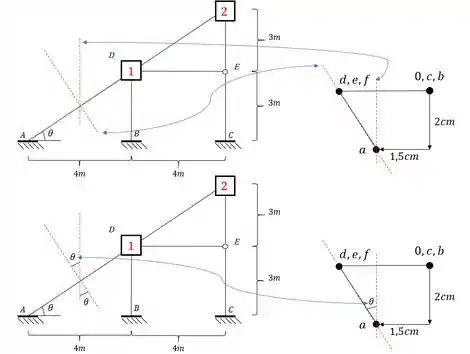
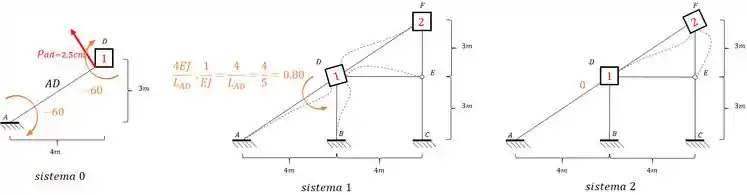
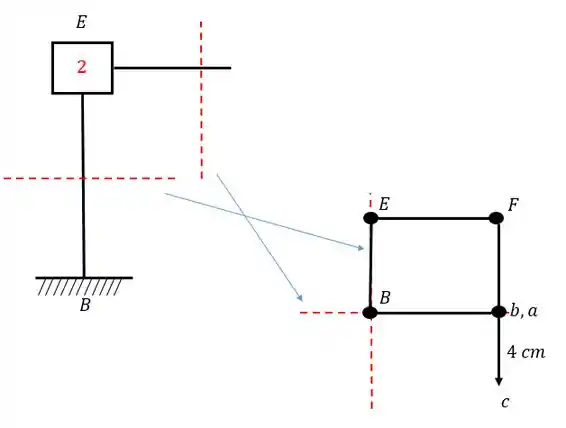
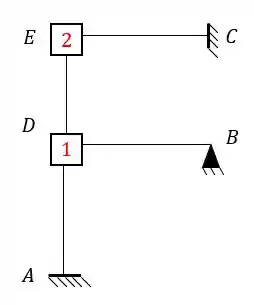
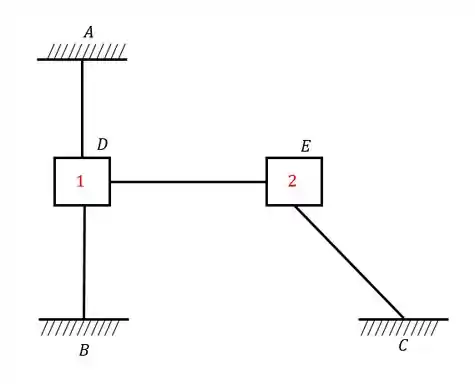
Assim como aprendemos no método das forças a resolver problemas com recalque de apoio, também vamos aprender a fazer isso no método dos deslocamentos usando o conceito de williot. Como é mais fácil entender em um exemplo pratico do que em um exemplo teórico, imagine que temos a seguinte estrutura:
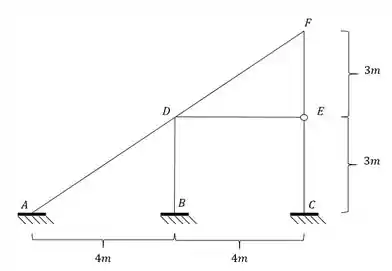
E imagine que o ponto A da nossa estrutura recalcou 1,5 cm para esquerda e 2cm para baixo. Sabendo isso determine a rotação dos pontos D e F da nossa estrutura. Use .
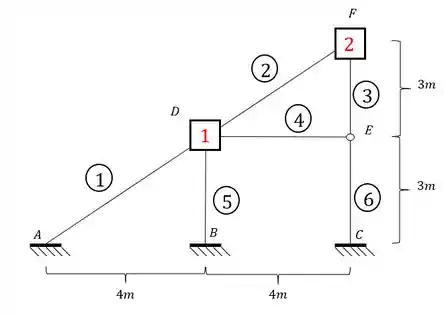
Passo 1 – determinação das deslocabilidades
Como vimos bastante isso nas aulas passadas, não vamos nos aprofundar nisso aqui nessa aula. Então já indo direto ao ponto temos que:
- Não possuímos deslocabilidades externas
- As deslocabilidades internas são os nós que não são apoio extremos, apoios normais e nem rótulas, ou seja, no nosso caso os nós D e F.
- E todo nó com deslocabilidade interna nós colocamos uma chapa.
Dessa maneira temos que:
Passo 2 – usando o método de Williot
O método de Williot, de início pode dar uma confundida, mas vamos passo a passo para ficar bem tranquilo, perceba que vamos representar os nós das barras com letras minúsculas, apenas para não confundir.
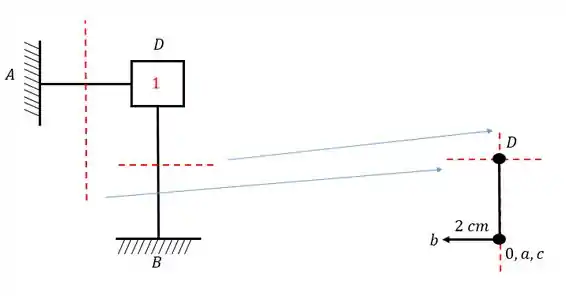
- Primeiro passo – definir uma origem
- Segundo passo – achar o ponto que recalca
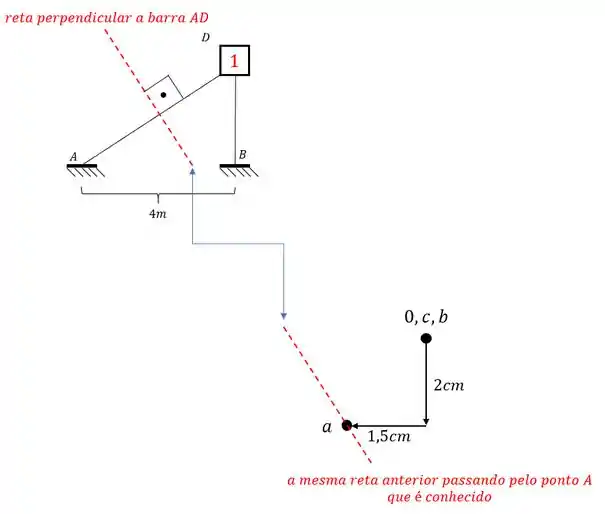
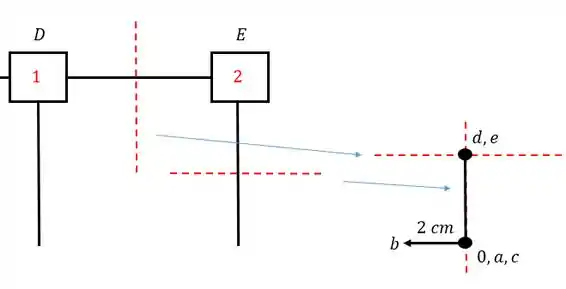
- Terceiro passo – Determinar o próximo ponto em função dos que já temos, por exemplo o ponto D
- Perceba que temos o ponto A e o ponto B, logo conseguimos chegar no ponto D, para isso precisamos ver o seguinte.
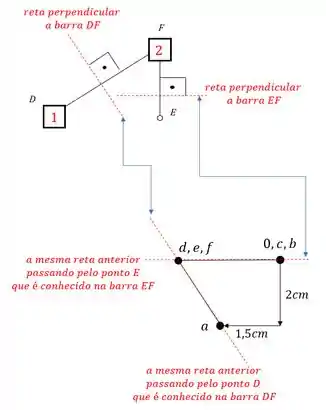
- Traçamos uma reta perpendicular a barra AD ( barra que possui o ponto A conhecido e o ponto D a ser conhecido), e essa reta perpendicular fazemos passar pelo ponto A do williot (porque o ponto A do williot é o ponto que conhecemos da nossa barra AD), sendo assim teremos:
- Mas veja que o ponto A sozinho não pode determinar D, para isso precisamos também do ponto B, e no caso da barra BD. E o processo é exatamente o mesmo. Traçamos uma reta perpendicular a reta BD, e fazemos essa reta passar pelo ponto conhecido do williot, que nesse caso é ponto D, sendo assim teremos que:
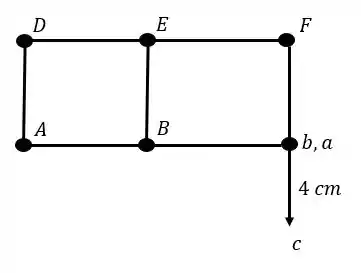
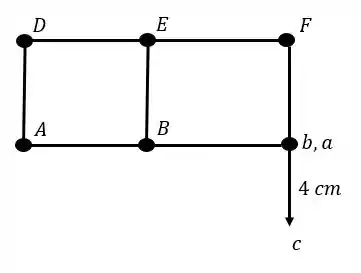
- Quarto passo – Determinar o próximo ponto em função dos que já temos, por exemplo o ponto E e F.
- Quinto passo – determinado os pontos determinamos as distancias entre eles, e com isso basta usarmos os valores que já temos (lembre-se que como usamos retas perpendiculares as barras da estrutura, que já conhecemos, conseguimos facilmente determinar também os ângulos do williot, sendo assim teremos que:
- Primeiro : como nomear as barras.
Isso é bem importante, porque essa definição vai dizer como devemos olhar o nosso williot, e em que ponto devemos aplicar o nosso deslocamento.
As nossas barras sempre serão nomeadas na ordem em que os pontos que compõem elas foram determinados, por exemplo:
- barra AD
- Barra FD
- Sabemos que primeiro determinamos o Ponto A e depois o D, ou seja, o deslocamento da nossa barra se dará de A para D.
ela deve ser nomeada como AD mesmo porque primeiro determinamos o ponto A e depois o ponto D no williot.
Quem nós determinamos primeiro? O D ou o F? o D, certo? Então a nomeação dessa barra na verdade deve ser DF.
E assim repetimos para todas as barras.
E porque fazemos isso? Muito simples, imagine que queremos saber o deslocamento da barra AD.
- Obs: se você prestar a atenção ali em cima, nenhuma das nossas barras possui a chapa 2 junto com um deslocamento, o que isso significa? Que todos os possíveis deslocamentos que poderiam causar momentos na chapa 2, são zeros, ou seja:
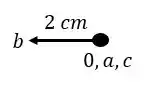
A origem vai ser definida por um ponto 0, e junto com essa origem vamos por todos os pontos que são naturalmente indeslocaveis (no nosso exemplo esses pontos são dados pelos engastes B e C, mas tome cuidado porque o engaste A também seria, PORÉM, ele é o apoio que recalca, então por isso ele deixou de ser indeslocavel. Então vamos marcar esse primeiro ponto.
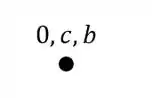
Esse ponto também é bem fácil de determinar, porque é exatamente fazer os deslocamentos que o enunciado nos dá, e o final desses deslocamentos é exatamente o nosso ponto deslocado, que no nosso exemplo é o ponto A, sendo assim temos que:
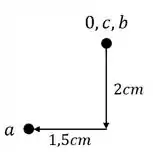
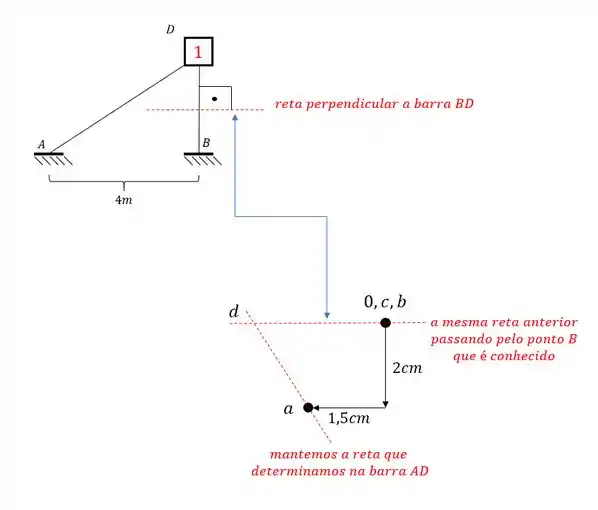
Perceba que o ponto de encontro das duas retas perpendiculares a AD e BD é exatamente o nosso ponto D.
Vamos seguir o mesmo padrão. Precisamos achar o ponto E no williot. Sabemos que os pontos D e C estão no nosso williot. E as retas que ligam esses pontos ao ponto E são as retas DE e CE, sendo assim teremos:
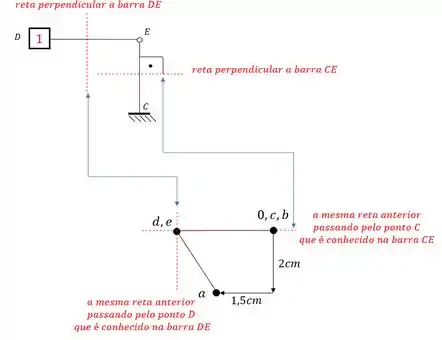
E perceba que assim conseguimos determinar o ponto E do nosso williot. E para o ponto F teremos o mesmo cálculo dado por:
E veja que podemos dizer que:
Agora fica fácil determinar as medidas:
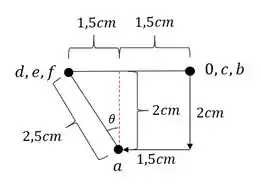
Passo 3 – Determinando e
Perceba que no nosso caso, os nossos nós vão estar sendo deslocados, ou seja, quando ocorrer o recalque do apoio, os nós na realidade irão sofrer um deslocamento, e descobrimos que para determinar os momentos na nossa chapa, devido a deslocamentos, devemos usar a seguinte equação da nossa tabela:
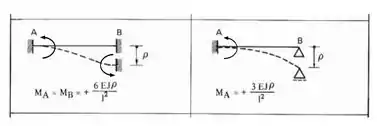
E é aqui que entra o nosso williot, ele vai nos ajudar a determinar o deslocamento relativo de cada barra, esse deslocamento vai ser o nosso , e com isso vamos poder substituir esse valor na nossa fórmula, então vamos olhar como determinar esses nas nossas barras.
Passo 4 – Determinando
Isso é muito simples, para determinarmos o deslocamento de uma barra precisamos primeiro determinar de que ponto para que ponto a nossa barra deslocou, usando o gráfico do williot, e depois determinar esse deslocamento nas barras da estrutura principal. Pode parecer meio complicado, mas vamos aos pouquinhos pra entender:
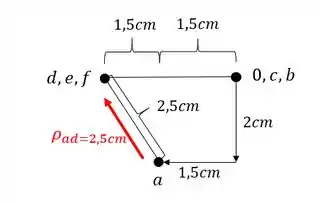
E onde aplicamos esse deslocamento? No ponto A ou no ponto D? é ai que entra a segunda vantagem da nossa nomeação. O deslocamento sempre será aplicado no segundo termo do nome da nossa barra. Ou seja, se a barra renomeada é AD, então aplicamos o deslocamento no ponto D. sendo assim os deslocamentos de todas as nossas barras serão dadas aqui embaixo. Perceba que primeiro vamos dar a nossa barra com o nome certinho. Depois vams dar o deslocamento no williot e por fim vamos dar o ponto em que devemos aplicar.
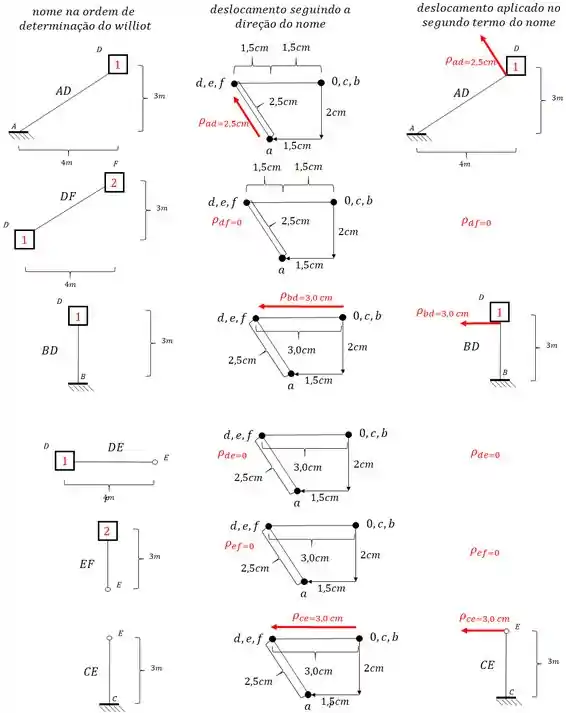
Passo 5 – enfim os valores e
Lembra que nosso objetivo era determinar e ? Para isso basta alinharmos todos os momentos que agem tanto na chapa 1 quanto na chapa 2, ou seja, das nossas barras acima que possuem deslocamento diferente de zero, vamos separar apenas as que possuírem as chapas (lembrando que as chapas representam engastes).
Definido isso, vale lembrar que não significa que sempre , isso ocorreu no nosso exemplo apenas.
Mas prosseguindo, temos que as duas barras com a chapa 1 e com deslocamento são:
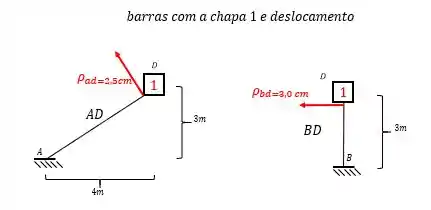
Perceba que ambas têm um engaste na ponta, e na outra a chapa, e como sabemos que a chapa representa um engaste, podemos dizer que as nossas barras são Bi-engastadas.
Com isso, se temos um deslocamento, e as barras são biengastadas, devemos usar a seguinte equação:
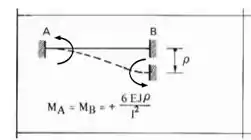
Que nas nossas barras produzirá:
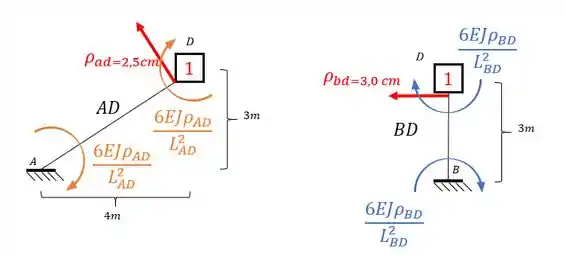
Com isso podemos dizer que os momentos que agem na chapa 1 são:
Desses valores temos que:
Passo 6 – Determinando os valores , ,
Esses aqui já são nossos velhos conhecidos de muita dor de cabeça. Já vimos nas aulas anteriores que para determinarmos eles, basta que rotacionemos as chapas da nossa estrutura e usemos a tabela abaixo para determinação dos valores.
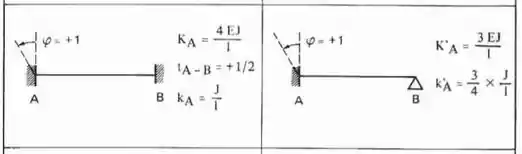
Não vamos nos aprofundar nisso aqui porque já vimos bastante nas nossas ultimas aulas. Dessa maneira teremos que:
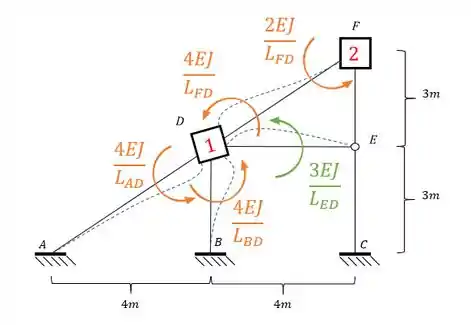
Usando como fator para rigidez relativa:
E para barra 2 temos que:
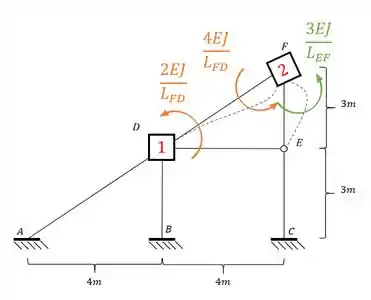
Usando como fator para rigidez relativa:
No nosso sistema temos que:
Substituindo:
Assim teremos que:
Vamos calcular o momento por exemplo na barra AD, no ponto D, fazendo isso vamos ter que:
Passo 2 – usando o método de Williot
Passo 3 – Determinando β 10 e β 20
Passo 4 – Determinando o s ρ ' s
Passo 5 – enfim os valores β 10 e β 20
Passo 6 – Determinando os valores β 1 1 , β 2 2 , β 12 , β 21
Exercícios Resolvidos
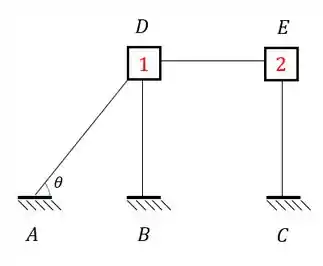
Exercício Resolvido #1
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio B recalca 3cm para baixo.
Passo 1
Agora já podemos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são A e C. mas porque não o B? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros dois.
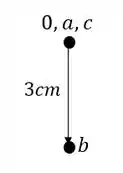
Passo 2
Em seguida, através dos recalques, marcamos a posição final dos pontos que deslocaram, dessa maneira teremos que, como o ponto B apenas desceu, teremos que a sua marcação será:
Passo 3
Agora precisamos determinar os pontos seguintes a partir dos pontos que já temos.
Por exemplo, o ponto D, pode ser determinado a partir dos pontos A e B do Wiiliot, lembrando que sempre usamos no williot os eixos perpendiculares as barras analisadas. Dessa maneira teremos que:
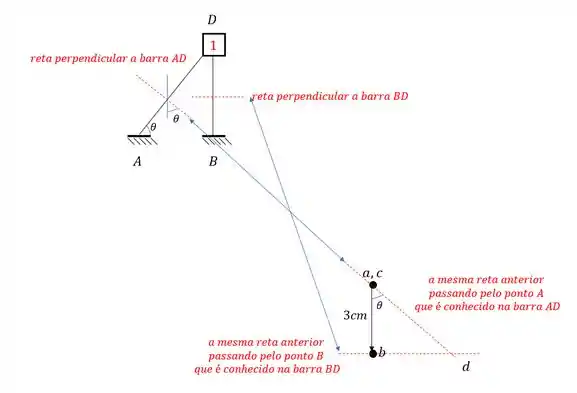
e assim determinamos o nosso ponto D, e perceba que também aproveitamos e já deixamos o ângulo pronto para o caso de ser necessário usar ele.
Passo 4
Agora, por fim, o ponto E, pode ser determinado a partir dos pontos D e C do Wiiliot, lembrando que sempre usamos no williot os eixos perpendiculares as barras analisadas. Dessa maneira teremos que:
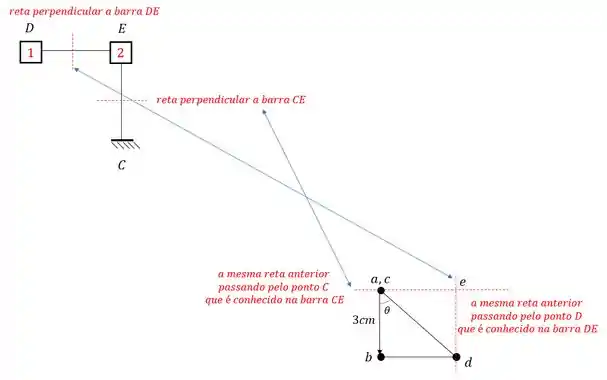
e assim determinamos o nosso ponto E. e concluímos o nosso williot.
Perceba que se tivermos o valor de , iremos conseguir determinar todas as medidas que faltam. Mas o que é importante mostrar é que estruturalmente determinamos tranquilamente o nosso williot, e que, com o valor do ângulo, conseguimos determinar qualquer medida.
Assim nosso williot final será.
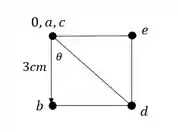
Resposta
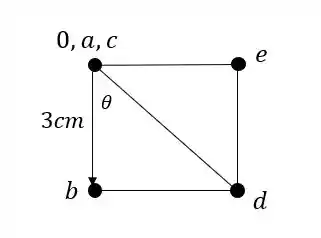
Exercício Resolvido #2
Elaboração própria
Determine o Williot da estrutura abaixo, sabendo que o apoio C recalca para baixo.
Passo 1
Vamos lá, pessoal!! Vamos achar o Williot dessa estrutura com o determinado recalque. Como e estão engastados, então são apoios indeslocáveis enquanto o apoio por mais que também esteja engastado irá sofrer um recalque, logo, é deslocável.
Dessa forma a gente vai começar pelo nosso pontinho representando os três engastes:
![]()
Passo 2
Agora vamos marcar o deslocamento do nosso pontinho, que foi um recalque de para baixo:
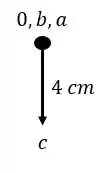
Passo 3
Agora chegou a hora da gente achar os outros pontos. Vamos fazer isso a partir do nosso pontinho já determinado e utilizando eixos perpendiculares às barras. Para o ponto nós vamos ter:
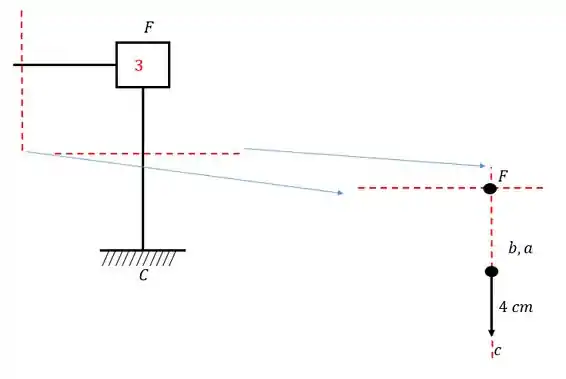
Passo 4
Da mesma forma vamos fazer para os próximos pontos:
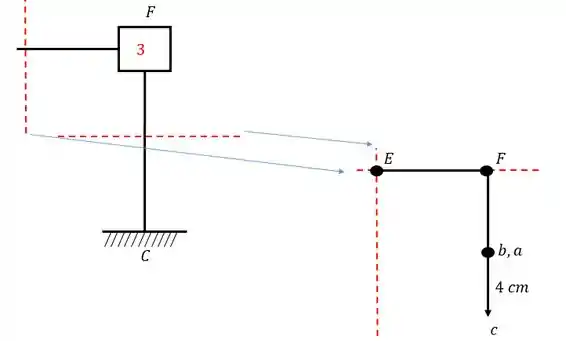
Passo 5
Perceba que a gente constrói o ponto seguinte com base no ponto anterior e nas direções das barras. Agora para vamos ter:
Passo 6
Agora faltam só os pontos e que podemos completar, como serão muito parecidos com os pontos e vamos só fazer a mesma coisa e resulta em:
E essa é a nossa resposta!
Resposta
Exercício Resolvido #3
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio A recalca 4cm para baixo e 2 cm para direita.
Passo 1
Vamos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são B e C. mas porque não o A? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros dois.
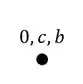
Lembre-se de sempre representar com letras minúsculas.
Passo 2
Em seguida devemos marcar a partir da origem o ponto que se deslocou, que no nosso caso foi o ponto A, que foi 4cm pra baixo e 2cm pra direita.
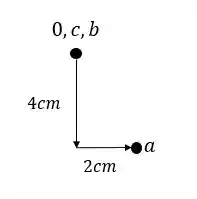
Passo 3
E agora o mais difícil que seria o ponto D.
Para determinar ele, precisamos usar a nossa regrinha básica. Escolhemos dois nós que nos auxiliem a achar o ponto D.
Podemos usar por exemplo os pontos B e A.
Devemos passar uma reta perpendicular a essas barras, e transferir elas pro nosso williot, sendo assim teremos que:
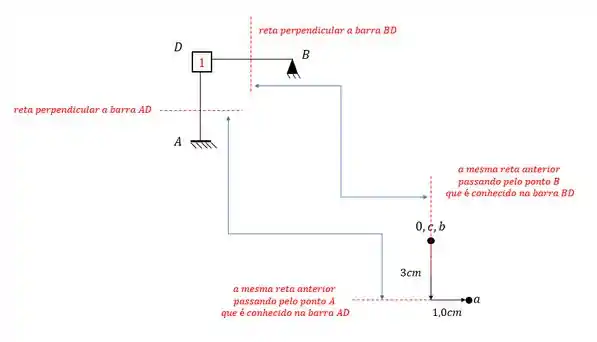
O ponto de encontro das retas é exatamente o nosso ponto D.
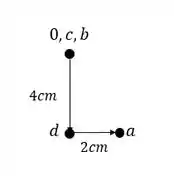
Passo 4
Para determinar o ponto E devemos usar os pontos C e D, sendo assim teremos que:
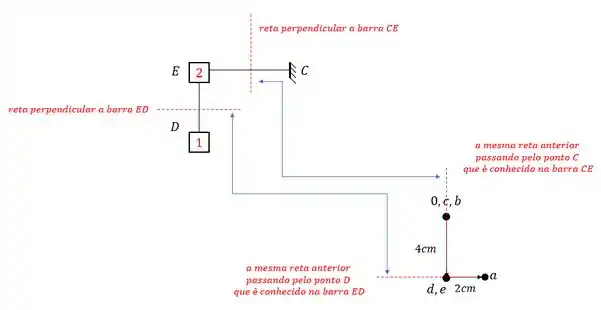
E vemos que nesse caso o ponto E coincide com o ponto D.
Assim nosso williot será.
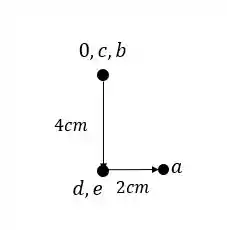
Resposta
Exercício Resolvido #4
Elaboração própria
Determine o Williot da estrutura abaixo, sabendo que o apoio sofre um recalque de para a esquerda.
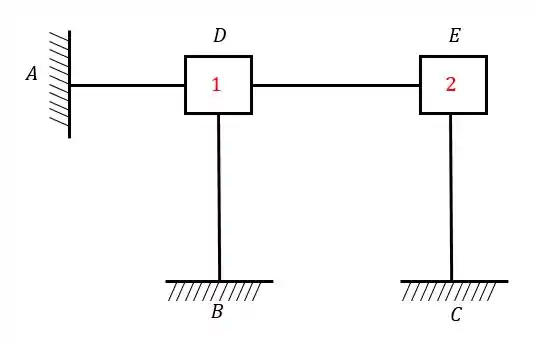
Passo 1
Vamos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são A e C. mas porque não o B? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros dois.
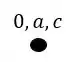
Lembre-se de sempre representar com letras minúsculas.
Passo 2
Agora a gente marca o deslocamento da nossa bolinha.
Passo 3
Agora vamos marcando os pontos subsequentes conforme os pontos que já temos. Se nós temos então podemos achar . Lembre sempre de utilizar retas perpendiculares às barras:
Passo 4
O ponto , que coincide com o ponto :
Essa é a nossa resposta final.
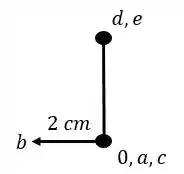
Resposta
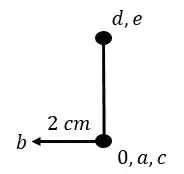
Exercício Resolvido #5
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio A recalca 3cm para baixo e 5 cm para esquerda.
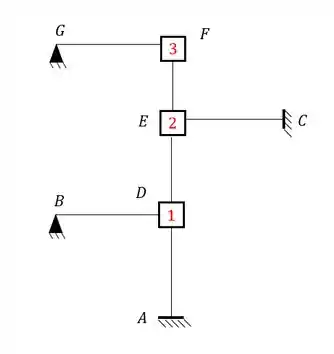
Passo 1
Vamos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são B, C e G. mas porque não o A? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros dois.
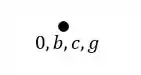
Lembre-se de sempre representar com letras minúsculas.
Passo 2
Em seguida devemos marcar a partir da origem o ponto que se deslocou, que no nosso caso foi o ponto A, que foi 3cm pra baixo e 5cm pra esquerda.
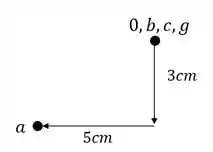
Passo 3
E agora o mais difícil que seria o ponto D.
Para determinar ele, precisamos usar a nossa regrinha básica. Escolhemos dois nós que nos auxiliem a achar o ponto D.
Podemos usar por exemplo os pontos B e A.
Devemos passar uma reta perpendicular a essas barras, e transferir elas pro nosso williot, sendo assim teremos que:
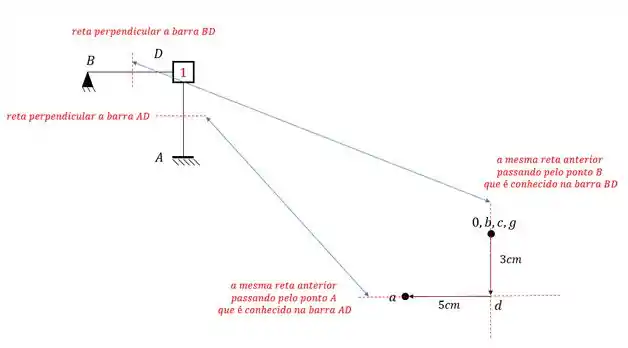
O ponto de encontro das retas é exatamente o nosso ponto D.
Passo 4
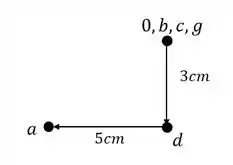
Para determinar o ponto E devemos usar os pontos C e D, sendo assim teremos que:
E vemos que nesse caso o ponto E coincide com o ponto D.
Passo 5
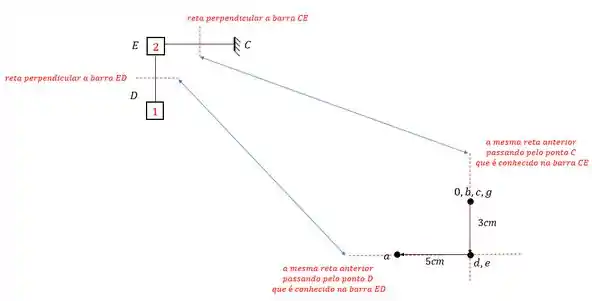
Para determinar o ponto F devemos usar os pontos E e G, sendo assim teremos que:
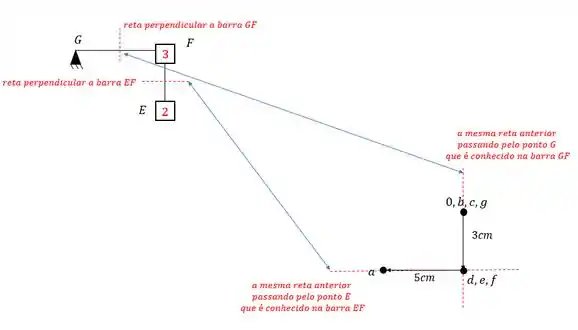
E vemos que nesse caso o ponto F coincide com o ponto D e E.
Assim nosso williot será.
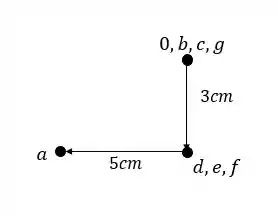
Resposta
Exercício Resolvido #6
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio sofre um recalque de para a esquerda e para baixo.
Passo 1
Fala aí, pessoal! Vamos começar marcando o nosso pontinho que sofre o deslocamento. Para isso vamos lembrar que o único ponto deslocável é aquele que sofre recalque, ou seja o .
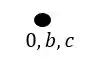
Aplicando o recalque de para à esquerda e para baixo vamos ter:
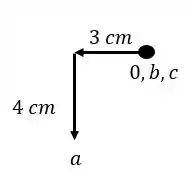
Aí a gente vai traçar as barras perpendiculares e ir calculando o pontos subsequentes.
Passo 2
Então vamos achar o williot de :
Olha como o nosso ponto fica exatamente abaixo de !
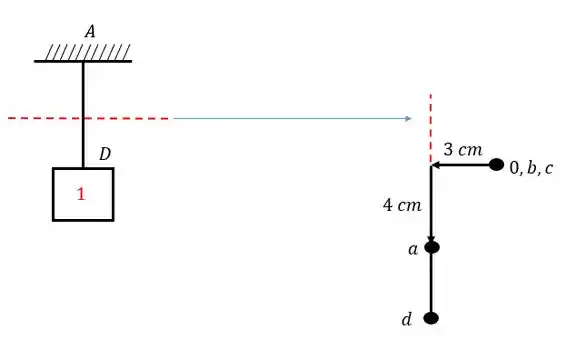
Passo 3
Agora a partir desse ponto vamos achar para o ponto . Lembrando que sempre vamos marcar o ponto baseado nas retas perpendiculares:
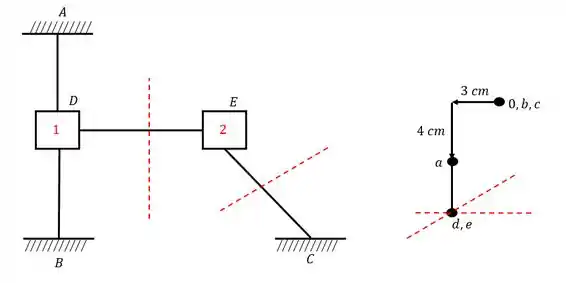
E pronto! Achamos todos os pontos!
Resposta
Exercício Resolvido #7
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio C recalca 2cm para baixo e 1,5 cm para direita.
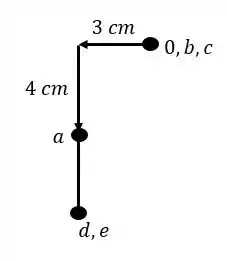
Passo 1
Vamos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são A e B. mas porque não o C? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros três.
![]()
Lembre-se de sempre representar com letras minúsculas.
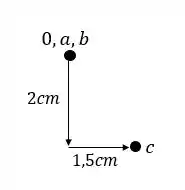
Passo 2
Em seguida devemos marcar a partir da origem o ponto que se deslocou, que no nosso caso foi o ponto C, que foi 2cm pra baixo e 1,5cm pra direita.
Passo 3
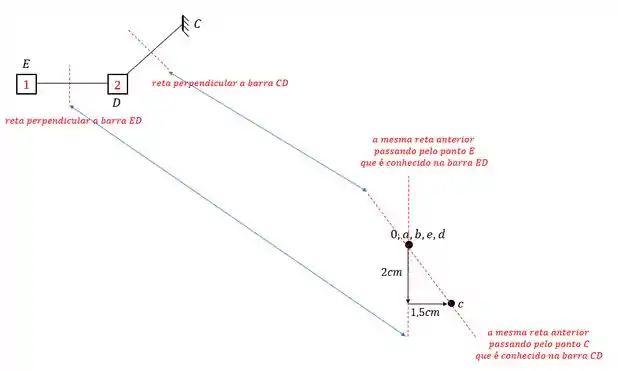
E agora o mais difícil que seria o ponto E.
Para determinar ele, precisamos usar a nossa regrinha básica. Escolhemos dois nós que nos auxiliem a achar o ponto E.
Podemos usar por exemplo os pontos B e A.
Devemos passar uma reta perpendicular a essas barras, e transferir elas pro nosso williot, sendo assim teremos que:
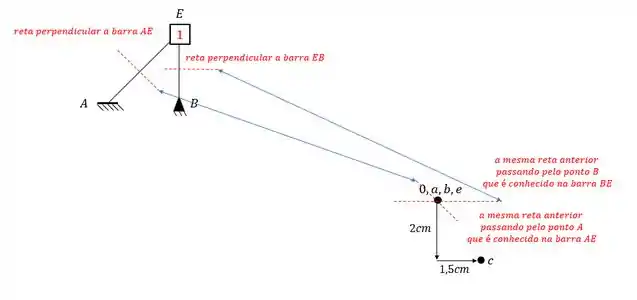
O ponto de encontro das retas é exatamente o nosso ponto E.
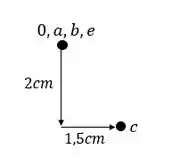
Passo 4
Para determinar o ponto D podemos usar os pontos E e C, sendo assim teremos que:
E vemos que nesse caso o ponto D coincide com o ponto A, B e E.
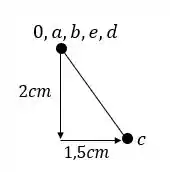
Assim nosso williot será.
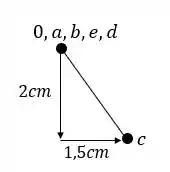
Resposta
Exercício Resolvido #8
Origem do Exercício
Determine o Williot da estrutura abaixo, sabendo que o apoio A recalca 1cm para baixo e 1 cm para esquerda.
Passo 1
Perceba que a nossa estrutura já contabiliza os números de deslocabilidades existentes, sendo assim, podemos partir direto para o nosso problema.
Agora já podemos começar o nosso passo a passo para o Williot. Sabemos que o primeiro passo é determinar o nosso zero, ou seja, a nossa origem. Junto com essa origem também podemos colocar os pontos que são indeslocaveis.
Com isso sabemos que os pontos indeslocaveis são B, C e F. mas porque não o A? exatamente porque ele deixa de ser indeslocavel quando sofre recalque, por isso podemos contabilizar apenas os outros dois.
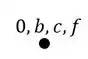
Passo 2
Em seguida devemos marcar a partir da origem o ponto que se deslocou, que no nosso caso foi o ponto A, que foi 1cm pra baixo e 1cm pra esquerda.
Passo 3
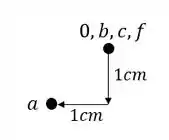
Como precisamos determinar um ponto que esteja ligado a dois que já foram determinados, iremos determinar o ponto D, que está ligado aos pontos B e A que já foram determinados no nosso williot. Sabemos que para isso precisamos passar uma reta perpendicular em cada barra, e fazer essa reta passar pelo ponto que for conhecido no williot e que faça parte da barra, sendo assim teremos que:
O ponto de encontro das retas é exatamente o nosso ponto D.
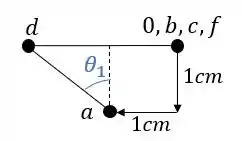
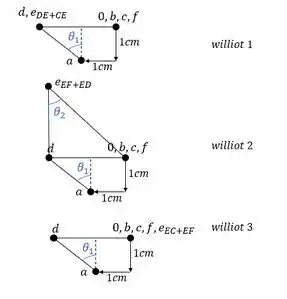
o ponto seguinte a ser determinado é o ponto E, porém perceba que ele pode ser determinado por diferentes combinações de barras, sendo assim devemos determinar diferentes posições de E, referentes as combinações especificas que cada uma das barras nós poderá dar, sendo assim teremos que:
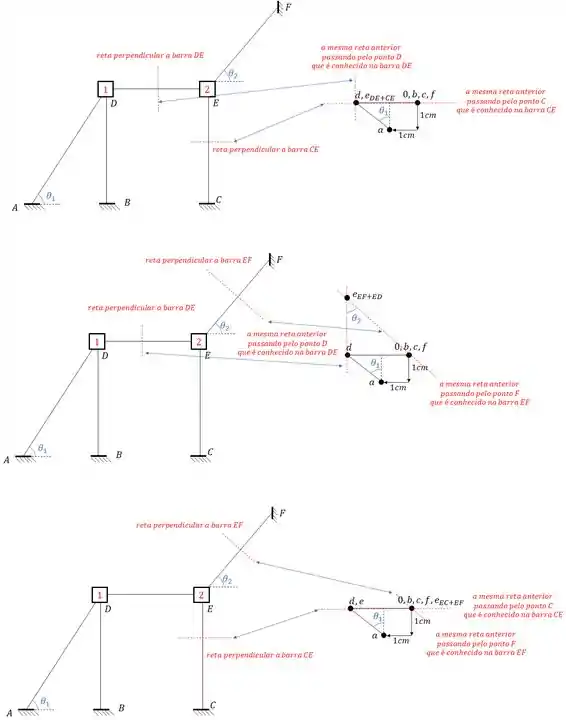
Perceba que então temos 3 Williot, certo? E qual dos 3 estará certo? Na verdade os 3 estão certos, mas cada um terá uma função diferente para determinação do deslocamento das barras.
O deslocamento sempre deve ser perpendicular a barra que estamos analisando, por exemplo, vamos supor que estivéssemos buscando saber qual a deformação da barra FE. Qual Williot seria o correto? Vamos testar cada caso e ver qual deles dará uma deformação perpendicular a barra.
- Williot 1 (combinação das barras DE e EC)
- Williot 2 (combinação das barras DE e FE)
- Williot 3 (combinação das barras CE e FE)
Como sabemos a regrinha do deslocamento é sempre do ponto que determinamos primeiro para o ponto que determinamos em segundo, ou seja, no williot se dará do nó F para o nó E, sendo assim teremos que:
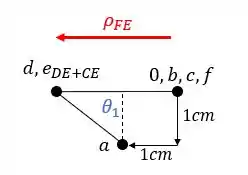
Perceba que esse deslocamento não é perpendicular a barra FE, logo, esse não é o williot que devemos usar para essa barra.
Como sabemos a regrinha do deslocamento é sempre do ponto que determinamos primeiro para o ponto que determinamos em segundo, ou seja, no williot se dará do nó F para o nó E, sendo assim teremos que:
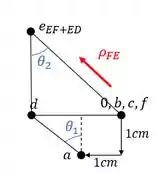
Perceba que esse deslocamento é perpendicular a barra FE, logo, esse é o williot que devemos usar para essa barra.
Como sabemos a regrinha do deslocamento é sempre do ponto que determinamos primeiro para o ponto que determinamos em segundo, ou seja, no williot se dará do nó F para o nó E, sendo assim teremos que:
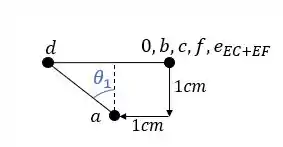
Perceba que nesse caso o williot dará para a barra EF um deslocamento de zero, que para a barra será indiferente já que já descobrimos a deformação dela no caso anterior, se por acaso a deformação nesse terceiro williot também desse perpendicular a barra, usaríamos ele somando ou subtraindo a deformação que já achamos no caso anterior.
Isso então significa que o segundo williot é o correto? Não, todos os 3 williot’s estão corretos, no caso acima, ESPECIFICAMENTE para a barra EF SOMENTE o segundo williot vale.
Porém se a barra analisada fosse a barra CE, o único williot que teria uma deformação perpendicular a essa barra seria o Williot 1.
E por fim para a barra DE o único williot com deformação perpendicular a barra seria a o williot 2.
Ou seja, teríamos que usar os 3 Williot’s para as nossas barras, e não só 1. Sendo assim a resposta final para determinação do Williot da nossa estrutura será:
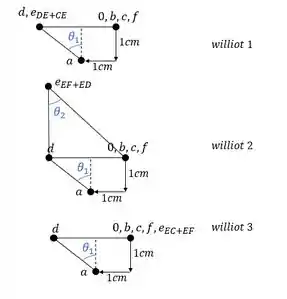
Resposta