Apoios Elásticos em estruturas com deslocabilidade externa
Produzido por Pablo RicardoTeoria
Introdução
Já aprendemos como resolver um exemplo de apoio elástico em estruturas com desocabilidade interna, e vimos que a estrutura que deveríamos usar era uma chapa no lugar da mola do tipo engaste elástico.
No caso de molas verticais e horizontais, ao invés de pormos chapas, iremos por o nosso velo amigo apoio do primeiro gênero, e será esse apoio que ira nos ajudar, sendo assim vamos ver um exemplo e um passo a passo pra resolver esse exemplo.
Exemplo
Imagine que a barra abaixo tenha e que a rigidez da mola seja de Sabendo disso determine o deslocamento vertical na mola.
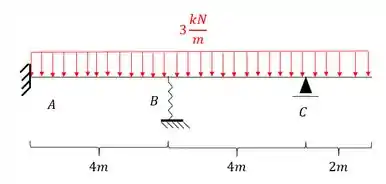
E agora vamos usar tudo que aprendemos até aqui, para compor o nosso passo a passo.
Passo 1 – simplificação da estrutura
Perceba que já vimos isso antes, a nossa estrutura possui um balanço, e podemos sumir com ele usando um momento concentrado em C que represente ele, ou seja, se a carga que vemos traciona as fibras da parte de cima, podemos simplificar ele com um momento que signifique o mesmo. Dessa maneira teremos que:
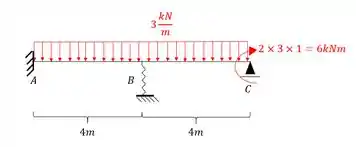
Passo 2 – Travamentos das deslocabilidades
Até aqui já vimos muitas e muitas vezes como determinar as nossas deslocabilidades. Por isso podemos passar bem rápido por isso. A única coisa de diferente é que vamos substituir a nossa mola por uma poio do primeiro gênero, fizemos a mesma coisa na aula que falava de apoios elásticos em estruturas com deslocabilidade interna, e lá trocávamos a mola por uma chapa, aqui é o mesmo princípio. O que é importante é que sempre devemos lembrar que esse apoio é uma mola, isso vai ser importante para os cálculos. Sendo assim nosso travamento será.
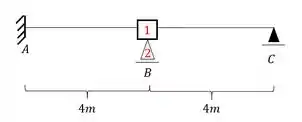
Passo 3 – Cálculo dos efeitos no sistema 0 (
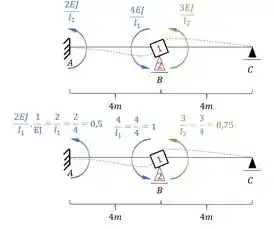
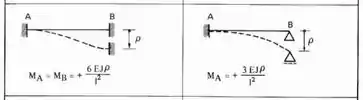
Sabemos que para determinar esses caras precisamos usar a nossa tabela de momentos recíprocos e analisar o nosso carregamento, fazendo isso a fórmula que devemos usar é:
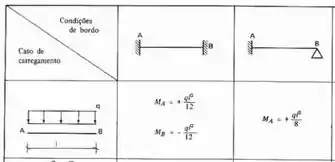
Usando isso na nossa estrutura, e lembrando que todo momento aplicado na estrutura transfere metade do momento dele para outra extremidade mantendo o sinal, teremos que:
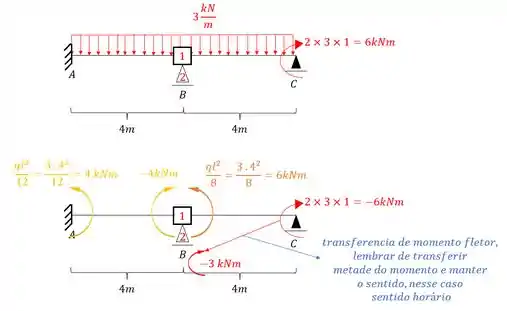
Assim fica fácil determinar o que seria os momentos que agem na chapa 1, sendo assim teremos que:
E para determinar precisamos definir as reações de apoio, sendo assim teremos que:
Como já sabemos que a reação de apoio mantém o mesmo sentido do calculado, e que ainda consideramos de baixo pra cima positivo, teremos que:
Passo 4 – Cálculo dos efeitos no sistema 1 (
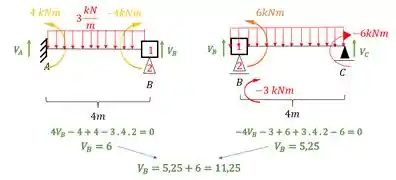
Esse aqui já estamos até cansado de ver, basta rotacionarmos a chapa e determinarmos os momentos que aparecem nela e a reação que aparece no apoio. Como temos de um lado um engaste e do outro um apoio, e no meio uma chapa, usaremos pra uma metade uma fórmula e para outra a outra fórmula, que sigam os critérios determinados, sendo assim teremos que:
Lembrando que usamos como fator redutor, teremos que:
E para o outro sabemos que devemos determinar a reação de apoio, sendo assim teremos que:
Passo 5 – Cálculo dos efeitos no sistema 2 (
É aqui que entra o nosso diferencial, sabemos que temos que mover o apoio em 2 em uma unidade, mas lembre-se que ele representa uma mola, ou seja, sabemos que a fórmula para determinar a deformação em uma mola é dada por:
No nosso caso podemos determinar a força na mola porque ela irá se deformar a 1 unidade que iremos aplicar, sendo assim teremos que:
Mas ainda temos as forças devido aos momentos da deformação, e essas encontraremos usando as seguintes fórmulas:
Lembrando que usamos como fator redutor, teremos que:
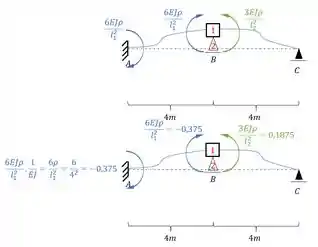
E para o outro sabemos que devemos determinar a reação de apoio, sendo assim teremos que:
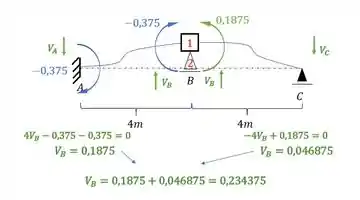
Porém, não podemos esquecer de somar o valor referente ao deslocamento na mola, tomando o seguinte cuidado, pois, se dividimos tudo por EJ, também devemos fazer o mesmo com a carga na mola.
E por fim, devemos analisar o sinal, E ISSO É MUITO IMPORTANTE. Pois iremos arbitrar que o sentido da reação de apoio da mola é no mesmo sentido da deformação imposta, ou seja, se deformamos a estrutura pra cima, a mola terá uma reação pra cima, se deformacemos a mola pra baixo, ela nos daria uma reação pra baixo, sendo assim teremos que:
Isso é muito importante pois estamos arbitrando esse sinal para facilitar, ou seja, sempre iremos considerar a força da mola no sentido da deformação imposta.
Passo 6 – solução do sistema
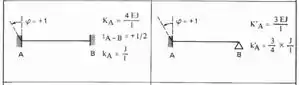
Agora vem a parte mais simples, que e resolver o sisteminha, sendo assim teremos que:
Substituindo:
Assim teremos que:
Lembre-se que o objetivo era a deformação na mola, certo? Ou seja, precisamos de , mas precisamos multiplicar ele pelo nosso fator de rigidez:
Como deu negativo, significa que o sentido que arbitramos de deformação é invertido, ou seja, ao invés de deformar pra cima, a mola deforma pra baixo.
Ufa, enfim terminamos, agora bora fazer exercício pra ficar craque !!!!

Passo 2 – Travamentos das deslocabilidades
Passo 3 – Cálculo dos efeitos no sistema 0 ( β 10 e β 2 0 )
Passo 4 – Cálculo dos efeitos no sistema 1 ( β 1 1 e β 2 1 )
Passo 5 – Cálculo dos efeitos no sistema 2 ( β 22 e β 12 )
Passo 6 – solução do sistema
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Para a viga abaixo com uma mola vertical em B, determine a deformação vertical na mola.
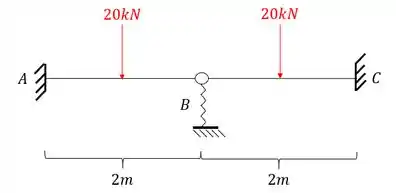
Passo 1
Pela nossa teoria temos que lembrar que o travamento da estrutura é feito levando em conta as deslocabilidades.
- Deslocabilidade Interna
- Temos um engaste em A e C logo nesses pontos não precisamos por chapas de travamento da nossa estrutura.
- No ponto B temos uma rótula, e sabemos que todo nó com rótula não precisa de chapa também.
- Com isso não temos deslocabilidades internas
- Deslocabilidade Externa
- Os pontos A e C são engastes, logo, também não tem deslocabilidade externa
- O ponto B é uma mola, logo, consideramos ela como um ponto propício a se deslocar, e com isso precisamos travar ele.
- E pra fazermos isso precisamos trocar a nossa mola por um apoio do primeiro gênero (lembrando ainda que se trata de uma mola e por isso teremos que fazer um acréscimo em algum momento)
Com isso teremos que:
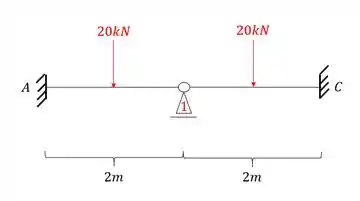
Passo 2
Determinando a deslocabilidade e o que ela é precisamos determinar o que é , e sabemos que como se trata de um apoio do primeiro gênero, iremos precisar da reação de apoio.
Para definirmos a reação de apoio precisamos do passo a passo completo.
- Primeiro determinamos a fórmula
- Segundo definimos os momentos na nossa estrutura
- Determinando as reações de apoio
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E isso é bem simples, a barra AB possui um engaste em A e um apoio em B, logo, engaste e apoio. E para a barra BC acontece a mesma coisa. E como em ambas temos uma carga concentrada no meio das vigas, a nossa fórmula será.
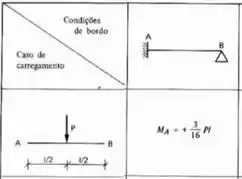
Aplicando na nossa estrutura teremos que:
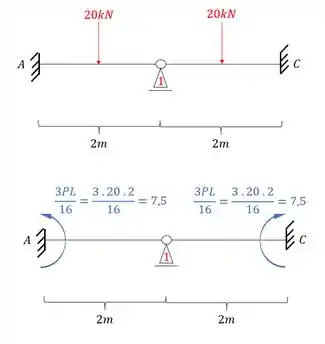
Lembre-se que como temos um apoio do primeiro gênero, precisamos determinar a reação de apoio, dessa maneira teremos que:
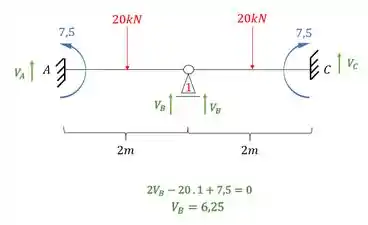
Perceba que a reação deu de baixo pra cima, que é o nosso sentido positivo. E também podemos ver que temos 2 reações de apoio na mesma direção, sendo assim teremos que:
Passo 3
Agora só precisamos do valor de . Como se trata de um apoio do primeiro gênero só precisamos deslocar ele de uma unidade no sentido que definimos como positivo.
Lembre-se que quando usamos deslocamentos impostos usamos a seguinte fórmula:
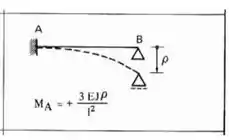
Deslocando a nossa viga teremos que:
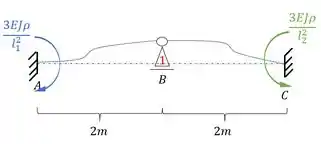
Podemos também dividir tudo por EJ, e lembrar que estamos usando , assim a nossa estrutura passa a ser:
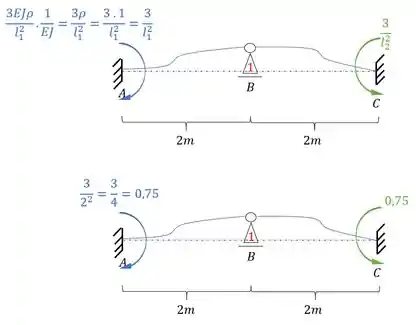
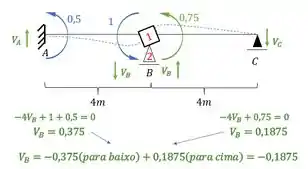
Como o nosso objetivo são as reações de apoio, vamos determinar elas:
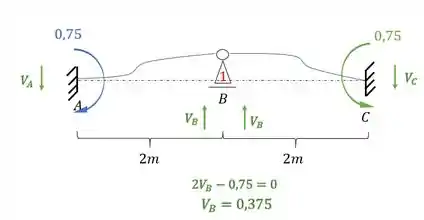
Como temos duas reações de apoio, pra cima, que é o sentido positivo, podemos determinar muito facilmente o valor de , sendo assim teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 3
Resolvendo o nosso sisteminha, teremos que:
Mas lembre-se que a gente dividiu todos os termos por EJ, ou seja, se quisermos definir a deformação final na mola, precisamos dividir o nosso por EJ
Resposta
Exercício Resolvido #2
Origem do Exercício
Para a viga abaixo com uma mola vertical em B, determine a deformação vertical na mola.
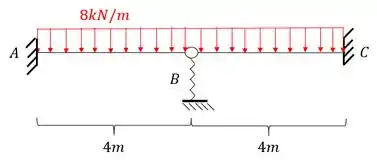
Passo 1
Pela nossa teoria temos que lembrar que o travamento da estrutura é feito levando em conta as deslocabilidades.
- Deslocabilidade Interna
- Temos um engaste em A e C logo nesses pontos não precisamos por chapas de travamento da nossa estrutura.
- No ponto B temos uma rótula, e sabemos que todo nó com rótula não precisa de chapa também.
- Com isso não temos deslocabilidades internas
- Deslocabilidade Externa
- Os pontos A e C são engastes, logo, também não tem deslocabilidade externa
- O ponto B é uma mola, logo, consideramos ela como um ponto propício a se deslocar, e com isso precisamos travar ele.
- E pra fazermos isso precisamos trocar a nossa mola por um apoio do primeiro gênero (lembrando ainda que se trata de uma mola e por isso teremos que fazer um acréscimo em algum momento)
Com isso teremos que:
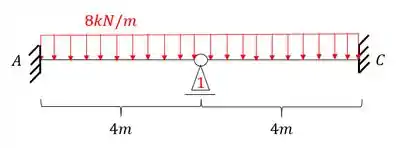
Passo 2
Determinando a deslocabilidade e o que ela é precisamos determinar o que é , e sabemos que como se trata de um apoio do primeiro gênero, iremos precisar da reação de apoio.
Para definirmos a reação de apoio precisamos do passo a passo completo.
- Primeiro determinamos a fórmula
- Segundo definimos os momentos na nossa estrutura
- Determinando as reações de apoio
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E isso é bem simples, a barra AB possui um engaste em A e um apoio em B, logo, engaste e apoio. E para a barra BC acontece a mesma coisa. E como em ambas temos uma carga distribuída por toda viga, a nossa fórmula será.
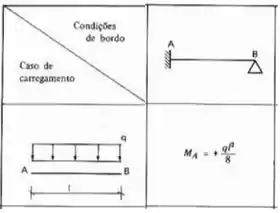
Aplicando na nossa estrutura teremos que:
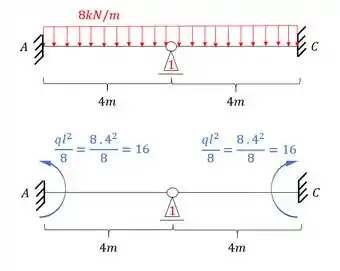
Lembre-se que como temos um apoio do primeiro gênero, precisamos determinar a reação de apoio, dessa maneira teremos que:
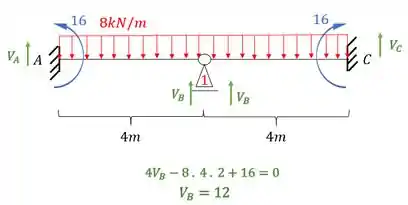
Perceba que a reação deu de baixo pra cima, que é o nosso sentido positivo. E também podemos ver que temos 2 reações de apoio na mesma direção, sendo assim teremos que:
Passo 3
Agora só precisamos do valor de . Como se trata de um apoio do primeiro gênero só precisamos deslocar ele de uma unidade no sentido que definimos como positivo.
Lembre-se que quando usamos deslocamentos impostos usamos a seguinte fórmula:
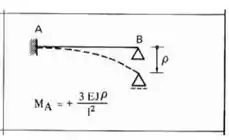
Deslocando a nossa viga teremos que:
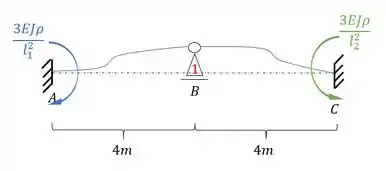
Podemos também dividir tudo por EJ, e lembrar que estamos usando , assim a nossa estrutura passa a ser:
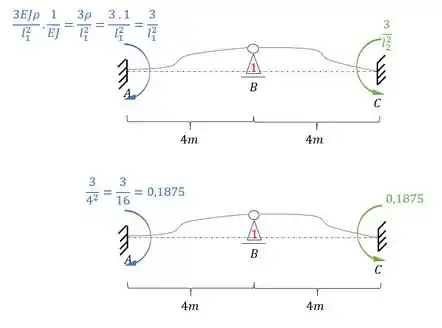
Como o nosso objetivo são as reações de apoio, vamos determinar elas:
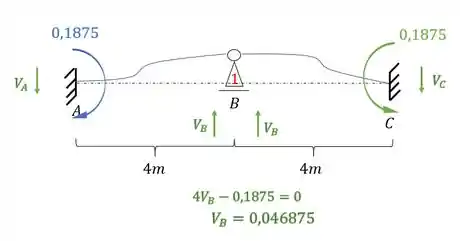
Como temos duas reações de apoio, pra cima, que é o sentido positivo, podemos determinar muito facilmente o valor de , sendo assim teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 3
Resolvendo o nosso sisteminha, teremos que:
Mas lembre-se que a gente dividiu todos os termos por EJ, ou seja, se quisermos definir a deformação final na mola, precisamos dividir o nosso por EJ
Resposta
Exercício Resolvido #3
Origem do Exercício
Para a viga abaixo com uma mola vertical em B, determine a deformação vertical na mola.
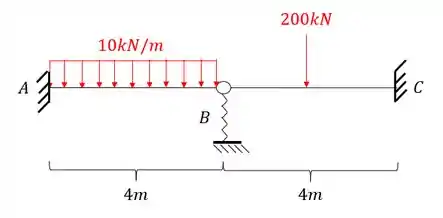
Passo 1
Pela nossa teoria temos que lembrar que o travamento da estrutura é feito levando em conta as deslocabilidades.
- Deslocabilidade Interna
- Temos um engaste em A e C logo nesses pontos não precisamos por chapas de travamento da nossa estrutura.
- No ponto B temos uma rótula, e sabemos que todo nó com rótula não precisa de chapa também.
- Com isso não temos deslocabilidades internas
- Deslocabilidade Externa
- Os pontos A e C são engastes, logo, também não tem deslocabilidade externa
- O ponto B é uma mola, logo, consideramos ela como um ponto propício a se deslocar, e com isso precisamos travar ele.
- E pra fazermos isso precisamos trocar a nossa mola por um apoio do primeiro gênero (lembrando ainda que se trata de uma mola e por isso teremos que fazer um acréscimo em algum momento)
Com isso teremos que:
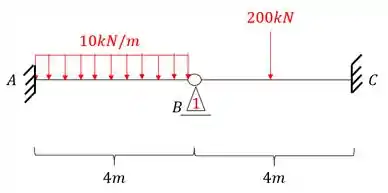
Passo 2
Determinando a deslocabilidade e o que ela é precisamos determinar o que é , e sabemos que como se trata de um apoio do primeiro gênero, iremos precisar da reação de apoio.
Para definirmos a reação de apoio precisamos do passo a passo completo.
- Primeiro determinamos a fórmula
- Segundo definimos os momentos na nossa estrutura
- Determinando as reações de apoio
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E isso é bem simples, a barra AB possui um engaste em A e um apoio em B, logo, engaste e apoio. E para a barra BC acontece a mesma coisa. E como em ambas temos uma carga distribuída por toda viga, a nossa fórmula será.
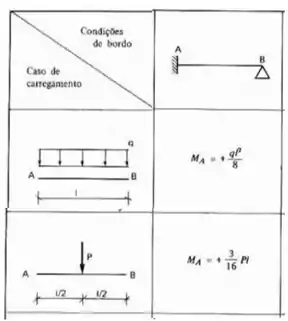
Aplicando na nossa estrutura teremos que:
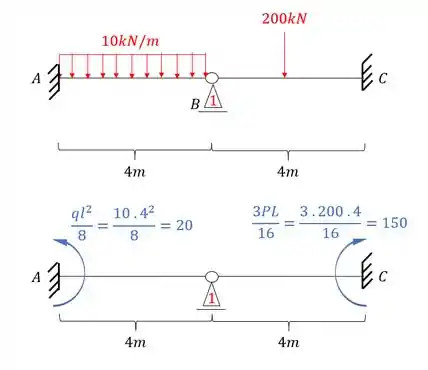
Lembre-se que como temos um apoio do primeiro gênero, precisamos determinar a reação de apoio, dessa maneira teremos que:
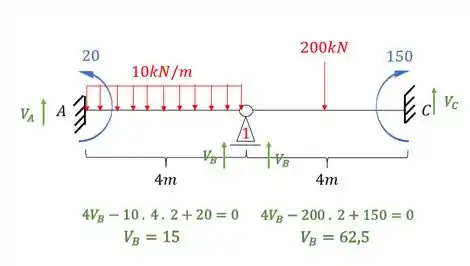
Perceba que a reação deu de baixo pra cima, que é o nosso sentido positivo. E também podemos ver que temos 2 reações de apoio na mesma direção, sendo assim teremos que:
Passo 3
Agora só precisamos do valor de . Como se trata de um apoio do primeiro gênero só precisamos deslocar ele de uma unidade no sentido que definimos como positivo.
Lembre-se que quando usamos deslocamentos impostos usamos a seguinte fórmula:
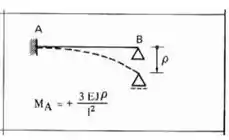
Deslocando a nossa viga teremos que:
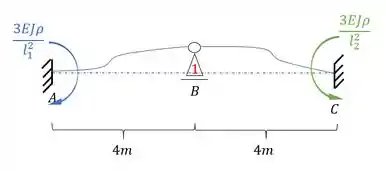
Podemos também dividir tudo por EJ, e lembrar que estamos usando , assim a nossa estrutura passa a ser:
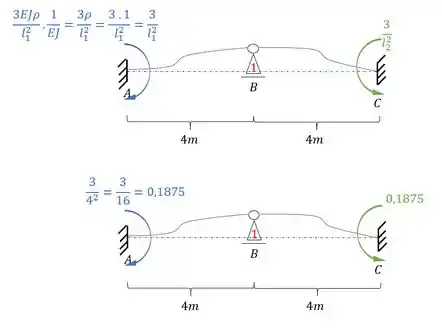
Como o nosso objetivo são as reações de apoio, vamos determinar elas:
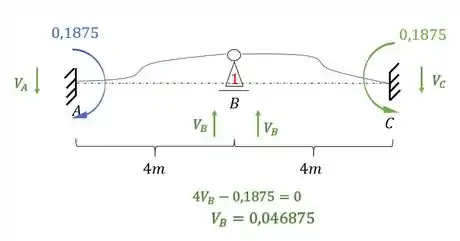
Como temos duas reações de apoio, pra cima, que é o sentido positivo, podemos determinar muito facilmente o valor de , sendo assim teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 3
Resolvendo o nosso sisteminha, teremos que:
Mas lembre-se que a gente dividiu todos os termos por EJ, ou seja, se quisermos definir a deformação final na mola, precisamos dividir o nosso por EJ
Resposta
Exercício Resolvido #4
Origem do Exercício
Para a estrutura abaixo, determine o deslocamento horizontal do ponto B do pórtico dado.
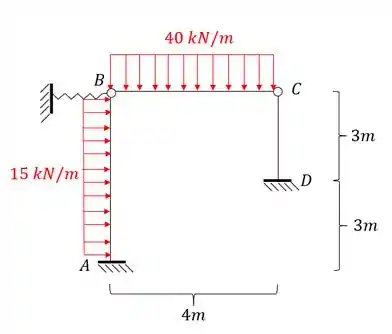
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso, com mola, precisamos trocar a nossa mola por uma poio do primeiro gênero , dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
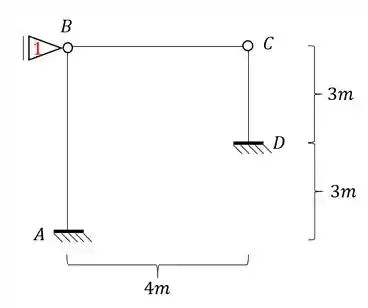
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de . Mas perceba que a carga de que age na vertical, não irá produzir reações de apoio na horizontal, então não precisamos nos preocupar com ela.
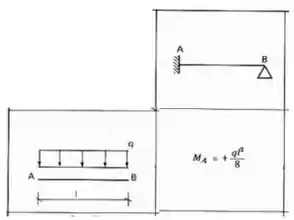
Em contra partida a carga distribuída de , irá produzir um momento no nosso apoio em A, e perceba que essa barra é engastada em A mas rotulada em B, ou seja, é do tipo engastada e rotulada, e sendo assim, a nossa equação será:
Aplicando ela na nossa estrutura teremos que:
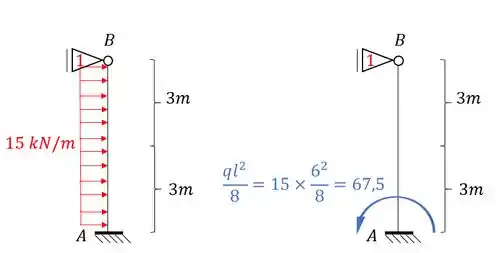
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
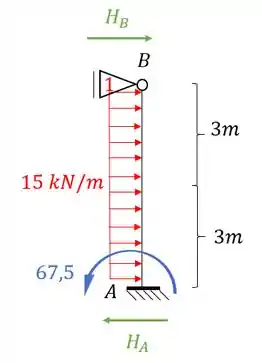
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo, mas se você fizer o passo completo vai ver que faz sentido. Porque imagine se invertermos as reações, teríamos o seguinte:
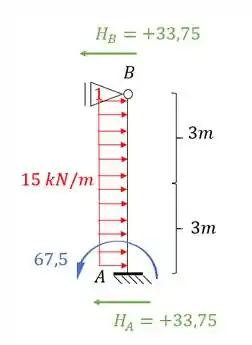
Perceba que se invertermos os vetores, o sinal volta a ser positivo, porém veja que o sentido é para trás, e como vimos na teoria, para determinação de rigidez, consideramos pra frente positivo e pra trás negativo, com isso, o nosso valor de será:
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
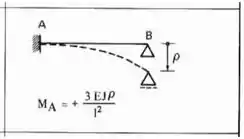
Fazendo esse deslocamento na nossa estrutura teremos que:
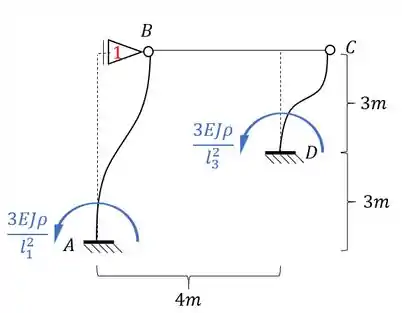
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
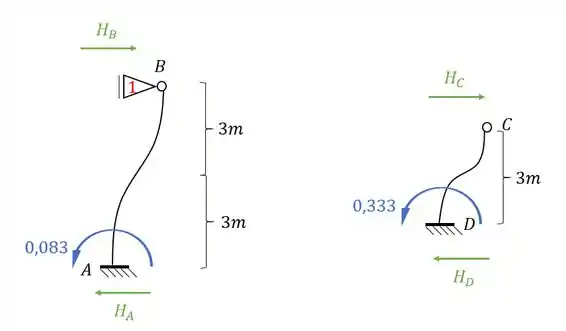
Perceba que precisamos dos valores de e . Com isso teremos que:
Para teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #5
Origem do Exercício
Para a estrutura abaixo, determine o deslocamento horizontal do ponto B do pórtico dado.
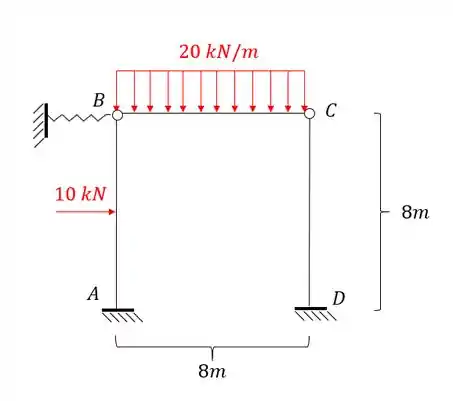
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso, por se tratar de uma mola precisamos travar esse movimento , especificamente, devemos por no lugar da mola um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
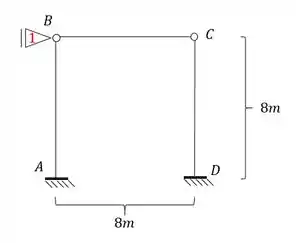
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de . Mas perceba que a carga de que age na vertical, não irá produzir reações de apoio na horizontal, então não precisamos nos preocupar com ela.
Em contra partida a carga concentrada de 10kN, irá produzir um momento no nosso apoio em A, e perceba que essa barra é engastada em A mas rotulada em B, ou seja, é do tipo engastada e rotulada, e sendo assim, a nossa equação será:
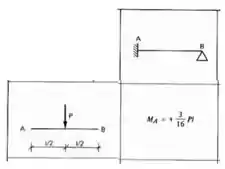
Aplicando ela na nossa estrutura teremos que:
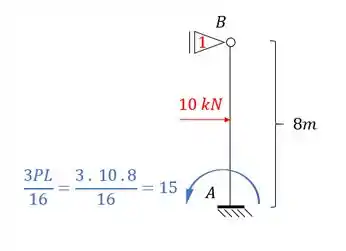
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
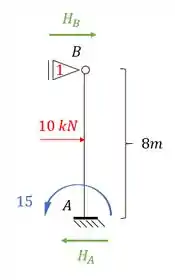
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo, mas se você fizer o passo completo vai ver que faz sentido. Porque imagine se invertermos as reações, teríamos o seguinte:
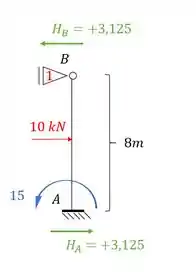
Perceba que se invertermos os vetores, o sinal volta a ser positivo, porém veja que o sentido é para trás, e como vimos na teoria, para determinação de rigidez, consideramos pra frente positivo e pra trás negativo, com isso, o nosso valor de será:
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
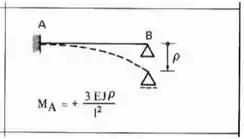
Fazendo esse deslocamento na nossa estrutura teremos que:
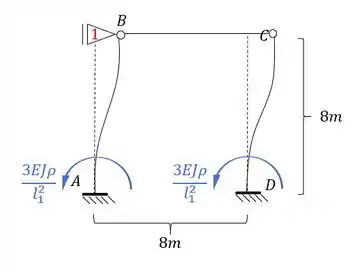
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
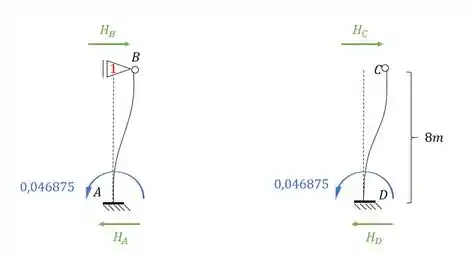
Perceba que precisamos dos valores de e . Com isso teremos que:
Mas lembre-se que . Sendo assim teremos que:
MAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAS, não se esqueça que temos uma mola, que também segue algumas regrinhas que temos que ficar bem atentos na hora de resolver elas.
- Primeiro sabemos que a força na mola fica no mesmo sentido da deformação, ou seja, pra cima.
- Também sabemos que o valor dessa força segue a seguinte fórmula:
E esses dois valores nos temos, pois sabemos que:
Mas uma coisa muito importante que devemos lembrar é que dividimos todos os termos da nossa estrutura por EJ, ou seja, a nossa amiga mola não pode fugir a essa regra.
Dessa maneira teremos que:
Essa contribuição devemos somar ao nosso fator
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que: