Deslocabilidade externa – Recalque de apoio
Produzido por Pablo RicardoTeoria
Introdução
Nessa aula basicamente vamos misturar os conceitos de duas outras aulas.
- Primeiro a aula sobre williot para recalques de apoio.
- E em segundo lugar a nossa aula sobre solução de estruturas com deslocabilidade externa.
Pra ficar mais fácil vamos usar um exemplo, o mesmo que usamos na aula passada, e com isso vamos entender como funciona a solução dos problemas em estruturas com deslocabilidade externa e recalque do apoio.
Exemplo
Imagine que a estrutura abaixo sobre um recalque no apoio D, de tal maneira que o apoio D desce 1cm na vertical e vai para direita 1 cm também, sabendo disso, quais seriam a rotação do ponto B e o seu deslocamento horizontal? Usando .
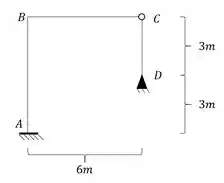
Passo 1 – determinação das deslocabilidades
Sabemos que temos que determinar as deslocabilidades da nossa estrutura, então não vamos nos aprofundar muito nisso nessa aula já que vimos bastante disso nas aulas anteriores. Sendo assim, a nossa estrutura travada nas deslocabilidades que tem, ficará da seguinte maneira:
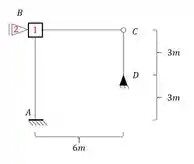
Passo 2 – determinar o valor de e
Nesse caso o nosso carregamento é um recalque de apoio, certo? Ou seja, vimos que para o método dos deslocamentos o que devemos usar quando houver um recalque de apoio é desenhar o nosso williot, que também como vimos nas aulas anteriores não vamos nós aprofundar e aqui vamos ir direto ao ponto, sendo assim teremos que:
- Determinação da origem
- Ponto que se deslocou
- Ponto B e C
A origem é determinada pelo ponto que não irá se deslocar, que no nosso caso será apenas o apoio A.
![]()
Em seguida determinamos o ponto que se deslocou (que no nosso caso foi o ponto D) com base no ponto que é a origem, e seguindo os recalques pré estabelecidos, sendo assim teremos que:
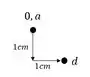
O ponto seguinte a se determinado é o ponto B, e para isso traçamos uma perpendicular as retas que compõem ele e levamos até os pontos dessa reta que são conhecidos, assim teremos que:

Perceba que os pontos B e C que são importantes pra gente, estão na reta que desconhecemos, porém, podemos deduzir o que acontece com o ponto C, e assim determinar o ponto B.
Sabemos que o ponto C é uma rótula, certo? E rótulas permitem rotações, certo?
Se o nosso ponto D descer 1cm, o nosso ponto C também irá descer, porém se o ponto D for 1 cm pra frente, a rótula em C irá rodar, e se a rótula em C rodar, ela não irá deslocar. E assim sabemos então que o ponto C desceu 1 cm, e no nosso williot será.
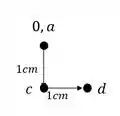
Conhecendo o ponto C, determinamos facilmente B levando a reta dele pro williot,
assim teremos que:

Tendo os pontos do williot, nós devemos determinar os deslocamentos e as rigidezes ligadas a esses deslocamentos, sendo assim teremos que:
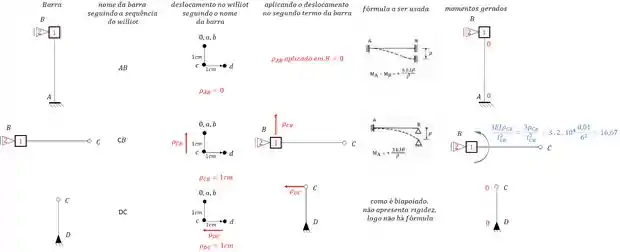
Podemos perceber que com relação ao momento que age na chapa 1, sabemos que ele produzira , que será dado por:
E para teriamos que calcular a reação de apoio, certo? Mas veja que apenas a parra BC possui momentos fletores, e esse momento fletor só pode produzir reações verticais, como vemos aqui embaixo:
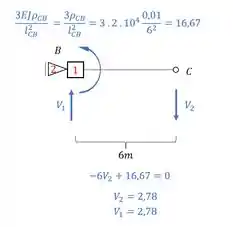
Passo 3 – determinar o valor de e
Perceba que agora começamos em um conceito que já conhecemos, como o segundo termo é 1, significa que temos que rotacionar a chapa 1, com isso teremos que dividindo esse termo por EJ, teremos que:
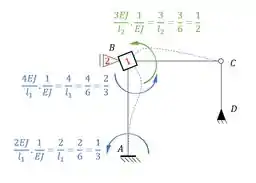
E lembre-se que sempre que rotacionamos uma chapa, usamos a seguinte equação:
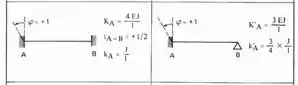
Dessa maneira teremos que:
Mas como determinamos o que acontece com ? Basta entender o que ele significa. Ele é o que acontece no apoio 2 devido a rotação na chapa 1, ou seja, precisamos das reações de apoio, fazendo o que já aprendemos, podemos fazer o seguinte:
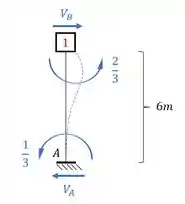
Fazendo o somatório de momentos em B teremos que:
Como o sinal se conserva pra reação de apoio, e precisamos do que está agindo na direção do apoio do primeiro gênero, usaremos o valor de no mesmo sentido que calculamos, ou seja, podemos dizer que:
Passo 4 – Determinar o valor de e
Agora que entra o nosso novo conceito, no passo anterior nós rotacionamos a nossa chapa em 2 grau certo? Mas agora não temos mais uma chapa, e sim um apoio, e nesse caso também iremos impor uma deformação, mas não mais de rotação, mas de deslocamento. Como decidimos que da esquerda para direita é positivo, iremos deslocar o nosso apoio do primeiro gênero da esquerda para direita e em uma unidade.
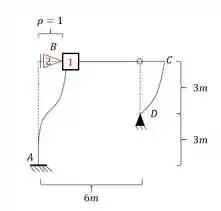
E sempre que deslocarmos um apoio devemos prestar aa tenção em duas coisas.
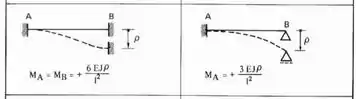
- A fórmula a ser usada é essa aqui em baixo:
- E a segunda coisa a ser notada é que esse deslocamento geralmente afeta mais de uma barra, por exemplo, perceba que a nossa barra AB foi dobrada, mas a nossa barra CD também foi dobrada. No nosso exemplo a barra CD por ser Bi-rotulada não apresentará momentos, mas só por isso que não iremos considerar momentos nela, se fosse outra barra com algum tipo de engaste, deveríamos considerar momentos em ambas as barras. Em vários exercícios iremos ver melhor isso, mas é importante já irmos com esse pensamento.
- Rotação do ponto B
- Deslocamento do ponto B
Dessa maneira teremos que:
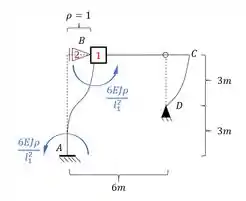
Mas lembre-se que impomos uma deformação de , e devemos lembrar também que dividimos no outro caso tudo por EJ, então obrigatoriamente teremos que dividir por EJ também aqui, assim teremos:
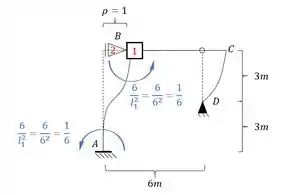
Assim teremos que a rigidez que age no ponto 1 devido o movimento do apoio 2 será dado por:
E o que acontece no apoio 2 devido o movimento do apoio 2? É ai que determinamos as reações de apoio:
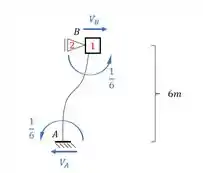
Como o sinal se conserva pra reação de apoio, e precisamos do que está agindo na direção do apoio do primeiro gênero, usaremos o valor de no mesmo sentido que calculamos, ou seja, podemos dizer que:
Passo 5 – Determinar as deformações
Agora é simples, todo o resto continua igual, o que acrescentamos aqui foi simplesmente como resolver um problema com deslocabilidade externa, e fazemos como sempre fazemos com a chapa, só que ao invés de rotacionarmos em um grau, deslocamos em uma unidade na horizontal, sendo assim teremos que apenas resolver o sistema gerado que será:
Resolvendo esse sistema teremos que:
E se pararmos para prestar a atenção vamos ver que representa a rotação do ponto B e o deslocamento horizontal do ponto B, que é exatamente o que a gente precisa. Mas devemos lembrar que simplificamos a nossa equação dividindo tudo por EJ, sendo assim, precisamos fazer isso aqui para termos os deslocamentos reais, e assim teremos que:
Se deu negativo é porque se rotacionamos a chapa no sentido anti-horário, significa que na realidade ela rotaciona no sentido horário.
Como deu positivo, significa que escolhemos o sentido certo, ou seja, da esquerda para direita.
Ou seja, com isso tudo, conseguimos entender como resolver problemas com deslocabilidade externa, e como determinar as suas deformações. E os momentos são determinados da mesma maneira que antes, podemos fazer da seguinte maneira:
Que substituindo teremos que:
E perceba que usamos os valores determinados no sistema, e não os valores das deformações reais, e com isso conseguimos resolver qualquer sistema com deslocabilidades externas, beleza? Bora fazer alguns exercícios para podermos ficar craques nessa área.
Passo 2 – determinar o valor de β 10 e β 20
Passo 3 – determinar o valor de β 11 e β 21
Passo 4 – Determinar o valor de β 22 e β 12
Passo 5 – Determinar as deformações
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Determine o williot da estrutura abaixo sabendo que o apoio em A desceu 2 cm e andou 5 cm para esquerda.
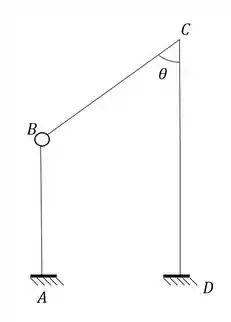
Passo 1
Devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o engaste em D, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
A partir desse ponto podemos marcar facilmente o ponto A, que desce 2 e anda 5 cm para esquerda, sendo assim o ponto A passa a ser.
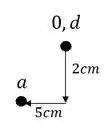
Como nem o ponto B e nem o ponto C estão ligados a dois pontos conhecidos, podemos achar um deles por suposição, e depois encontrar o outro.
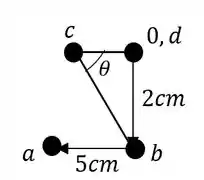
O ponto B por exemplo, sabemos que ele desce 2 cm junto com o ponto A, porém apenas o ponto A segue 5cm para frente, já que a rótula em B fará a barra rotacionar e não deslocar em 5 cm. Dessa maneira podemos descobrir facilmente B no nosso williot descendo ele 2cm a partir do ponto indeslocavel, ou da origem, sendo assim teremos que:
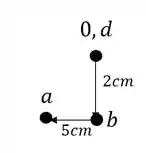
Agora a partir de B e de D podemos determinar o ponto C, basta traçarmos perpendiculares a cada uma das barras que se ligam a C, e a partir delas determinar o ponto de encontro no williot.
Fazendo isso teremos que:
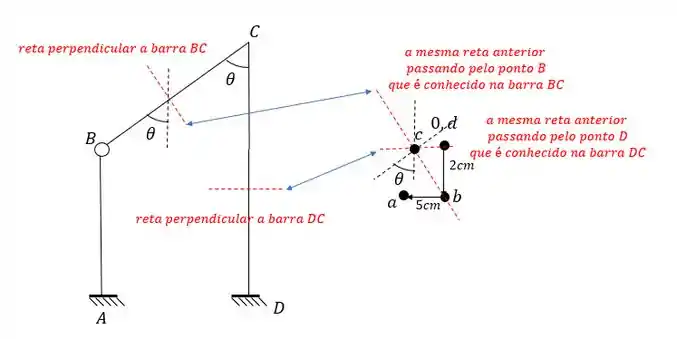
E assim determinamos o nosso wiliot completo que será dado por:
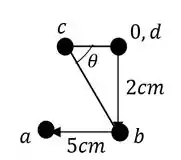
Resposta
Exercício Resolvido #2
Origem do Exercício
A estrutura abaixo sofreu um recalque no apoio A de 2cm para baixo e 1 cm para esquerda. Sabendo disso determine o deslocamento horizontal do ponto B. use
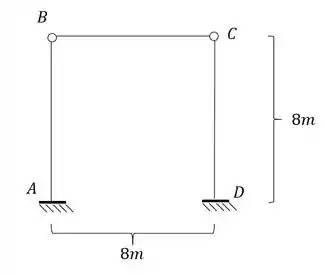
Passo 1
Para podermos determinarmos a deformação precisamos antes de tudo determinar o williot da nossa estrutura. Para isso devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o engaste em D, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
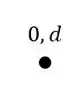
A partir desse ponto podemos marcar facilmente o ponto A, que desce 2 e anda 1 cm para esquerda, sendo assim o ponto A passa a ser.
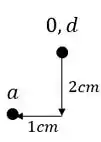
Como nem o ponto B e nem o ponto C estão ligados a dois pontos conhecidos, podemos achar um deles por suposição, e depois encontrar o outro.
O ponto B por exemplo, sabemos que ele desce 2 cm junto com o ponto A, porém apenas o ponto A segue 1cm para frente, já que a rótula em B fará a barra rotacionar e não deslocar em 1 cm. Dessa maneira podemos descobrir facilmente B no nosso williot descendo ele 2cm a partir do ponto indeslocavel, ou da origem, sendo assim teremos que:
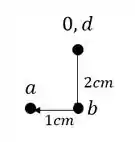
Agora a partir de B e de D podemos destemrinar o ponto C, basta traçarmos perpendiculares a cada uma das barras que se ligam a C, e a partir delas determinar o ponto de encontro no williot.
Fazendo isso teremos que:
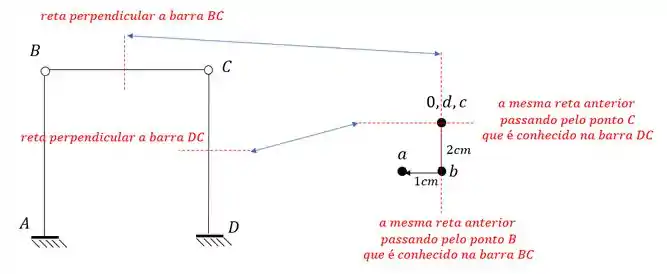
E assim determinamos o nosso wiliot completo que será dado por:
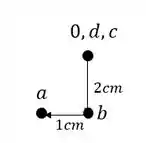
Passo 2
O williot nos ajudará a determinar os deslocamentos da estrutura devido ao recalque do apoio.
Mas para isso precisamos saber os números de hiperestáticos da nossa estrutura.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
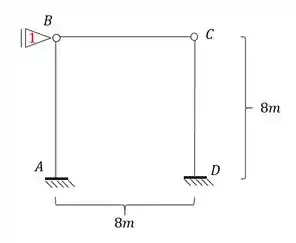
Passo 3
Tendo a deslocabilidade e o williot, podemos determinar o valor de . Como temos um apoio do primeiro gênero, temos que determinar as reações de apoio, e para isso precisamos determinar as deslocabilidades e momentos de cada barra, usando o nosso amigo williot teremos que:
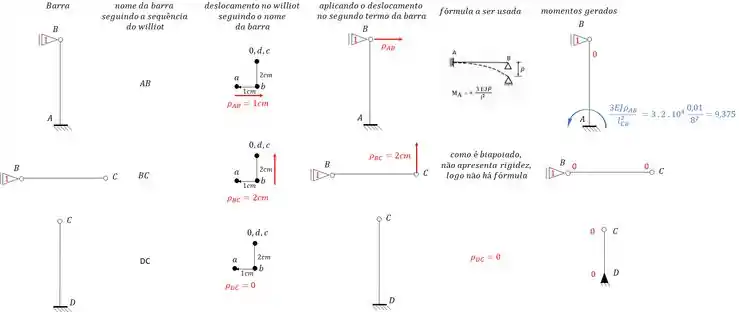
Perceba que somente uma barra será capaz de produzir reação de apoio. E essa reação de apoio que precisamos. Sendo assim teremos que:
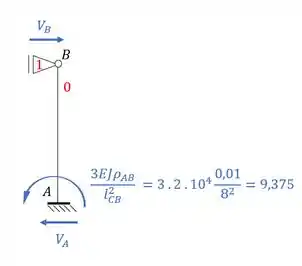
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 4
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
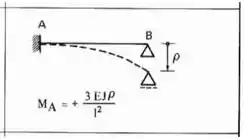
Fazendo esse deslocamento na nossa estrutura teremos que:
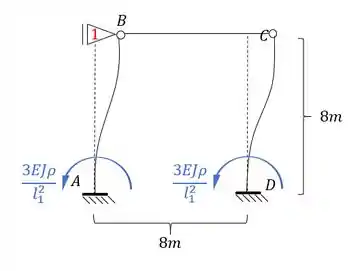
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
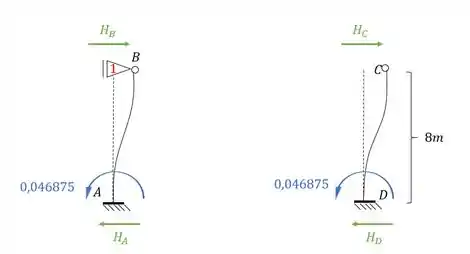
Perceba que precisamos dos valores de e . Com isso teremos que:
Mas lembre-se que . Sendo assim teremos que:
Passo 5
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #3
Origem do Exercício
A estrutura abaixo sofreu um recalque no apoio A de 5cm para baixo e 1 cm para esquerda. Sabendo disso determine o deslocamento horizontal do ponto B. use
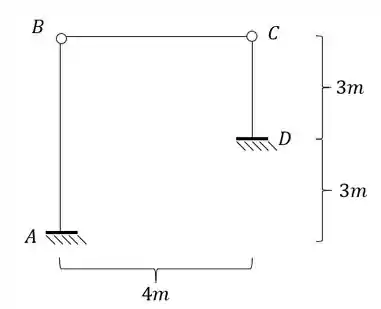
Passo 1
Para podermos determinarmos a deformação precisamos antes de tudo determinar o williot da nossa estrutura. Para isso devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o engaste em D, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
A partir desse ponto podemos marcar facilmente o ponto A, que desce 5 e anda 1 cm para esquerda, sendo assim o ponto A passa a ser.
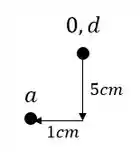
Como nem o ponto B e nem o ponto C estão ligados a dois pontos conhecidos, podemos achar um deles por suposição, e depois encontrar o outro.
O ponto B por exemplo, sabemos que ele desce 5 cm junto com o ponto A, porém apenas o ponto A segue 1cm para frente, já que a rótula em B fará a barra rotacionar e não deslocar em 1 cm. Dessa maneira podemos descobrir facilmente B no nosso williot descendo ele 5cm a partir do ponto indeslocavel, ou da origem, sendo assim teremos que:
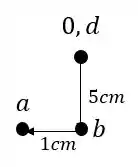
Agora a partir de B e de D podemos destemrinar o ponto C, basta traçarmos perpendiculares a cada uma das barras que se ligam a C, e a partir delas determinar o ponto de encontro no williot.
Fazendo isso teremos que:
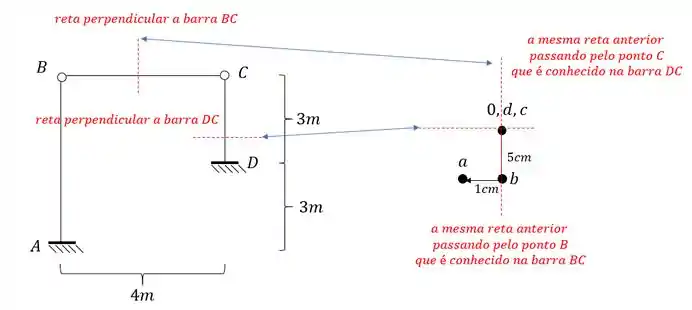
E assim determinamos o nosso wiliot completo que será dado por:
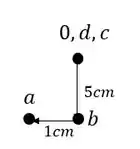
Passo 2
O williot nos ajudará a determinar os deslocamentos da estrutura devido ao recalque do apoio.
Mas para isso precisamos saber os números de hiperestáticos da nossa estrutura.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
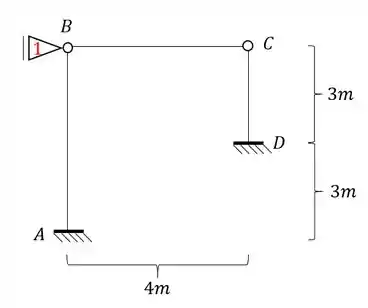
Passo 3
Tendo a deslocabilidade e o williot, podemos determinar o valor de . Como temos um apoio do primeiro gênero, temos que determinar as reações de apoio, e para isso precisamos determinar as deslocabilidades e momentos de cada barra, usando o nosso amigo williot teremos que:
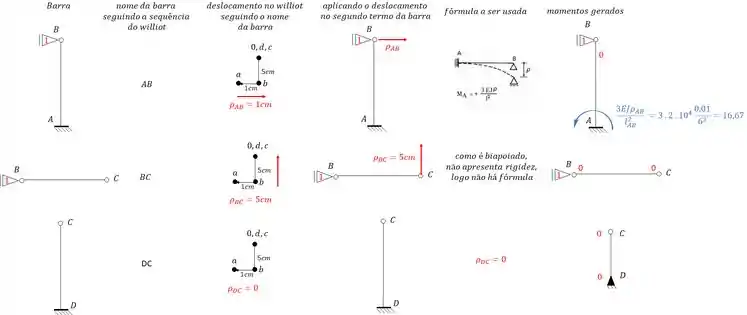
Perceba que somente uma barra será capaz de produzir reação de apoio. E essa reação de apoio que precisamos. Sendo assim teremos que:
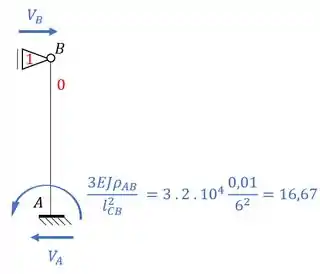
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 4
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
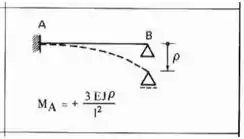
Fazendo esse deslocamento na nossa estrutura teremos que:
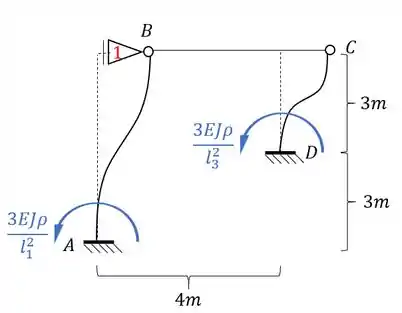
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
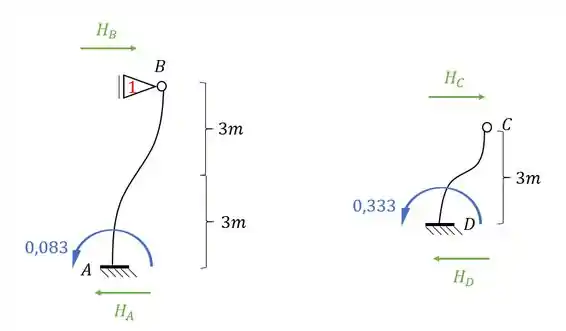
Perceba que precisamos dos valores de e . Com isso teremos que:
Para teremos que:
Passo 5
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #4
Origem do Exercício
A estrutura abaixo sofreu um recalque no apoio A de 5cm para baixo e 1 cm para esquerda. Sabendo disso determine o deslocamento horizontal do ponto C. use para as barras AB e CD .
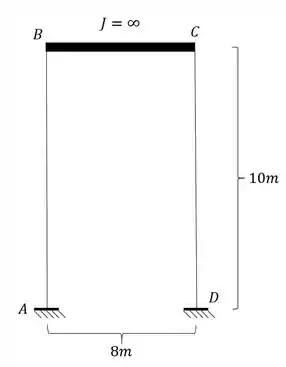
Passo 1
Para podermos determinarmos a deformação precisamos antes de tudo determinar o williot da nossa estrutura. Para isso devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o engaste em D, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
A partir desse ponto podemos marcar facilmente o ponto A, que desce 5 e anda 1 cm para esquerda, sendo assim o ponto A passa a ser.
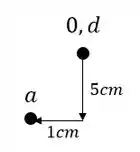
Como nem o ponto B e nem o ponto C estão ligados a dois pontos conhecidos, podemos achar um deles por suposição, e depois encontrar o outro.
O ponto B por exemplo, sabemos que ele desce 5 cm junto com o ponto A, porém apenas o ponto A segue 1cm para frente, pois supomos que a rigidez em B permite apenas que ele gire e não que ele se desloque, com isso teremos que:
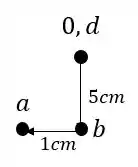
Agora a partir de B e de D podemos destemrinar o ponto C, basta traçarmos perpendiculares a cada uma das barras que se ligam a C, e a partir delas determinar o ponto de encontro no williot.
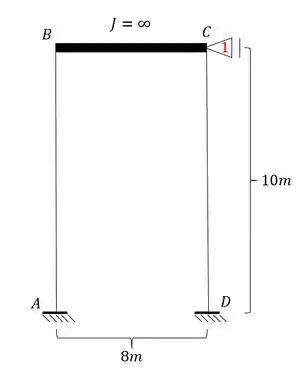
Fazendo isso teremos que:
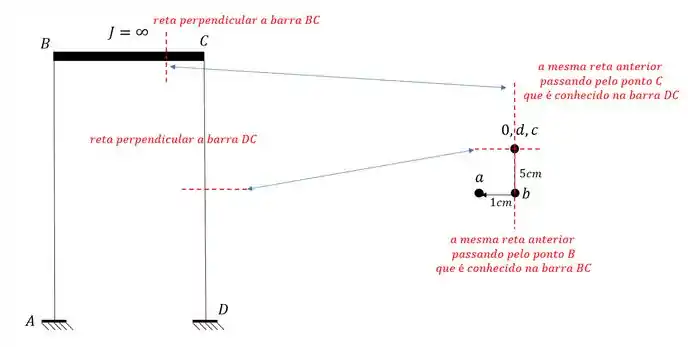
E assim determinamos o nosso wiliot completo que será dado por:
Passo 2
O williot nos ajudará a determinar os deslocamentos da estrutura devido ao recalque do apoio.
Mas para isso precisamos saber os números de hiperestáticos da nossa estrutura.
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
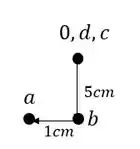
- Agora que vem o diferencial. Os pontos C e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós C e B não podem rotacionar porque a barra CB possui uma inércia tão grande que já vai impedir isso. Ou seja, não temos deslocabilidade interna.
- Analisando agora as deslocabilidades externas:
- Os pontos A e D são engastes, logo são considerados indeslocaveis.
- O ponto C também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto C travado podemos ver que passamos a ter o ponto B indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
Passo 3
Tendo a deslocabilidade e o williot, podemos determinar o valor de . Como temos um apoio do primeiro gênero, temos que determinar as reações de apoio, e para isso precisamos determinar as deslocabilidades e momentos de cada barra, usando o nosso amigo williot teremos que:
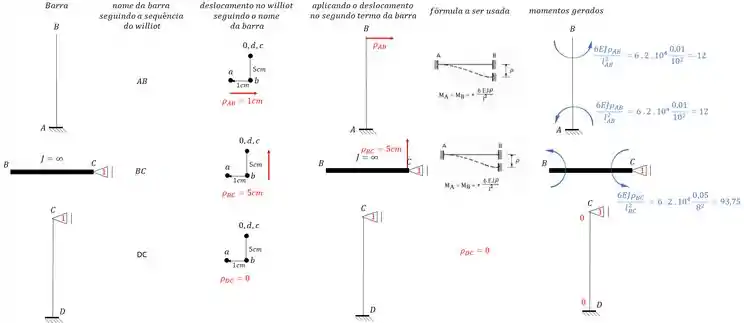
como queremos a reação em 1, somente a barra AB nós dará isso, com isso teremos que:
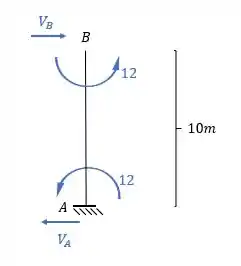
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 4
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 1.
Como temos que deslocar o nosso apoio em 1, e sabemos que todos os nossos nós são engastes, usaremos a seguinte fórmula:
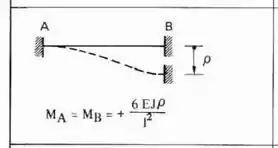
Colocando o deslocamento na nossa estrutura teremos que:
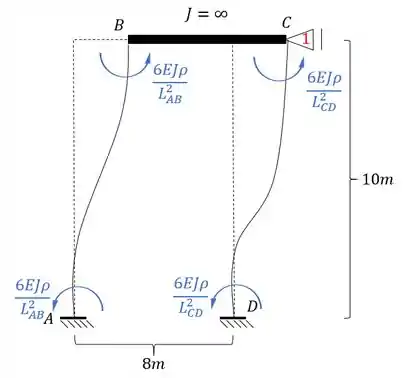
Usando o fator de rigidez relativa teremos que:
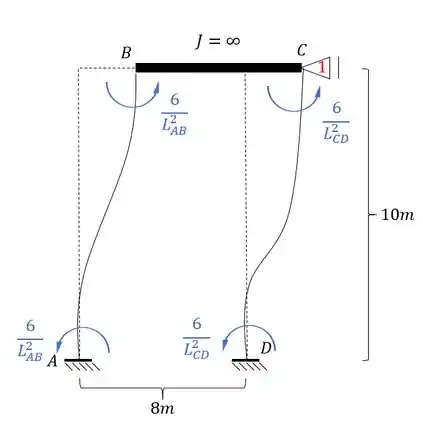
Como todos os comprimentos são iguais teremos que:
Veja que somente as barras AB e DC produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
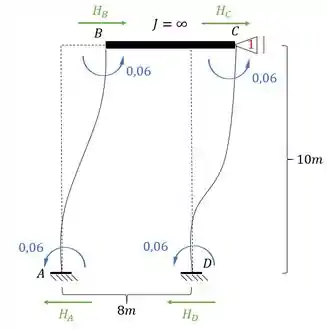
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 1, então a reação em 1 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 5
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #5
Origem do Exercício
O apoio em A da estrutura abaixo sofre um recalque vertical de 2cm e um recalque horizontal de 3cm. Sabendo disso determine o deslocamento horizontal do ponto B da estrutura. use
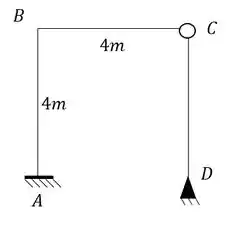
Passo 1
Aqui vamos usar um conceito novo. Para essa estrutura, sabemos facilmente que ela possuirá apenas 1 deslocabilidade interna no nó B, que iremos travar com uma chapa e teremos a seguinte estrutura:
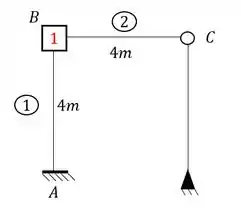
Porém perceba que o enunciado quer saber o quanto o ponto B irá se deslocar, ou seja, queremos saber o quanto o ponto B irá se movimentar, e sabemos que tudo que se movimenta no método dos deslocamentos deve ser travado. Ou seja, se queremos saber o quanto o ponto B irá se mover, devemos por nele um apoio do primeiro gênero, e com isso usa os conceitos de deslocabilidade da nossa estrutura para determinar o quanto ele de fato irá se mover.
Sendo assim teremos que:
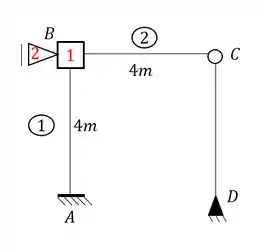
Perceba que a barra CD é bi-rotudada, ou seja, é como se fosse uma via bi-apoiada. O que significa isso? Significa que ela em nada vai contribuir nas nossas contas, ou seja, independente da deformação que ela tenha, ou da deformação imposta que façamos, a barra CD não vai contribuir nas contas, ou seja, uma simplificação que podemos fazer é:
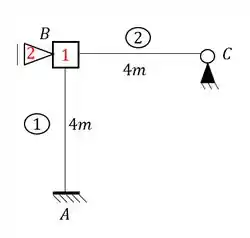
agora podemos continuar a conta ignorando essa barra, já que ela não vai contribuir em nada nas contas, e isso facilita os cálculos, a fórmula e o williot, então só temos a ganhar com isso, então bora lá.
Passo 2
Para podermos determinarmos a deformação precisamos antes de tudo determinar o williot da nossa estrutura. Para isso devemos marcar primeiro o ponto indeslocavel da nossa estrutura. Para isso sabemos que o indeslocavel é o ponot em C, porém o ponto que também seria indeslocável, que seria o ponto A, deixa de o ser devido ao deslocamento.
Com isso teremos que:
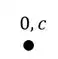
A partir desse ponto podemos marcar facilmente o ponto A, que desce 2 e anda 3 cm para esquerda, sendo assim o ponto A passa a ser.
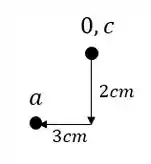
O ponto B vai ser achado a partir dos pontos A e C do nosso williot, usando o nosso conceito de ret perpendicular. Fazendo isso teremos que:
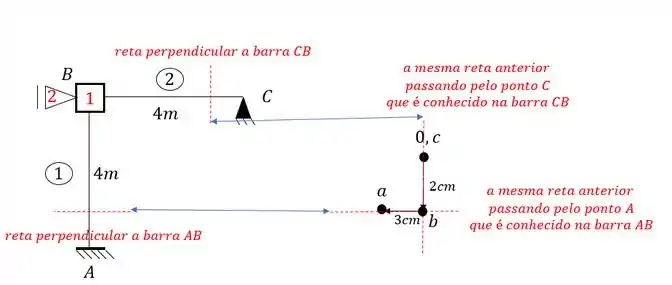
E assim determinamos o nosso wiliot completo que será dado por:
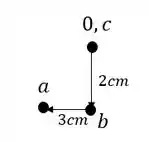
Passo 3
Tendo a deslocabilidade e o williot, podemos determinar o valor de . Como temos um apoio do primeiro gênero, temos que determinar as reações de apoio, e para isso precisamos determinar as deslocabilidades e momentos de cada barra, usando o nosso amigo williot teremos que:
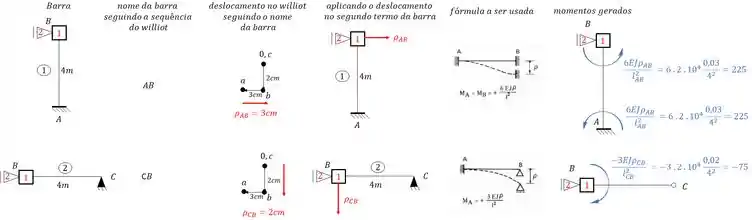
Os momentos que agem na chapa 1 iram gerar , sendo assim teremos que:
Perceba que somente uma barra (AB) será capaz de produzir reação de apoio na direaçaõ do apoio 2. E essa reação de apoio que precisamos para determinar . Sendo assim teremos que:
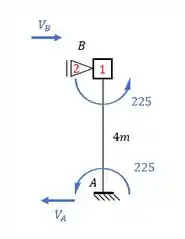
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 4
Vamos definir agora o valor de para termos o nosso sistema completo.
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso biengastado ou engastado e apoiado:
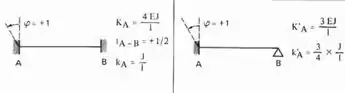
E rotacionando a chapa 1 e aplicando as equações teremos:
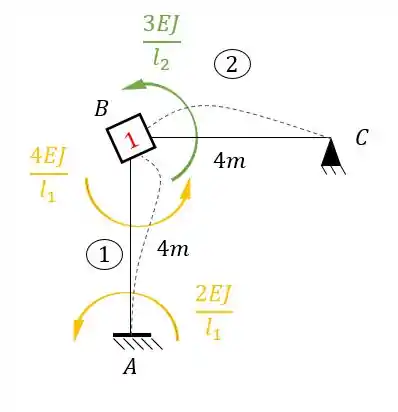
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Perceba que para determinar o valor de precisamos das reações de apoio que agem em 2. Podemos ver que de novo somente a barra AB produzira reações na direção horizontal, sendo assim teremos que:
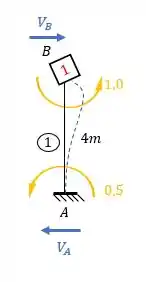
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Sabemos aqui que temos que deslocar o apoio em 2, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso biengastado ou engastado e apoiado:
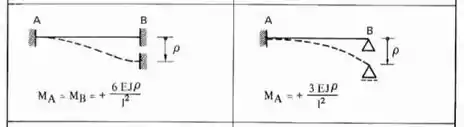
Causando o deslocamento teremos que:
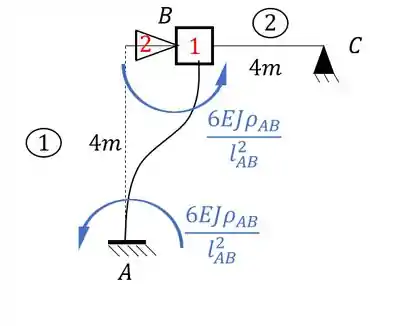
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E usando o valor de
E assim teremos:
Perceba que para determinar o valor de precisamos das reações de apoio que agem em 2. Podemos ver que de novo somente a barra AB produzira reações na direção horizontal, sendo assim teremos que:
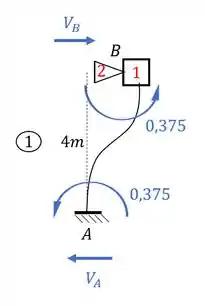
Precisamos do valor de .
Como a direção é para frente, a reação de apoio também será, e com isso teremos que:
Passo 5
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que: