Método dos deslocamentos no caso com deslocabilidade externa
Teoria
Introdução
Até aqui aprendemos como trabalhar com uma estrutura no caso em que ela só possua deslocabilidades internas.
Nessa aula vamos aprender o que fazer quando ela possuir uma deslocabilidade externa, ou seja, o que ocorre com aquele apoiozinho do primeiro gênero que colocamos nas nossas estruturas para representar a nossa deslocabilidade externa.
Já tivemos uma ideia do que fazer em uma estrutura que tem deslocamentos no nosso caso de williot, mas agora vamos ver como proceder no caso em que impormos um deslocamento unitário.
Deslocamento imposto
O funcionamento é exatamente o mesmo que temos no caso de deslocabilidade interna. Como fazíamos lá?
- Primeiro travávamos a rotação com uma chapa
- Depois rotacionávamos a chapa em 1 grau
- Em seguida analisávamos as condições de contorno
- Por fim fazíamos o calculo das rigidezes de cada nó de acordo com as condições de contorno
- Primeiro travamos o movimento com o apoio do primeiro gênero
- Depois deslocamos o apoio em uma unidade de comprimento
- Em seguida analisávamos as condições de contorno
- Por fim fazíamos o cálculo das rigidezes de cada nó de acordo com as condições de contorno
No caso da deslocabilidade externa, vamos seguir o mesmo passo a passo, mas fazendo o seguinte esquema.
Perceba que faremos a mesma coisa que antes, mas agora utilizando deslocamentos recíprocos, e não, rotações reciprocas, para isso vamos fazer um exemplo que vai nós auxiliar nos nossos cálculos.
Exemplo
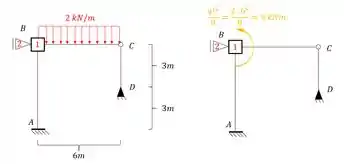
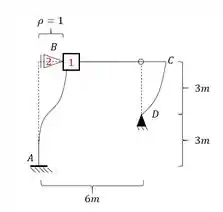
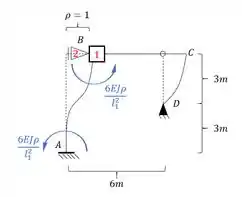
Imagine a estrutura abaixo, e imagine que a gente tenha que determinar as deformações verticais e rotacional do ponto B do desenho abaixo, como devemos proceder pra dar tudo certo? Usando .
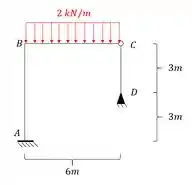
Passo 1 – determinar o as deslocabilidades e travar elas
Sabemos que para determinar as deslocabilidades precisamos seguir algumas regrinhas que já foram bem esmiuçadas nas aulas anteriores, então aqui vamos ir um pouco mais direto.
- Deslocabilidades internas
- Sabemos que são todos os nós que não são apoios extremos e nem rotulados
- Com isso temos que apenas o nó B será uma deslocabilidade interna, e por isso colocamos uma chapa nele.
- Deslocabilidades Externas
- Deslocabilidades externas são as que permitem algum deslocamento do nó além da rotação.
- No nosso caso o nó A e D são indeslocaveis
- O nó B é impedido de subir ou descer, mas pode ir pra frente ou para trás, dessa maneira, precisamos por ali um apoio do primeiro gênero, e com isso teremos que:
- Como o nó B se tornou indeslocavel, e o nó D já era, podemos dizer que o nó C também é indeslocavel.
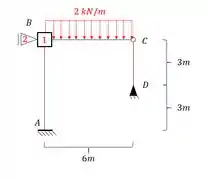
- A fórmula a ser usada é essa aqui em baixo:
- E a segunda coisa a ser notada é que esse deslocamento geralmente afeta mais de uma barra, por exemplo, perceba que a nossa barra AB foi dobrada, mas a nossa barra CD também foi dobrada. No nosso exemplo a barra CD por ser Bi-rotulada não apresentará momentos, mas só por isso que não iremos considerar momentos nela, se fosse outra barra com algum tipo de engaste, deveríamos considerar momentos em ambas as barras. Em vários exercícios iremos ver melhor isso, mas é importante já irmos com esse pensamento.
- Rotação do ponto B
- Deslocamento do ponto B
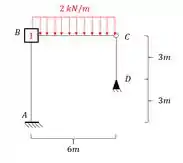
Dessa maneira montamos o nosso sistema a ser resolvido.
Passo 2 – determinar o valor de e
Para isso continuamos com a nossa tabelinha de momentos de engastamento perfeito, porém lembre-se que se para chapa determinamos momento, para apoios do primeiro gênero, teremos que determinar reações de apoio, sendo assim a nossa tabela a ser usada é:
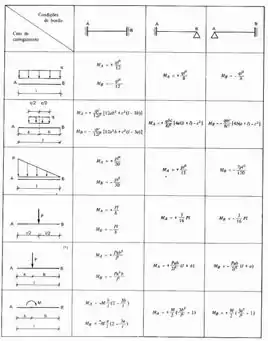
Perceba que só temos carregamento na barra BC, e que só temos carregamentos verticais, logo, como nosso apoio do primeiro gênero é horizontal, não teremos reação de apoio, e já podemos dizer que:
Mas vamos ver como determinar essas reações de apoio daqui a pouco.
Para determinar basta olharmos que em C o apoio é rotulado é no apoio B é engastado, então temos uma barra do tipo engastada e rotulada, e nossa conta será dada por:
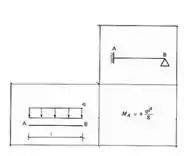
E assim a nossa fórmula será:
Assim sabemos que:
Passo 3 – determinar as reações de apoio
Nós determinamos as reações de apoio com intuito de determinar a reação no apoio do primeiro gênero, mas já vimos que nesse caso será zero, por isso vamos fazer aqui só um exemplo para sabermos resolver qualquer caso.
Para isso basta separarmos a barra do resto da estrutura, e lançar as reações de apoio como mostradas a seguir:
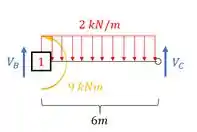
E perceba que as reações ficam na mesma direção das fibras tracionadas. Fazendo o somatório de momentos em B teremos que:
E como já deu positivo, o sinal pra reação de apoio se mantem positivo também. Se desse negativo, para reação de apoio também seria. E sempre faremos isso para determinar a reação de apoio, separamos as barras, calculamos os carregamentos e fazemos as reações de apoio, beleza? Bora continuar então.
Passo 4 – determinar o valor de e
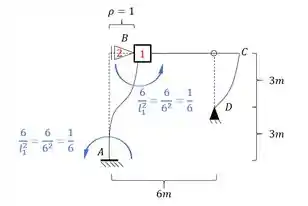
Perceba que agora começamos em um conceito que já conhecemos, como o segundo termo é 1, significa que temos que rotacionar a chapa 1, com isso teremos que dividindo esse termo por EJ, teremos que:
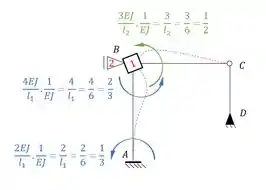
E lembre-se que sempre que rotacionamos uma chapa, usamos a seguinte equação:
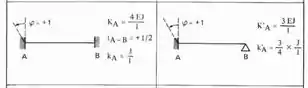
Dessa maneira teremos que:
Mas como determinamos o que acontece com ? Basta entender o que ele significa. Ele é o que acontece no apoio 2 devido a rotação na chapa 1, ou seja, precisamos das reações de apoio, fazendo o que já aprendemos, podemos fazer o seguinte:
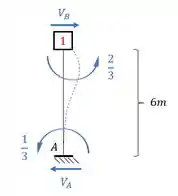
Fazendo o somatório de momentos em B teremos que:
Como o sinal se conserva pra reação de apoio, e precisamos do que está agindo na direção do apoio do primeiro gênero, usaremos o valor de no mesmo sentido que calculamos, ou seja, podemos dizer que:
Passo 5 – Determinar o valor de e
Agora que entra o nosso novo conceito, no passo anterior nós rotacionamos a nossa chapa em 2 grau certo? Mas agora não temos mais uma chapa, e sim um apoio, e nesse caso também iremos impor uma deformação, mas não mais de rotação, mas de deslocamento. Como decidimos que da esquerda para direita é positivo, iremos deslocar o nosso apoio do primeiro gênero da esquerda para direita e em uma unidade.
E sempre que deslocarmos um apoio devemos prestar aa tenção em duas coisas.
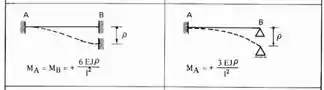
Dessa maneira teremos que:
Mas lembre-se que impomos uma deformação de , e devemos lembrar também que dividimos no outro caso tudo por EJ, então obrigatoriamente teremos que dividir por EJ também aqui, assim teremos:
Assim teremos que a rigidez que age no ponto 1 devido o movimento do apoio 2 será dado por:
E o que acontece no apoio 2 devido o movimento do apoio 2? É ai que determinamos as reações de apoio:
Como o sinal se conserva pra reação de apoio, e precisamos do que está agindo na direção do apoio do primeiro gênero, usaremos o valor de no mesmo sentido que calculamos, ou seja, podemos dizer que:
Passo 6 – Determinar as deformações
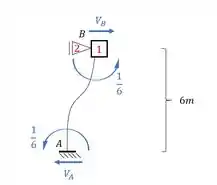
Agora é simples, todo o resto continua igual, o que acrescentamos aqui foi simplesmente como resolver um problema com deslocabilidade externa, e fazemos como sempre fazemos com a chapa, só que ao invés de rotacionarmos em um grau, deslocamos em uma unidade na horizontal, sendo assim teremos que apenas resolver o sistema gerado que será:
Resolvendo esse sistema teremos que:
E se pararmos para prestar a atenção vamos ver que representa a rotação do ponto B e o deslocamento horizontal do ponto B, que é exatamente o que a gente precisa. Mas devemos lembrar que simplificamos a nossa equação dividindo tudo por EJ, sendo assim, precisamos fazer isso aqui para termos os deslocamentos reais, e assim teremos que:
Se deu negativo é porque se rotacionamos a chapa no sentido anti-horário, significa que na realidade ela rotaciona no sentido horário.
Como deu positivo, significa que escolhemos o sentido certo, ou seja, da esquerda para direita.
Ou seja, com isso tudo, conseguimos entender como resolver problemas com deslocabilidade externa, e como determinar as suas deformações. E os momentos são determinados da mesma maneira que antes, podemos fazer da seguinte maneira:
Que substituindo teremos que:
E perceba que usamos os valores determinados no sistema, e não os valores das deformações reais, e com isso conseguimos resolver qualquer sistema com deslocabilidades externas, beleza? Bora fazer alguns exercícios para podermos ficar craques nessa área.
Deslocamento imposto
Exemplo
Passo 1 – determinar o as deslocabilidades e travar elas
Passo 2 – determinar o valor de β 10 e β 20
Passo 3 – determinar as reações de apoio
Passo 4 – determinar o valor de β 11 e β 21
Passo 5 – Determinar o valor de β 22 e β 12
Passo 6 – Determinar as deformações
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Para a estrutura abaixo, determine o deslocamento horizontal do ponto B do pórtico dado.
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de . Mas perceba que a carga de que age na vertical, não irá produzir reações de apoio na horizontal, então não precisamos nos preocupar com ela.
Em contra partida a carga concentrada de 10kN, irá produzir um momento no nosso apoio em A, e perceba que essa barra é engastada em A mas rotulada em B, ou seja, é do tipo engastada e rotulada, e sendo assim, a nossa equação será:
Aplicando ela na nossa estrutura teremos que:
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo, mas se você fizer o passo completo vai ver que faz sentido. Porque imagine se invertermos as reações, teríamos o seguinte:
Perceba que se invertermos os vetores, o sinal volta a ser positivo, porém veja que o sentido é para trás, e como vimos na teoria, para determinação de rigidez, consideramos pra frente positivo e pra trás negativo, com isso, o nosso valor de será:
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
Fazendo esse deslocamento na nossa estrutura teremos que:
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
Perceba que precisamos dos valores de e . Com isso teremos que:
Mas lembre-se que . Sendo assim teremos que:
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #2
Origem do Exercício
Para a estrutura abaixo, determine o deslocamento horizontal do ponto B do pórtico dado.
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que os pontos B e C são rótulas, logo, também não possuem deslocabilidades internas.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e D são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder subir ou descer devido o engaste em A, pode ir pra frente ou pra trás, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
- Como o ponto B acabou de se tornar indeslocavel, por consequência, o ponto C se torna indeslocavel também, e com isso passamos a ter apenas uma deslocabilidade na nossa estrutura.
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de . Mas perceba que a carga de que age na vertical, não irá produzir reações de apoio na horizontal, então não precisamos nos preocupar com ela.
Em contra partida a carga distribuída de , irá produzir um momento no nosso apoio em A, e perceba que essa barra é engastada em A mas rotulada em B, ou seja, é do tipo engastada e rotulada, e sendo assim, a nossa equação será:
Aplicando ela na nossa estrutura teremos que:
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo, mas se você fizer o passo completo vai ver que faz sentido. Porque imagine se invertermos as reações, teríamos o seguinte:
Perceba que se invertermos os vetores, o sinal volta a ser positivo, porém veja que o sentido é para trás, e como vimos na teoria, para determinação de rigidez, consideramos pra frente positivo e pra trás negativo, com isso, o nosso valor de será:
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
Fazendo esse deslocamento na nossa estrutura teremos que:
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações horizontais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
Perceba que precisamos dos valores de e . Com isso teremos que:
Para teremos que:
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento horizontal do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #3
Origem do Exercício
Para a estrutura abaixo, determine o deslocamento vertical do ponto B da estrutura abaixo.
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, fazendo isso teremos que:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e C são indeslocáveis, logo, não possuem deslocabilidade interna.
- Sabemos também que o ponto B é uma rótula, logo, também não possui deslocabilidade interna.
- Então já sabemos que não iremos por chapas na nossa estrutura
- Analisando agora as deslocabilidades externas:
- Veja que os pontos A e C são engastes, então não irão se deslocar, logo, também não temos deslocabilidades externas nesse ponto.
- Porém veja que o ponto B apesar de não poder ir para esquerda ou direita devido o engaste em A e B, pode ir pra cima ou para baixo, o que torna ele um ponto deslocavel, e sabemos que nesse tipo de caso precisamos travar esse movimento , especificamente com um apoio do primeiro gênero, dessa maneira teremos que:
Passo 2
Como só temos uma deslocabilidade, e essa deslocabilidade é um apoio do primeiro gênero, precisamos detemirnar a reação que age nele e essa reação será o valor de .
As cargas de 10 kN que irão causar as reações de apoio, dessa maneira teremos que usar a seguinte fórmula para o caso de carga concentrada e para condições de contorno do tipo engaste e apoio.
Precisamos analisar a contribuição de ambos os lados da viga:
Mas lembre-se que o que importa pra gente é a reação de apoio, e não necessariamente o momento, apesar de usarmos ele para determinação da reação de apoio. Dessa maneira teremos que:
Perceba que como quem age no nosso apoio fictício do primeiro gênero em 1 é o iremos usar ele para determinar a reação do nosso apoio.
Um macete legal para lembrarmos é que o que definimos para (modulo, sentido e direção) já vai valer para a reação que age em 1. Isso é para não precisar ficar transferindo carga, ou ficar pensando se tem que inverter a direção ou o sinal.
Absolutamente não, se der pra frente a reação é pra frente, se for pra baixo a reação é pra baixo, e assim em diante. Se der negativo, a reação será negativa, gravando assim fica mais fácil de lembrar, e com isso o nosso cálculo será:
Ou seja, o nosso valor de será negativo.
Passo 3
Agora só precisamos definir para termos o nosso sistema completo. Para isso sabemos que temos que deslocar o nosso apoio, e deslocando o apoio, usamos a seguinte fórmula:
Fazendo esse deslocamento na nossa estrutura teremos que:
Como fizemos um deslocamento imposto, podemos dar o valor que quisermos pra ele, que no nosso caso pode ser dado por:
Usando também o nosso conceito de rigidez relativa podemos dividir o nosso momento por EJ, e com isso restaria apenas:
Como temos o comprimento da barra fica fácil, e com isso teremos que:
E esse será o nosso valor de momento, mas qual é o nosso objetivo? É determinar a reação de apoio, porque vai ser a reação de apoio que vai nós dar o valor de . Mas temos que tomar cuidado, porque veja que temos momentos de ambos os lados, e ambos produziram reações verticais, e precisamos contabilizar a contribuição dos dois, sendo assim teremos que:
Perceba que precisamos dos valores de e . Com isso teremos que:
Como temos dois teremos no final que:
Passo 4
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Mas calma, não se assuste, esse ainda não é o deslocamento vertical do nosso ponto B. lembre-se que dividimos todos os fatores por EJ, ou seja, se quisermos saber o valor real, precisamos repor isso que tirarmos, dessa forma teremos que:
Resposta
Exercício Resolvido #4
Origem do Exercício
Para a estrutura abaixo, determine o diagrama de momentos fletores.
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, ms nessa estrutura temos que tomar um cuidado devido a barra de inércia infinita:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos E e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- O ponto C não é nem rótula e nem apoio extremo, logo possuirá uma deslocabilidade interna. E sabemos que se possuímos deslocabilidade interna, temos obrigatoriamente que travar ela com uma chapa, sendo assim teremos que:
- Agora que vem o diferencial. Os pontos A e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós A e B não podem rotacionar porque a barra AB possui uma inércia taõ grande que já vai impedir isso. Ou seja, só temos 1 deslocabilidade interna.
- Analisando agora as deslocabilidades externas:
- Os pontos E e D são engastes, logo são considerados indeslocaveis.
- O ponto C também pode ser considerado assim, além do mais, não pode nem se deslocar pra baixo e pra cima, e nem da esquerda para direita ou vice versa.
- O ponto B também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto B travado podemos ver que passamos a ter o ponto A indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
Passo 2
Sabendo as deslocabilidades e colocando os seus respectivos travamentos, agora já podemos começar a determinar as deformações do nosso problema.
Começando por e , teremos que:
Para determinação dele devemos olhar o nosso carregamento.
Perceba que o ponto A assim como o ponto C são como engastes, e a carga de 3kN age bem em cima do “engaste” em A. O que isso significa? Significa que nenhuma momento será produzido, e se não tem momento sendo produzido, não temos rigidez sendo produzida em 1 devido a carga de 3kN. Sendo assim, podemos imediatamente definir que:
E como não teremos momento sendo produzido em nenhum nó, podemos dizer que os momentos de todos os nós analisando da perspectiva de momento em 1 será.
Para determinação dele devemos olhar o nosso carregamento.
Agora a história é outra, precisamos determinar a reação que aparece no apoio 2. Perceba que a carga de 3kN age bem em cima dele e na mesma direção, ou seja, toda a carga será transferida diretamente pro apoio. Como no calculo de não tivemos nenhum momento fletor calculado, então podemos ficar tranquilos, pôquer assim sabemos que não haverá nenhuma outra contribuição agindo em 2. Se por acaso tivéssemos algum momento, então poderíamos analisar a contribuição dele. Como não tem, podemos ficar bem tranquilos e analisar apenas a reação de apoio que será.
Lembre-se que para reação de apoio consideramos para trás negativo e para frente positivo, dessa maneira temos que como a reação é para trás, consideraremos ela negativa, e com isso teremos que:
E como toda a carga se transfere para o apoio 2, a reação de apoio em todos os outros apoios e pontos será zero.
Passo 3
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Sabemos que para definir é muito simples, como se trata de uma chapa, basta rotacionarmos ela em 1 grau, que sempre rotacionamos no sentido anti-horário para sempre termos esse valor positivo.
Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:
Fazendo isso na nossa estrutura teremos que:
Sendo assim o valor de será:
Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:
Sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.
Veja que somente as barras EC e CA produziram reações na horizontal. Porém apenas a barra CA irá interferir no nosso apoio em 2, por isso iremos calcular apenas a reação de apoio referente a ela, sendo assim teremos que:
Marcando as reações teremos que:
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se está pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 4
Agora que definimos as rigidezes do sistema 1, precisamos determinar no sistema 2. Como o sistema 2 é um apoio iremos precisar usar o conceito de deformação e não amis de rotação.
Sabemos que para definir é muito simples, como se trata de uma chapa, basta analisarmos o momento que aparecerá nela após a deformação de 1 unidade.
Como todas as extremidades são engastadas, e até mesmo os pontos A e B representam engastes, então teremos que a fórmula a ser usada é:
Fazendo o deslocamento na nossa estrutura teremos que:
Sendo assim o valor de será:
Sabemos que podemos usar rigidez relativa para facilitar as nossas contas, que podemos usar:
E também podemos usar que:
Sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 2.
Veja que somente as barras CA e DB produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 2, então a reação em 2 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 3
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Para determinação dos momentos precisamos do valor de momento fletor em cada ponto de cada sistema que analisamos, ou seja:
Como já determinamos os valores de e basta determinarmos os momentos usando a seguinte fórmula:
Substituindo teremos que:
Calculando os momentos teremos que:
Fazendo o momento teremos que:
Resposta
Exercício Resolvido #5
Origem do Exercício
Para a estrutura abaixo, determine o diagrama de momentos fletores.
Passo 1
Como já sabemos o nosso primeiro passo deve ser obrigatoriamente determinar o número de deslocabilidades da nossa estrutura, ms nessa estrutura temos que tomar um cuidado devido a barra de inércia infinita:
- Analisando primeiro as deslocabilidades internas:
- Sabemos que os pontos A e D são indeslocáveis, logo, não possuem deslocabilidade interna.
- Agora que vem o diferencial. Os pontos C e B estão nas extremidades da barra com inércia infinita. SEMPRE que tivermos uma barra com inércia infinita, ela obrigatoriamente tornará os nós da sua extremidade indeslocaveis com relação a rotação. Ou seja, os nós C e B não podem rotacionar porque a barra CB possui uma inércia tão grande que já vai impedir isso. Ou seja, não temos deslocabilidade interna.
- Analisando agora as deslocabilidades externas:
- Os pontos A e D são engastes, logo são considerados indeslocaveis.
- O ponto C também não pode se deslocar na vertical, porém pode claramente se deslocar na horizontal, por isso devemos travar ele nesse sentido, com o nosso velho amigo apoio do primeiro gênero.
- Com o ponto C travado podemos ver que passamos a ter o ponto B indeslocavel, logo teremos apenas 1 deslocabilidade externa mesmo.
Passo 2
Sabendo as deslocabilidades e colocando os seus respectivos travamentos, agora já podemos começar a determinar as deformações do nosso problema.
Começando por , teremos que:
Para determinação dele devemos olhar o nosso carregamento.
Perceba que precisamos determinar a reação de apoio, e para determinar a reação de apoio precisamos determinar os momentos. A carga age na barra AB. Sabemos que o ponto A é um engaste, e que o ponto B é a extremidade de uma barra com inércia infinita, ou seja, também é um engaste. Sendo assim teremos que a fórmula a ser usada é:
Porém como o que precisamos são as reações de apoio em 1, teremos que:
Precisamos da reação que está na mesma direção do apoio, ou seja , e vale lembrar que o sentido da força já irá nos dar o sentido da reação, sendo assim teremos que:
Mas perceba que a força deu para traz, e na nossa perspectiva de sinais, sempre que ela da para trás, para a rigidez do ponto, consideramos ela negativa, sendo assim teremos que:
Os momentos nesse caso serão:
Passo 3
Agora que definimos as rigidezes do sistema zero, precisamos determinar nos sistemas com a deformação de cada um dos travamentos, sendo assim teremos que:
Para determinar o valor é muito simples, é só determinarmos a reação de apoio que age no nosso ponto 1.
Como temos que deslocar o nosso apoio em 1, e sabemos que todos os nossos nós são engastes, usaremos a seguinte fórmula:
Colocando o deslocamento na nossa estrutura teremos que:
Usando o fator de rigidez relativa teremos que:
Como todos os comprimentos são iguais teremos que:
Veja que somente as barras AB e DC produziram reações na horizontal, por isso iremos calcular apenas a reação de apoio referente a elas, sendo assim teremos que:
E aqui temos uma diferença importante, o sentido da reação nesse caso, é o mesmo da força calculada, ou seja, se e estão pra frente, e na mesma direção do apoio 1, então a reação em 1 vai ser pra frente também e com o mesmo valor de . Sendo assim teremos que:
Passo 3
Resolvendo o nosso sistema vamos ter que:
Substituindo teremos que:
Para determinação dos momentos precisamos do valor de momento fletor em cada ponto de cada sistema que analisamos, ou seja:
Como já determinamos o valorer de basta determinarmos os momentos usando a seguinte fórmula:
Substituindo teremos que:
Calculando os momentos teremos que:
Por fim temos que lembrar que nos temos uma barra com uma força concentrada no meio da barra, nesse caso precisamos fazer um diagrama de momentos considerando a barra biapoiada, dessa maneira teremos que:
Perceba que na barra AB ainda usamos o conceito de momento triangular para barras com carga concentrada.
Resposta
