Método das forças – O sistema de equações e incógnitas
Produzido por Pablo RicardoTeoria
Introdução
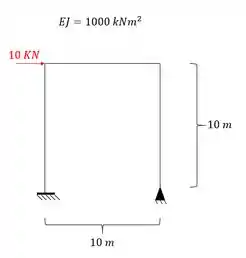
O método das forças será usado para determinação do diagrama de momentos, reações de apoio, diagrama de cortantes e normais, tudo isso, em estruturas hiperestáticas. Como vimos até aqui, descobrimos como calcular tudo isso em estruturas isostáticas. Mas agora com esse esquema vamos aprender a fazer isso nas estruturas hiperestáticas.
Conceito
O conceito em si não é muito complicado, mas é necessário ter muito cuidado na hora de executá-lo. Para ficar bem simples, vamos resolver um exemplo numérico para que assim possamos entender bem como podemos resolver o nosso problema.
Suponha que você tenha que definir as seguintes coisas com relação a essa estrutura:
- Graus de hiperestaticidade
- Reações de apoio
- Diagrama de momentos fletores
Agora vamos ver no nosso passo a passo como usar o método das forças.
Passo 1
Você já deve imaginar que resolver problemas isostáticos é mais fácil do que hiperestáticos, não é mesmo? O nosso conceito hoje é transformar uma estrutura hiperestática em uma estrutura isostática. Para eu saber o que a minha estrutura hiperestática precisa para se tornar isostática, eu preciso saber qual o grau de hiperestaticidade da nossa estrutura. Então vamos lá:
- Hiperestáticos totais pelo macete
- Sabemos que temos 1 apoio do terceiro gênero e 1 do segundo gênero, totalizando 5 incógnitas externas
- Não temos regiões fechadas, totalizando 0 incógnitas internas
- Temos 3 equações de equilíbrio
- Não temos rótulas
- Sistema zero
- Ponto 1
- Ponto 2
Ou seja, nossa estrutura possui dois graus de hiperestaticidade, que se eu conseguir tirar da nossa estrutura, transforma a nossa estrutura em isostática. E bem, é exatamente isso que vou fazer, e é ai que mora o segredo, podemos quebrar quaisquer dois vínculos da nossa estrutura, desde que ela fique isostática.
Passo 2
Como eu disse, podemos quebrar dois vínculos da estrutura, e substituir esses vínculos por hiperestáticos de reação, sacou a jogada? Eu tiro o vinculo para a estrutura se tornar isostática, mas coloco uma reação, relacionada àquele vinculo quebrado, exatamente para que a estrutura continue se mantendo de maneira coerente, e como disse, podemos quebrar quaisquer dois vínculos que a nossa estrutura tenha, como o exemplo abaixo.
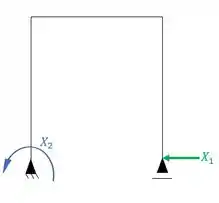
Perceba que eu quebrei um vínculo do apoio do segundo gênero da direita que travava deslocamento horizontal, e no lugar coloquei um hiperestático, que chamei de X1 no lugar.
No apoio do terceiro gênero da esquerda, quebrei um vinculo de momento, e coloquei no lugar um hiperestático que compensasse a quebra que fiz, ou seja, coloquei um hiperestático de momento que chamei de X2. E agora eu tenho uma estrutura isostática com ação de dois hiperestáticos nela.
E perceba que eu poderia por exemplo, quebrar dois vínculos do apoio de terceiro gênero e passar a ter um apoio do primeiro gênero na esquerda e um do segundo gênero na direita. Ou quebrar os dois vínculos do apoio do segundo gênero da direita e ter apenas um apoio do terceiro gênero. Eu tenho inúmeras possibilidades, e todas darão a mesma resposta e seguirão o mesmo passo a passo, beleza? Então bora prosseguir.
Passo 3
O sistema isostático que definimos no passo anterior é muito importante, porque agora tudo vai girar em torno dele. Porque pensa no seguinte: antes nós tínhamos um sistema hiperestático todo travado e que não conseguíamos resolver, agora, temos um sistema em que liberamos alguns movimentos, mas travamos por força. No entanto, lembre-se que por exemplo, todo movimento que houver na horizontal, na estrutura isostática, no ponto 1 (ponto em que está o hiperestático 1) na verdade não existe na estrutura hiperestática.
Então é ai que reside o cuidado que vamos ter que tomar com a nossa equação. Primeiro temos que definir o número de sistemas que temos, e é bem fácil, é simplesmente o número de hiperestáticos +1 ( esse +1 é o próprio sistema principal com o carregamento do enunciado).
No nosso caso temos 3 sistemas que são:
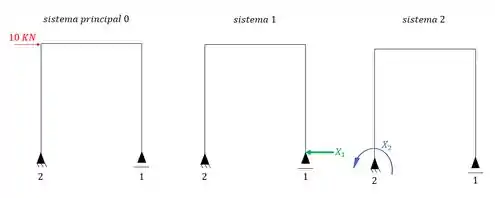
Perceba que o sistema principal zero, possui apenas o carregamento, o sistema principal 1, possui apenas o hiperestático 1, e o sistema principal 2, possui apenas o hiperestático 2. E perceba que os ponto que tem os hiperestáticos eu chamei de 1 e 2 em todos os sistemas, isso você vai ver que facilita muito a nossa vida, e agora é que vem o passo maneiro.
Passo 4
Lembra que no passo anterior eu disse que na estrutura isostática nos vamos permitir movimentos que não deveriam ser permitidos? Vamos mapear esses movimentos que não existiam e passaram a existir, em cada um dos sistemas, e pra isso é bom saber como vamos nomear isso, que é da seguinte maneira:

Por exemplo:
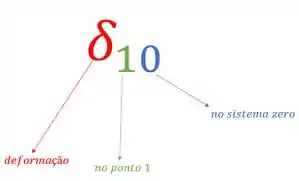
Feito isso, se fizermos o mapeamento teremos que:
- Passo 5
E pensa comigo, eu tenho que garantir que quando eu juntar todos os sistemas, tudo que ocorrer na junção dos sistemas deve ocorrer no sistema único hiperestático, e pra fazer isso eu só preciso resolver mais uma coisa. Eu sei quanto que vale e porque eu tenho os carregamentos do sistema 0, mas quanto valem as outras deformações? Eu não faço ideia, mas eu sei o seguinte, se eu analisar os meus hiperestáticos X1 e X2 como sendo valores unitários agindo na minha estrutura, eu consigo determinar o valor de para uma carga unitária, e com isso basta eu fazer a deformação para uma carga unitária, multiplicada para a carga real, que eu tenho a deformação real. Tá, talvez possa ter parecido embolado, mas é isso aqui que quero dizer:
- Para o ponto 1
- Para o ponto 2
- Passo 6
- Fique ligado
- 1 hiperestático
- 1 equação
- 2 termos
- 2 hiperestático
- 2 equação
- 3 termos
- 3 hiperestático
- 3 equação
- 4 termos

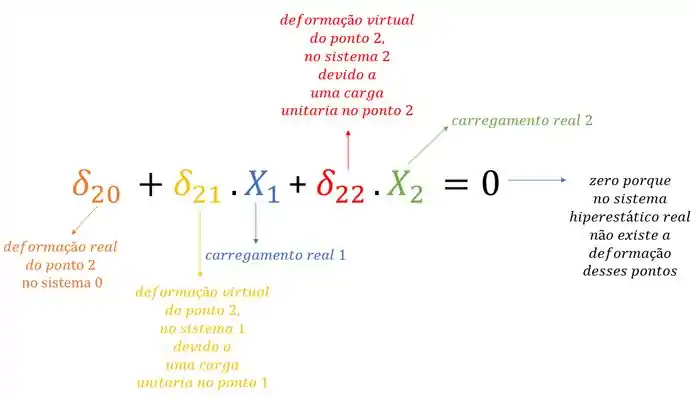
E perceba que o número de equações sempre vai ser igual ao número de hiperestáticos.
Logo o nosso sistema de equações para esse problema será:
E desse sistema precisamos tirar os valores de X1 e X2, ou seja, o método das forças vai nos das as forças dos vínculos que quebramos na nossa estrutura, mas o que você pode estar na dúvida agora é, se o objetivo é determinar X1 e X2, como raios vamos determinar os valores de ?
É exatamente isso que vamos ver na parte II de método das forças, nessa parte 1 aprendemos como determinar o sistema de equações que resolve o nosso problema.
É muito importante perceber que o número de equações e termos varia com o número de graus de hiperestaticidade.
O número de equações sempre vai ser dado pelo número de incógnitas, ou melhor, pelo numero de hiperestáticos.
Já o número de termos por fórmula será dado pelo numero de hiperestáticos +1, em resumo vamos ter isso aqui.
E agora, tendo entendido como é bem tranquilo montar o nosso sisteminha a ser resolvido, bora fazer mais exercícios pra ficar craque em Montar o nosso sistema, e quando já estivermos bem treinado nisso, vamos para parte 2 dessa aula que vai mostrar como resolver o sistema.