Método de williot para temperatura
Teoria
Introdução
Aprendemos que o método de williot é um método que nos ensina a determinar os deslocamentos na nossa estrutura, e o nosso objetivo nessa aula é entender exatamente como determinar os deslocamentos a partir de variações de temperatura.
O que é importante deixarmos claro é que a temperatura, assim como o recalque, são carregamentos da estrutura, ou seja, o williot vai nos auxiliar a calcular os valores de , , ... e assim por diante.
Já os valores de , , ... serão determinados usando o nosso conceito de rotação ou deslocamentos impostos, ou seja, essa parte a gente sempre vai fazer igual.
A primeira parte que temos que tomar muito cuidado quando formos fazer, ou usando um carregamento externo, ou o williot de recalque, ou como vamos ver nessa aula o Williot de temperatura.
Determinando as temperaturas.
Uma coisa legal de fazermos é aprendermos a usar a nossa temperatura. Sabemos que temos 3 conceitos importantes de temperatura.
- Temperatura nas fibras superiores (ou externas) -
- Temperatura no centro de gravidade -
- Temperatura nas fibras inferiores (ou internas) -
- Exemplo
- Caso em que
Imagine que no nosso problema seja dito que a temperatura das fibras superiores (ou externas) seja de +50°C e a temperatura das fibras inferiores (ou internas) seja de +10°C.
Se desenharmos isso teremos que:
Porém perceba que parece ser muito complicado trabalhar com a estrutura dessa maneira, por isso, podemos fazer o seguinte.
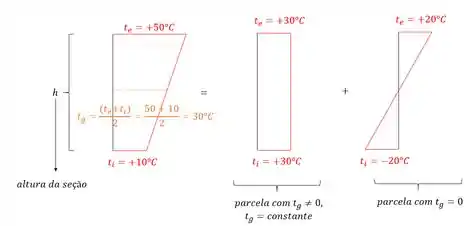
Porque fazemos essa distinção? Porque agora ficamos com duas parcelas fáceis de trabalhar, uma sem e outra com um constante. Como geralmente o era nosso problema, com essa divisão conseguimos facilitar a nossa vida, e para cada parcela vamos ter um método de solução.
Começamos com esse caos porque é bem simples calcularmos as rigidezes dele. Basta usarmos as seguintes fórmulas:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Caso em que
- Determinação da origem do Williot
- Determinação do ponto seguinte.
- Tendo C e E podemos determinar F
- Tendo B e D podemos determinar D
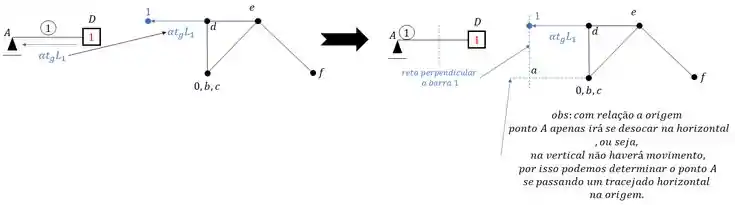
- Tendo o ponto D determinasse A
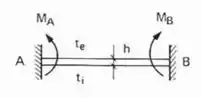
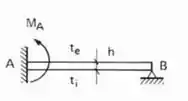
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
Mas e se a das externas for maior? Ai é muito simples, vai simbolizar que na verdade os momentos são no outro sentido.
Ou seja, se temos , basta sabermos se e as fórmulas de acordo com as condições de contorno, e tomando cuidado com os sinais e sentidos dos momentos, determinamos bem tranquilamente as rigidezes ( , , ...) para o caso com .
Agora que temos que tomar bastante cuidado, porque agora que vamos aprender a usar o nosso williot pata temperatura.
Vamos primeiro entender como montar o williot e depois podemos ver como aplicar ele, para isso vamos usar como exemplo a estrutura abaixo que já tem as chapas postas nos seus nós.
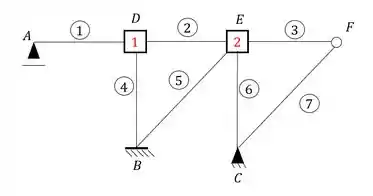
A origem do Williot sempre será marcada por um 0 e junto com esse zero ficaram (em letra minúscula) os pontos indeslocáveis da nossa estrutura, que no nosso exemplo são os pontos B e C, sendo assim teremos.
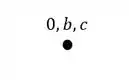
E a partir dessa origem iremos determinar os nossos pontos, que obviamente tenham algum contato com a nossa origem, porem devemos tomar cuidado com a forma de fazer isso.
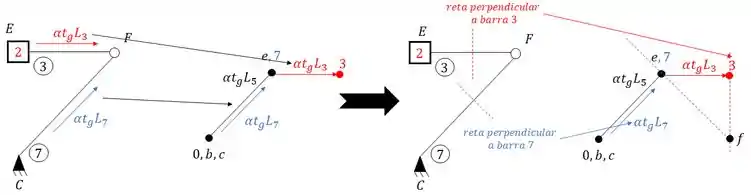
Perceba que temos na nossa origem o ponto B e C, ou seja, podemos usar esses dois pontos para determinar o ponto E.
Para isso a primeira coisa que devemos fazer é determinar o deslocamento tanto da barra que possui B e E (barra 5) quanto a barra que possui C e E (barra 6), e quando temos variação de temperatura, sabemos que a fórmula da dilatação será dada por:
E agora o primeiro cuidado, marcamos essas deformações no mesmo sentido da barra, e o ponto que vamos determinar chamaremos pelo próprio nome das respectivas barras, e com isso vamos ter que:
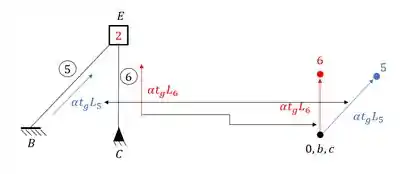
Perceba que no fim de cada deformação colocamos o próprio numero da barra, porque? Já vamos descobrir.
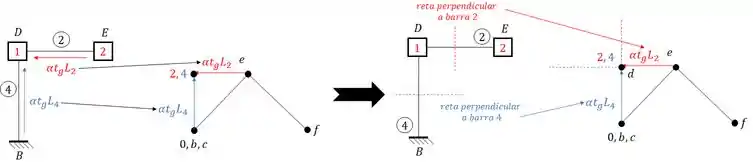
Agora é só fazermos oque aprendemos no williot de recalque, traçamos uma perpendicular em cada uma das barras e levamos elas até o nosso williot. E onde vamos passar essas retas perpendiculares? Exatamente nos pontos com o número das barras relacionadas, por isso colocamos o numero da barra, pra facilitar exatamente isso, ou seja, teremos que:
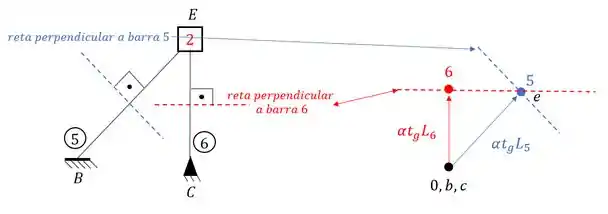
Ou seja, podemos escrever o nosso atual williot como:
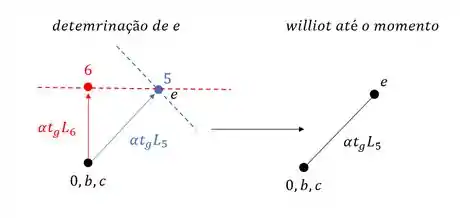
O ponto de encontro entre as retas perpendiculares as barras é exatamente o nosso ponto E, e se prosseguirmos assim, podemos montar o nosso wiliot da seguinte maneira:
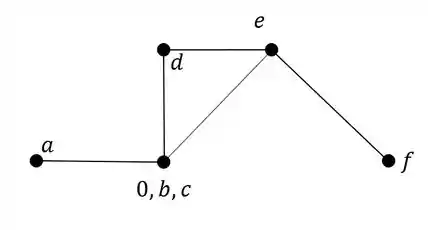
Se tirarmos todos os números, o nosso williot seria:
se mantivermos os números temos o nosso williot completo, que geralmente é o williot que o professor quer que você faça, dessa maneira teremos que:
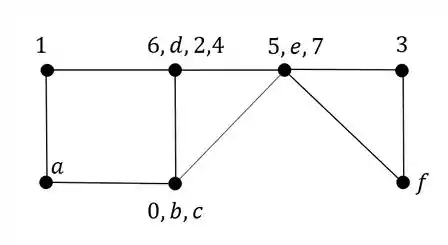
Mas de maneira geral, sempre mantenha os números, porque mantendo eles, conseguiremos determinar os deslocamentos da nossa barra. Mas isso vai ser assunto para a nossa próxima aula, vamos manter por enquanto nessa aqui apenas a maneira que descobrimos e montamos o nosso williot. Bora fazer exercícios então.
Determinando as temperaturas.
Exercícios Resolvidos
Exercício Resolvido #1
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A e C são indeslocáveis
- Sendo assim, o ponto B também será considerado indeslocavel
- Dessa maneira não temos deslocabilidades externas
- Mas o ponto B pode rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 1 deslocabilidade interna
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
Passo 2
Determinado tudo isso vamos definir o valor de .
Para isso temos que olhar o que acontece com a nossa barra. Sabemos que a barra AB apresenta um engaste em uma ponta e uma chapa na outra, sendo assim, podemos considerar ela bi-engastada, e para a barra bi engastada a equação é:
Mas a barra está em pé, o que faremos? Basta vira a figura.
E assim podemos aplicar as nossas fórmulas, que serão:
Para a barra BC, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
E aplicando isso a nossa estrutura teremos que:
E assim na nossa estrutura, os momentos que agem na chapa e que geram a sua rigidez, são dados por:
E assim teremos que:
Passo 3
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
- Sistema 0
- Sistema 1
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso biengastado ou engastado e apoiado:
E rotacionando a chapa 1 e aplicando as equações teremos:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 3
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, sendo assim teremos que:
E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
Resposta
Exercício Resolvido #2
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A e C são indeslocáveis
- Sendo assim, o ponto B também será considerado indeslocavel
- Dessa maneira não temos deslocabilidades externas
- Mas o ponto B pode rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 1 deslocabilidade interna
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
Passo 2
Determinado tudo isso vamos definir o valor de .
Tanto para a barra AB quanto para a barra BC, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essas barras do tipo engastada e apoiada, e a fórmula a ser usada nela é:
E aplicando isso a nossa estrutura teremos que:
Assim teremos que a rigidez total em B será dado por:
Passo 3
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
- Sistema 0
- Sistema 1
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1 e 2 respeitando o caso engastado e apoiado:
E rotacionando a chapa 1 e aplicando as equações teremos:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 5
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, sendo assim teremos que:
E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
Resposta
Exercício Resolvido #3
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine o diagrama de momentos fletores da mesma.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A, B e C são indeslocáveis
- Sendo assim, o ponto D também será considerado indeslocavel
- Dessa maneira não temos deslocabilidades externas
- Mas o ponto D pode rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 1 deslocabilidade interna
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
Passo 2
Determinado tudo isso vamos definir o valor de .
Sabemos que tanto a barra AD quanto a barra DC apresentam um engaste em uma ponta e uma chapa na outra, sendo assim, podemos considerar elas bi-engastadas, e para a barra bi engastada a equação é:
Mas a barra está em pé, o que faremos? Basta vira a figura.
E assim podemos aplicar as nossas fórmulas, que serão:
Para a barra DC, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
E aplicando isso a nossa estrutura teremos que:
Olhando a estrutura com todos os momentos teremos que:
Assim teremos que a rigidez total em D será dado por:
Passo 3
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
- Sistema 0
- Sistema 1
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 1, 2 e 3 respeitando o caso engastado e apoiado e o caso Bi-engastado:
E rotacionando a chapa 1 e aplicando as equações teremos:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Substituindo teremos que:
Passo 3
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Para determinação dos momentos fletores, precisamos do momento fletor de todos os nós em todas as barras em todos os sistemas, dessa forma a primeira coisa que devemos fazer é analisar cada sistema.
Uma coisa mega importante é lembrar de usar o fator de rigidez relativa EM TODOS OS CASOS que temos para o sistema 1, se não vamos errar, sendo assim teremos que:
E usando a nossa fórmula para cada nó teremos que:
Perceba que já temos os momentos de cada nó da nossa estrutura, e para cada barra, sendo assim se desenharmos isso na nossa estrutura teremos que:
Resposta
Exercício Resolvido #4
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a rotação dos pontos B e C.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A, E e D são indeslocáveis
- Sendo assim, os pontos B e C também serão considerados indeslocaveis.
- Dessa maneira não temos deslocabilidades externas
- Mas os pontos B e C podem rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 2 deslocabilidades internas
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
Passo 2
Determinado tudo isso vamos definir o valor de .
Sabemos que tanto a barra AD quanto a barra DC apresentam um engaste em uma ponta e uma chapa na outra, sendo assim, podemos considerar elas bi-engastadas, e para a barra bi engastada a equação é:
Mas a barra está em pé, o que faremos? Basta vira a figura.
Assim podemos aplicar essa fórmula nas seguintes barras:
- AB
- BC
- CE
Fazendo isso teremos que:
Como essa fórmula independe do comprimento, podemos calcular uma das equações e depois substituir na estrutura respeitando o sinal.
Substituindo na estrutura teremos que:
Para a barra CD, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
E aplicando isso a nossa estrutura teremos que:
Perceba que para respeitar a regrinha de o momento sempre sair das fibras inferiores e ir pra superiores, nós invertemos o sentido do momento para ficar tudo certinho.
Substituindo na fórmula teremos que
Olhando a estrutura com todos os momentos teremos que:
Assim teremos que a rigidez total em D será dado por:
Passo 3
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
- e
- e
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
E rotacionando a chapa 1 e aplicando as equações teremos:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Passo 5
Determinando o resto do sistema teremos que:
Sabemos aqui que temos que rotacionar agora a chapa 2, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
E rotacionando a chapa 2 e aplicando as equações teremos:
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Passo 4
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Perceba que os valores de deformações calculados já são as deformações de rotação dos pontos pedidos no enunciado, ou seja, o ponto B (referente a ) e o ponto C (referente a .
Porém tome cuidado, porque para calcularmos essas deformações usamos um conceito de rigidez relativa, que é exatamente o fatorzinho que usamos pra facilitar o cálculo, que é dado por:
Então basta usarmos esse fator para descobrirmos a deformação verdadeira:
Resposta
Exercício Resolvido #5
Origem do Exercício
Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a rotação dos pontos B, C e D.
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A, F, G e E são indeslocáveis
- Sendo assim, os pontos B, C e D também serão considerados indeslocaveis.
- Dessa maneira não temos deslocabilidades externas
- Mas os pontos B, C e D podem rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 3 deslocabilidades internas
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
Passo 2
Determinado tudo isso vamos definir o valor de .
Sabemos que tanto a barra AB quanto as barras BC, CD e DE apresentam um engaste em uma ponta e uma chapa na outra, ou ainda chapa em ambas as pontas, sendo assim, podemos considerar elas bi-engastadas, e para a barra bi engastada a equação é:
Mas a barra está em pé, o que faremos? Basta vira a figura.
Assim podemos aplicar essa fórmula nas seguintes barras:
- AB
- BC
- CD
- DE
Fazendo isso teremos que:
Como essa fórmula independe do comprimento, podemos calcular uma das equações e depois substituir na estrutura respeitando o sinal.
Substituindo na estrutura teremos que:
Para as barras CF e DG, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essas barras do tipo engastadas e apoiadas, e a fórmula a ser usada nela é:
E aplicando isso a nossa estrutura teremos que:
Perceba que para respeitar a regrinha de o momento sempre sair das fibras inferiores e ir pra superiores, nós invertemos o sentido do momento para ficar tudo certinho.
Substituindo na fórmula teremos que
Olhando a estrutura com todos os momentos teremos que:
Assim teremos que a rigidez total em D será dado por:
Passo 3
Agora vamos rotacionar a chapa 1, para podermos determinar os valores de , e .
Perceba que as duas barras que chegam na chapa 1 são Bi-engastadas, logo a fórmula a ser usada é:
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Passo 4
Agora vamos rotacionar a chapa 2, para podermos determinar os valores de , e .
Perceba que as duas barras horizontais que chegam na chapa 2 são Bi-engastadas, e a barra vertical que chega na chapa 2 é engastada e apoiada, logo as fórmulas a serem usadas são:
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Passo 5
Agora vamos rotacionar a chapa 3, para podermos determinar os valores de , e .
Perceba que a barra horizontal que chega na chapa 3 é Bi-engastadas, e a barra vertical que chega na chapa 3 é engastada e apoiada, logo as fórmulas a serem usadas são:
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Passo 6
Organizando o sistema temos que:
Substituindo temos que:
Assim o nosso sistema será:
E perceba que como não usamos fator de redução, os valores de deltas já nós darão as rotações diretas dos pontos pedidos, sendo assim teremos que: