Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Usando o método de williot para temperatura

Ver Todos os Exercícios

Teoria

Introdução

Na ultima aula aprendemos apenas a montar o nosso williot de temperatura a partir da seguinte estrutura:

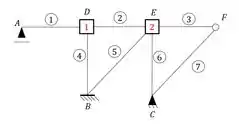
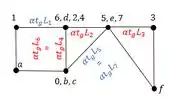
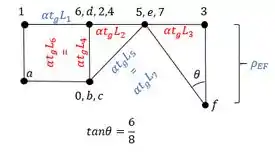
E obtemos o williot completo dado pela figura abaixo, em que as medidas determinadas por calculo são dadas também:

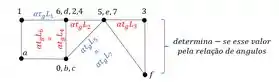
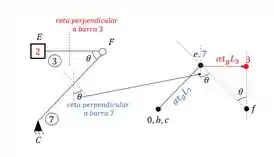
Mas como podemos usar isso para determinar as rigidezes da nossa barra? É isso que vamos fazer nessa aula.

Determinação do nome das barras

Nesse caso basta seguirmos o mesmo principio que aprendemos no método de williot para recalque, sempre nomeamos a barra na ordem que fomos descobrindo os pontos, ou seja, se fizermos em ordem o nome de cada ponto que determinamos, teremos que:

b , c , e ,   f ,   d ,   a

Ou seja, seguindo essa ordem, o nome de cada barra, será:

b a r r a   D A

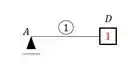
pois determinamos o D antes do A, e repetindo a sequencia em todas teremos que:

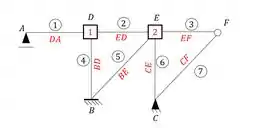
Determinação do deslocamento das barras

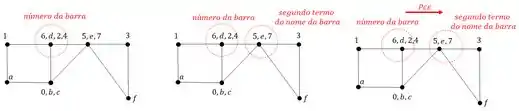
Perceba que agora as nossas barras tem um nome e um número, por exemplo a barra 1 que se chama DA. Porque isso é importante? Porque se quisermos saber o deslocamento da barra DA usando williot, precisamos primeiro procurar no Williot o número da barra, no nosso caso a barra 1:

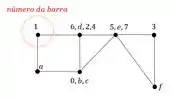
E em seguida determinamos o segundo termo do nome da nossa barra, ou seja, se a Barra é DA, então determinamos o ponto A.

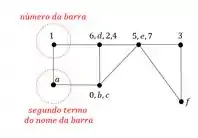
E o deslocamento da barra DA será dado do número da barra para o segundo termo do seu nome, sendo assim o deslocamento será dado por:

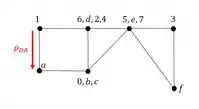
E onde aplicamos ele? Aplicamos também no ponto que simboliza o segundo termo do nome da barra. Ou seja, no osso caso aplicaremos no ponto A. tendo isso basta usarmos as equações para determinação das rigidezes, fazendo isso para o resto das barras teremos que:

ED (barra 2)

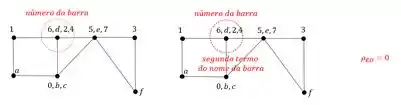
EF (barra 3)

Aplicado no ponto F.

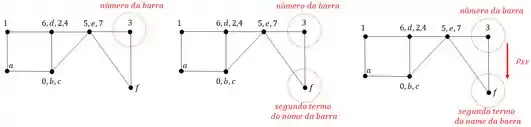
BD (barra 4)

BE (barra 5)

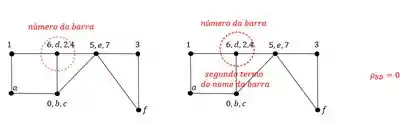
CE (barra 6)

Aplicado no ponto E.

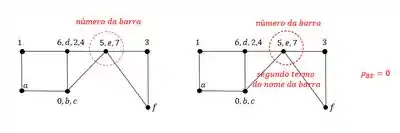
CF (barra 7)

Aplicado no ponto F. Porém perceba que a barra CE é rotulada tanto no ponto C quanto no ponto F, ou seja, independente do deslocamento que se tenha, os momentos serão zero devido as rótulas, o que significa que as rigidezes nesse caso também serão zero. Com isso agora só basta separarmos as barras com deslocamento, agindo no ponto que definimos e determinarmos as suas rigidezes, sendo assim teremos que:

Determinação das rigidezes

Sabemos que para cada barra os deslocamentos serão:

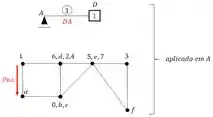
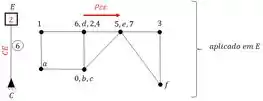
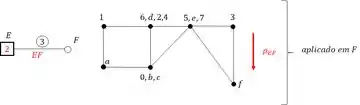
E temos um último aplicado em F, mas que podemos rejeitar porque lembre-se que ambas as bordas (extremidades) eram rotuladas, ou seja, não produzira rigidezes que nos interessem. Como se trata de um deslocamento, podemos usar as seguintes equações para determinação das rigidezes:

Começando pela barra DA, temos que:

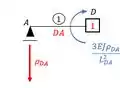
Para determinar ρ D A precisamos usar as relações que achamos no williot dadas pelas fórmulas α T g L , que encontramos aqui embaixo:

Outra parada importante que vale notar é que ele age na nossa chapa 1, logo teremos, lembrando que o sentido horário é negativo:

β 10 = - 3 E J ρ D A L D A 2

Então se soubéssemos que:

E J α = 1   k N m / ° C

L 1 = L 2 = L 3 = 8 m

L 6 = L 4 = 6 m

T g = 20   ° C

Perceba que pelo williot ali de cima, o valor de ρ D A é a distância entre o ponto 1 e “a”, que pelo williot vemos que vale

ρ D A = α T g L 6 = α T g L 4 = α .   20   . 6 = 120 α

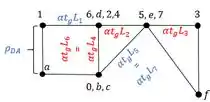
Substituindo teremos que:

β 10 = - 3 E J ρ D A L D A 2 = - 3 E J 120 α L D A 2 = - 3   .     1     .     120 8 2 = - 5,6

E agora indo para a barra CE, temos que:

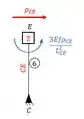
Para determinar ρ C E precisamos usar as relações que achamos no williot dadas pelas fórmulas α T g L , que encontramos aqui embaixo:

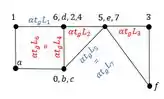
Outra parada importante que vale notar é que ele age na nossa chapa 2, logo teremos, lembrando que o sentido anti-horário é positivo:

β 20 = 3 E J ρ C E L C E 2

Então se soubéssemos que:

E J α = 1   k N m / ° C

L 1 = L 2 = L 3 = 8 m

L 6 = L 4 = 6 m

T g = 20   ° C

Perceba que pelo williot ali de cima, o valor de ρ C E é a distância entre o ponto 2 e “e”, que pelo williot vemos que vale

ρ C E = α T g L 2 = α .   20   . 8 = 160 α

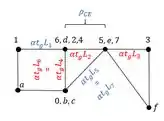
Substituindo teremos que:

β 20 = 3 E J ρ C E L C E 2 = 3 E J 160 α L C E 2 = 3   .     1     .     160 6 2 = 13,3

E por fim a barra EF, temos que:

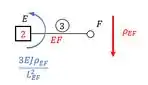
Para determinar ρ E F precisamos usar as relações que achamos no williot dadas pelas fórmulas α T g L , que encontramos aqui embaixo:

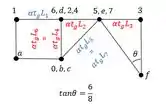
Outra parada importante que vale notar é que ele age na nossa chapa 2, logo teremos, lembrando que o sentido anti-horário é positivo:

β 20 = 3 E J ρ E F L E F 2

Então se soubéssemos que:

E J α = 1   k N m / ° C

L 1 = L 2 = L 3 = 8 m

L 6 = L 4 = 6 m

T g = 20   ° C

Perceba que pelo williot ali de cima, o valor de ρ E F é a distância entre o ponto 3 e “f”, que pelo williot vemos que vale

t a n θ = α T g L 3 ρ E F = 6 8

ρ E F = 8 α T g L 3 6 = 8 6   .   20   .   8   .   α = 213 α

Substituindo teremos que:

β 20 = 3 E J ρ E F L E F 2 = 3 E J 213 α L E F 2 = 3   .     1     .     213 8 2 = 10

E como temos dois caras agindo na chapa 2, basta somarmos eles dois para termos o resultante:

β 20 = 13,3 + 10 = 23,3

E para determinação de β 11 ,   β 22 ,   β 12 … basta que façamos o que estamos cansados de conhecer, que é basicamente rotacionar as nossas chapas e analisar o comportamento na estrutura, e assim conseguimos resolver toda e qualquer estrutura usando o williot para variação de temperatura na nossa estrutura.

Bora fazer exercício pra ficar craque nisso.

Determinação do deslocamento das barras

ED (barra 2)

EF (barra 3)

BD (barra 4)

BE (barra 5)

CE (barra 6)

CF (barra 7)

Determinação das rigidezes

Exercícios Resolvidos

Exercício Resolvido #1

Origem do Exercício

Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante ( ∆ t = 0 ), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico α os comprimentos dados abaixo e para a temperatura do centro de gravidade use T g . Determine também os deslocamentos e os pontos em que agem.

Passo 1

Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas segui o nosso passo a passo.

Primeiro precisamos determinar os nossos indeslocáveis.

Isso é bem simples, sabemos que no nosso caso os dois indeslocáveis, que vão se unir a nossa origem são os pontos A e C, dessa maneira teremos que:

Passo 2

Em seguida devemos determinar o ponto que tenha em comum os pontos a e C, que no nosso caso é o ponto B. sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 1 = α T g l 1 e ∆ 2 = α T g l 2 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.

Passo 3

Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 4

Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.

Primeiro sabemos que a ordem de determinação dos pontos foi:

a , c , b

  • Barra 1

    • Sabendo a ordem podemos definir que o nome da barra 1 é AB. Achando o ponto 1 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra AB. Sendo assim teremos que:

  • Barra 2

    • Sabendo a ordem podemos definir que o nome da barra 2 é CB. Achando o ponto 2 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é CB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra CB. Sendo assim teremos que:

    Resposta

    Williot

    Deformações e ponto de aplicação:

  • Barra 1

  • Barra 2

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

Origem do Exercício

Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante ( ∆ t = 0 ), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico α os comprimentos dados abaixo e para a temperatura do centro de gravidade use T g . Determine também os deslocamentos e os pontos em que agem.

Passo 1

Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas seguir o nosso passo a passo.

Primeiro precisamos determinar os nossos indeslocáveis.

Isso é bem simples, sabemos que no nosso caso os três indeslocáveis, que vão se unir a nossa origem são os pontos A, E e D, dessa maneira teremos que:

Passo 2

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto C, que tem em comum os pontos E e D.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em C, e só depois descobrimos de fato o ponto C.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 4 = α T g l 4 e ∆ 3 = α T g l 3 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto C.

Tendo os pontos que representam as barras que chegam no ponto C, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto C. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 3

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto B, que tem em comum os pontos C e A.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 1 = α T g l 1 e ∆ 2 = α T g l 2 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.

Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 4

Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.

Primeiro sabemos que a ordem de determinação dos pontos foi:

a , e ,   d ,   c ,   b

  • Barra 1

    • Sabendo a ordem podemos definir que o nome da barra 1 é AB. Achando o ponto 1 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra AB. Sendo assim teremos que:

  • Barra 2

    • Sabendo a ordem podemos definir que o nome da barra 2 é CB. Achando o ponto 2 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é CB, o segundo termo será o B. Sendo assim teremos que:

    Como o ponto 2 e o ponto B estão na mesma posição, a deformação relativa entre eles é zero, sendo assim teremos que:

  • Barra 3

    • Sabendo a ordem podemos definir que o nome da barra 3 é EC. Achando o ponto 3 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é EC, o segundo termo será o C. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto C da barra EC. Sendo assim teremos que:

  • Barra 4

    • Sabendo a ordem podemos definir que o nome da barra 4 é DC. Achando o ponto 4 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é DC, o segundo termo será o C. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto C da barra DC. Sendo assim teremos que:

    Resposta

    Williot

    Deformações e ponto de aplicação:

  • Barra 1

  • Barra 2

  • Barra 3

  • Barra 4

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Origem do Exercício

Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante ( ∆ t = 0 ), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico α os comprimentos dados abaixo e para a temperatura do centro de gravidade use T g . Determine também os deslocamentos e os pontos em que agem.

Passo 1

Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas seguir o nosso passo a passo.

Primeiro precisamos determinar os nossos indeslocáveis.

Isso é bem simples, sabemos que no nosso caso os três indeslocáveis, que vão se unir a nossa origem são os pontos A, E e D, dessa maneira teremos que:

Passo 2

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto B, que tem em comum os pontos A e D.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 1 = α T g l 1 e ∆ 2 = α T g l 2 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.

Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 3

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto C, que tem em comum os pontos B e E.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em C, e só depois descobrimos de fato o ponto C.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 3 = α T g l 3 e ∆ 4 = α T g l 4 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto C.

Tendo os pontos que representam as barras que chegam no ponto C, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto C. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 4

Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.

Primeiro sabemos que a ordem de determinação dos pontos foi:

a , d ,   e ,   b ,   c

  • Barra 1

    • Sabendo a ordem podemos definir que o nome da barra 1 é AB. Achando o ponto 1 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:

    Como o ponto 1 e B estão na mesma posição, teremos que:

  • Barra 2

    • Sabendo a ordem podemos definir que o nome da barra 2 é DB. Achando o ponto 2 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é DB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra DB. Sendo assim teremos que:

  • Barra 3

    • Sabendo a ordem podemos definir que o nome da barra 3 é BC. Achando o ponto 3 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é BC, o segundo termo será o C. Sendo assim teremos que:

    Como os pontos 3 e C estão na mesma posição, teremos que.

  • Barra 4

    • Sabendo a ordem podemos definir que o nome da barra 4 é EC. Achando o ponto 4 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é EC, o segundo termo será o C. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto C da barra DC. Sendo assim teremos que:

    Resposta

    Williot

    Deformações e ponto de aplicação:

  • Barra 1

  • Barra 2

  • Barra 3

  • Barra 4

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Origem do Exercício

Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante ( ∆ t = 0 ), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico α os comprimentos dados abaixo e para a temperatura do centro de gravidade use T g . Determine também os deslocamentos e os pontos em que agem.

Passo 1

Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas seguir o nosso passo a passo.

Primeiro precisamos determinar os nossos indeslocáveis.

Isso é bem simples, sabemos que no nosso caso os três indeslocáveis, que vão se unir a nossa origem são os pontos A, E e D, dessa maneira teremos que:

Passo 2

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto C, que tem em comum os pontos E e D.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em C, e só depois descobrimos de fato o ponto C.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 1 = α T g l 1 e ∆ 2 = α T g l 2 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto C.

Tendo os pontos que representam as barras que chegam no ponto C, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto C. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 3

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto B, que tem em comum os pontos A e C.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 3 = α T g l 3 e ∆ 4 = α T g l 4 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.

Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 4

Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.

Primeiro sabemos que a ordem de determinação dos pontos foi:

a , d ,   e ,   c ,   b

  • Barra 1

    • Sabendo a ordem podemos definir que o nome da barra 1 é EC. Achando o ponto 1 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é EC, o segundo termo será o C. Sendo assim teremos que:

    Sabemos que a deformação ocorre também no segundo termo do nome, ou seja, se a barra é EC, aplicaremos a deformação em C, sendo assim teremos que:

  • Barra 2

    • Sabendo a ordem podemos definir que o nome da barra 2 é DC. Achando o ponto 2 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é DC, o segundo termo será o C. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto C da barra DC. Sendo assim teremos que:

  • Barra 3

    • Sabendo a ordem podemos definir que o nome da barra 3 é CB. Achando o ponto 3 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é CB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra CB. Sendo assim teremos que:

  • Barra 4

    • Sabendo a ordem podemos definir que o nome da barra 4 é AB. Achando o ponto 4 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra AB. Sendo assim teremos que:

    Resposta

    Williot

    Deformações e ponto de aplicação:

  • Barra 1

  • Barra 2

  • Barra 3

  • Barra 4

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Origem do Exercício

Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante ( ∆ t = 0 ), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico α os comprimentos dados abaixo e para a temperatura do centro de gravidade use T g . Determine também os deslocamentos e os pontos em que agem.

Passo 1

Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas seguir o nosso passo a passo.

Primeiro precisamos determinar os nossos indeslocáveis.

Isso é bem simples, sabemos que no nosso caso os três indeslocáveis, que vão se unir a nossa origem são os pontos A e C dessa maneira teremos que:

Passo 2

Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto B, que tem em comum os pontos A e C.

Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.

Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação ∆ 1 = α T g l 1 e ∆ 2 = α T g l 2 . Fazendo isso teremos que:

Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.

Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:

Ligando os pontos teremos que:

Passo 3

Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.

Primeiro sabemos que a ordem de determinação dos pontos foi:

a , d ,   b

  • Barra 1

    • Sabendo a ordem podemos definir que o nome da barra 1 é AB. Achando o ponto 1 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:

    Sabemos que a deformação ocorre também no segundo termo do nome, ou seja, se a barra é AB, aplicaremos a deformação em B, sendo assim teremos que:

  • Barra 2

    • Sabendo a ordem podemos definir que o nome da barra 2 é CB. Achando o ponto 2 no nosso williot teremos que.

    E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é CB, o segundo termo será o B. Sendo assim teremos que:

    E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra CB. Sendo assim teremos que:

    Resposta

    Williot

    Deformações e ponto de aplicação:

  • Barra 1

  • Barra 2

Resposta

Ei, a resposta está no passo a passo :)