Teoria
Você sabe o que é flambagem?
A flambagem é o encurvamento que acontece em peças esbeltas devido a compressão axial.
Se liga na imagem abaixo que vai ficar mais claro:
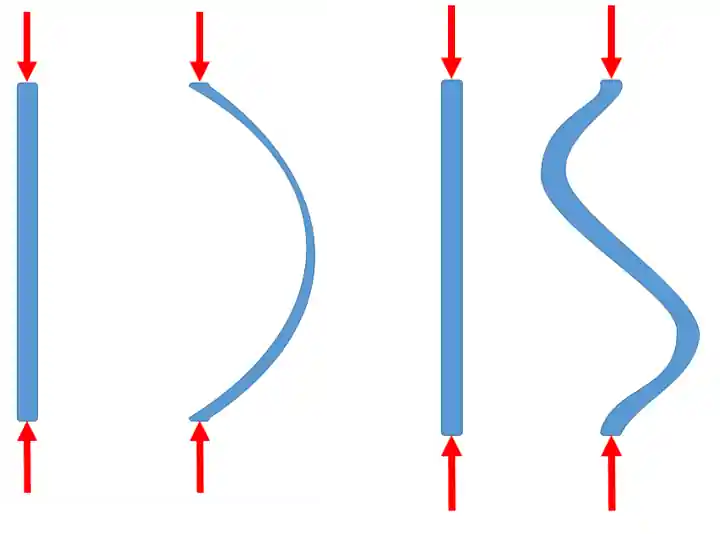
Vocês concordam comigo que quanto mais fina for essa coluna mais difícil será de se equilibrar?
A maior parte do estudo da flambagem recai no conceito de colunas, porque são estruturas que podem se tornar extremamente instáveis devido a dois fatores: compressão e esbelteza. Então, se uma compressão muito grande for aplicada sobre uma coluna esbelta (esbelta significa fina, beleza?) pode ocorrer o fenômeno da flambagem.
Se liga nesse vídeo sobre Flambagem que o Responde Aí preparou especialmente pra você 🧡
Mas não acabou! Me segue que tem mais 👇
Uma coisa muito importante pra gente ter em mente é que a estrutura não pode sofrer flambagem, ok?! É exatamente para isso que vamos fazer a análise de estabilidade, para evitar esse tipo de defeito.
Na vida real sempre ocorrerá uma ligeira deflexão, o que não pode acontecer é que essa deflexão supere um valor limite. Esse valor limite da deflexão acontece quando uma carga crítica é imposta na coluna. Ou seja, antes da carga crítica a coluna sofre uma deflexão desprezível e após essa carga crítica a deflexão se torna um problema, ocorre a flambagem.
Equilíbrio Estável e Instável
Um equilíbrio estável é aquele que mesmo sofrendo uma mudança em seu formato retorna para a posição original. Já o equilíbrio instável não retorna para a posição original.
Para entendermos melhor a diferença entre equilíbrio estável e equilíbrio instável vamos observar o limite entre um e outro. Se liga na imagem abaixo:
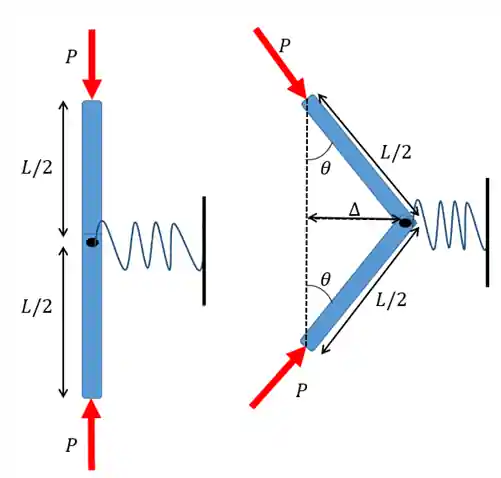
O desenho acima traz duas barras conectadas entre si e com uma mola de constante
Nesse quadro resumo abaixo, podemos ver como calculamos a caga crítica e diferenciamos o equilíbrio estável do instável. 👇

Beleza, mas vamos entender melhor como calcular essa tal de carga crítica, afinal nos problemas reais, na maioria das vezes, não vamos ter uma mola!
Carga Crítica: Fórmula
Podemos calcular a carga crítica usando a seguinte fórmula:
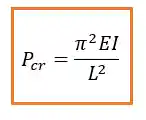
Onde:
é o comprimento; é o coeficiente de elasticidade; é o momento de inércia.
Tensão Crítica
Já que temos uma carga crítica gente pode definir uma tensão crítica também. Para isso usamos a seguinte fórmula:
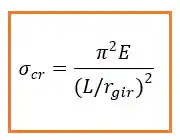
Onde:
é o comprimento; é o coeficiente de elasticidade; é o raio de giração.
Agora que você já tá sabendo tudo sobre flambagem, confere esses exercícios resolvidos aqui em baixo! 👇
Equilíbrio Estável e Instável
Carga Crítica: Fórmula
Tensão Crítica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Qual a diferença entre flambagem e flexão?
Passo 1
A flexão é um fenômeno de deformação da viga e ocorre sempre no sentido das forças. lembre-se que a flexão depende muito do momento fletor e pode ser calculada como:
Se existe momento fletor então existirá flexão.
Já a flambagem é defeito estrutural associado à instabilidade da estrutura. A flambagem pode ou não ocorrer numa estrutura sujeito à uma carregamento com momentos fletores, mas depende fundamentalmente das tensões de compressão.
Passo 2
Enquanto a flexão é a deformação devido à uma carga. A flambagem é um defeito estrutural associado à instabilidade da estrutura.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
A análise de estabilidade está intimamente relacionada com o conceito de flambagem, pois dependendo da esbeltez de uma coluna ela pode se tornar instável e ocorrer o defeito denominado flambagem. Porém, ao projetar uma coluna, que outro fator também é muito importante a ser analisado para que a coluna possa ser corretamente dimensionada?
Passo 1
Como o enunciado já diz, a análise de estabilidade é muitíssimo importante para saber se uma coluna irá sofrer flambagem.
Porém, é importante lembrar que a flambagem ocorre principalmente em barras esbeltaz, ou seja, possuem um comprimente elevado quando comparado com sua área.

Imagine agora que temos uma coluna com uma altura pequena, mas com uma área muito grande. Essa coluna dificilmente irá sofrer flambagem mas pode sofrer devido ao escoamente por compressão.
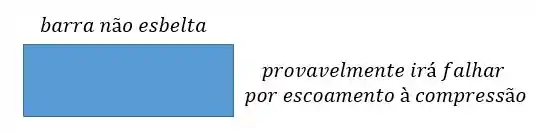
Passo 2
O limite de escoamento à compressão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 486. Problema 13.2
A coluna é composta por um elemente estrutural rígido preso por um pino na base e acoplado a uma mola no topo. Se a mola não estiver esticada quando a coluna estiver em posição vertical, determine a carga crítica que pode ser aplicada à coluna.
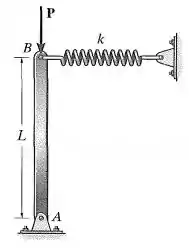
Passo 1
O problema pede a carga crítica que pode ser aplicada à coluna, ou seja, a maior carga que pode ser aplicada à coluna sem que haja alteração no equilíbrio.
Desta forma, a gente tem que fazer um diagrama das forças e achar uma relação entre a força da mola e a carga .
Lembre-se também que iremos considerar ângulos pequenos porque se a angulação for muito grande vamos ter uma situação de equilíbrio não-estável, que não queremos.
Passo 2
Vamos começar fazendo o diagrama de corpo livre dessa barra, considerando uma pequena deformação:
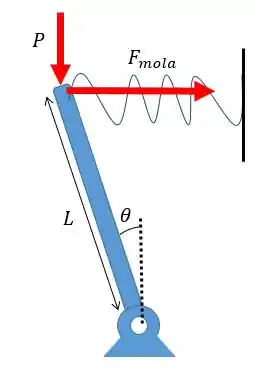
A partir desse diagrama a gente pode aplicar o somatório dos momentos no pino e igualar a zero para obter a condição de equilíbrio:
A deformação da mola é dada por , logo:
Simplificando:
Como o nosso ângulo é muito pequeno podemos fazer a aproximação
Logo,
Passo 3
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
A barra rígida representanda abaixo sofre um carregamento vertical. Encontre o valor da carga crítica, sabendo que a costante da mola torcional vale
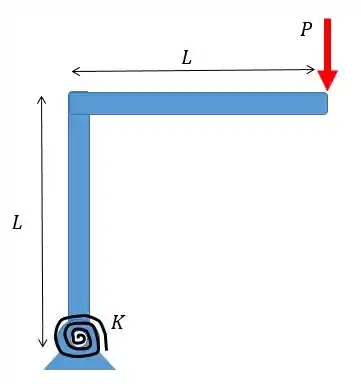
Passo 1
Vamos lá, galera. Esse problema pede o carregamento máximo ou seja ele quer . Para achar a gente precisa considerar duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Portanto a primeira coisa que devemos fazer é um diagrama das foças. Partiu?
Passo 2
Aqui a gente nem precisa fazer um diagrama de forças muito elaborado, apeas precisamos colocar o momento que a mola torcional exerce.
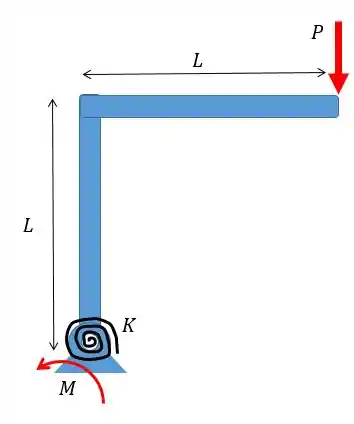
Como a gente não sabe o valor da força que atua no pino. Nós vamos aplicar o somatório de momentos nesse ponto:
Sabendo que o momento da mola contrapõe o momento da carga vamos ter:
Portanto a carga crítica desse sistema vai ser:
Resposta
Exercício Resolvido #5
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 1096. Exercício 11 - 2
Sabendo-se que a mola torcional em é de constante e que a barra é rígida, determinar a carga crítica .
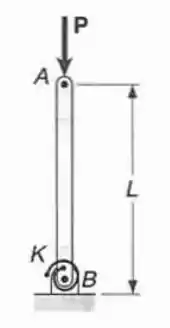
Passo 1
A carga crítica, pedida no problema, é a maior carga que mantenha o sistema numa equilíbrio estável. Ou seja, temos de pensar sempre em duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Passo 2
Para aplicar as equações de equilíbrio vamos fazer um diagrama de forças, já considerando uma pequena angulação.
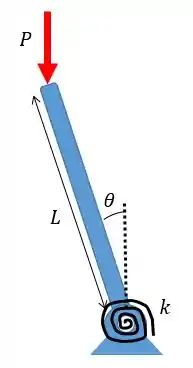
Agora vamos aplicar o somatório de momentos em relação ao pino, lembrando que o sistema está em equilíbrio, logo, esta soma deve ser igual a zero.
Desta forma vamos ter que o momento da carga será igual ao momento da mola de torção:
Fazendo a aproximação para ângulos pequenos podemos obter:
Resposta
Exercício Resolvido #6
Elaboração própria
A barra rígida representanda abaixo sofre um carregamento vertical. Calcule o valor máximo de para que a barra se mantenha estável, sabendo que ambas as molas lineares tem coeficiente e a mola torcional tem coeficiente .
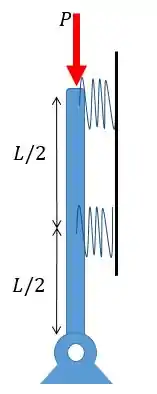
Passo 1
Vamos lá, galera. Esse problema pede o carregamento máximo ou seja ele quer . Para achar a gente precisa considerar duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Portanto a primeira coisa que devemos fazer é um diagrama das foças. Partiu?
Passo 2
Fazendo o diagrama das forças considerando uma pequena deflexão vamos ter:
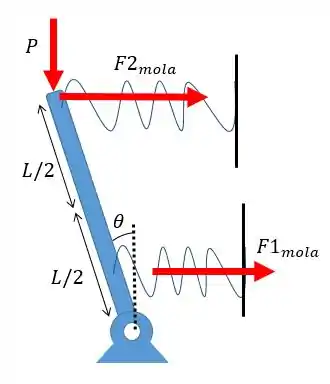
Agora fica mais fácil de comparar essas forças, correto?
Como a gente não sabe o valor da força que atua no pino. Nós vamos aplicar o somatório de momentos nesse ponto:
Como o momento da carga contrapõe os momentos das molas vamos ter:
Vamos calcular a força das molas no próximo passo.
Passo 3
A força de cada mola será dada por:
Substituindo na equação vamos obter:
Simplificando pelo termo vamos ter:
Como a variação angular é pequena para mantermos o equilíbrio estável a gente pode considerar , logo:
Resposta
Exercício Resolvido #7
Elaboração própria
A barra rígida representanda abaixo sofre um carregamento vertical. Calcule o valor máximo de para que a barra se mantenha estável, sabendo que ambas as molas lineares tem coeficiente e a mola torcional tem coeficiente .
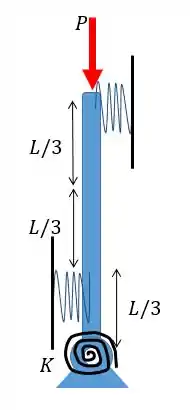
Passo 1
Vamos lá, galera. Esse problema pede o carregamento máximo ou seja ele quer . Para achar a gente precisa considerar duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Portanto a primeira coisa que devemos fazer é um diagrama das foças. Partiu?
Passo 2
Fazendo o diagrama das forças considerando uma pequena deflexão vamos ter:
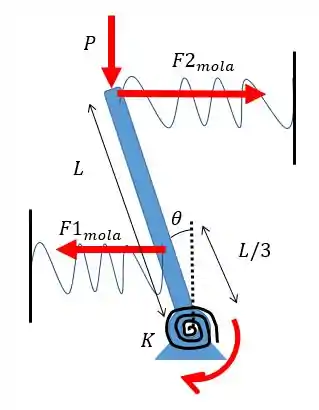
Agora fica mais fácil de comparar essas forças, correto?
Como a gente não sabe o valor da força que atua no pino. Nós vamos aplicar o somatório de momentos nesse ponto:
Agora vamos ter que os momentos e agem no sentido contrário aos de e da mola torcional, portanto:
obs: O momento de uma mola torcional é dado por
Vamos calcular a força das molas no próximo passo.
Passo 3
A força de cada mola será dada por:
Substituindo na equação vamos obter:
Lembrando que podemos fazer a aproximação porque o ângulo é pequeno. Assim vamos ter:
Simplificando pelo termo vamos ter:
Como a variação angular é pequena para mantermos o equilíbrio estável a gente pode considerar , logo:
Resposta
Exercício Resolvido #8
1ª Lista de exercícios – Resistência dos Materiais II – Prof. Dornelles. Ex 11-3
Duas barras rígidas e são conectadas a uma mola de constante , como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica para o sistema.
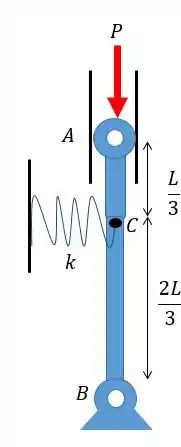
Passo 1
Vamos resolver mais um problema aqui sobre carga crítica num sistema com mola. Para começar é importante fazer um esquema de como fica o nosso sistema com uma pequena angulação:
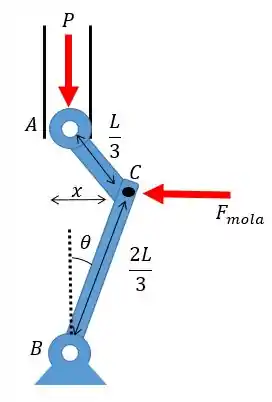
Aí, pessoal, a partir disso a gente tem que aplicar nossas equações de equilíbrio estático e lembrar de fazer as aproximações:
Já que se trata de um ângulo bem pequeno.
Passo 2
Ao olhar o nosso diagrama podemos ver que é a própria deformação da mola. Podemos calcular o valor de por meio dos dois triângulos formados:
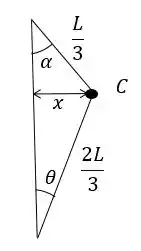
Podemos calcular de duas formas:
Fazendo a aproximação:
Vamos ter:
Logo,
Passo 3
Agora que sabemos os dois ângulos nós podemos voltar ao nosso diagrama e analisar apenas a barra :
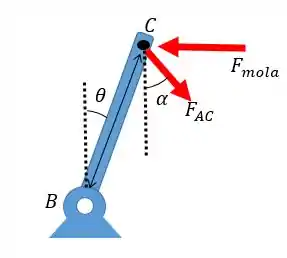
Onde a força é a força que a barra faz na barra , como essa força depende verticalmente apenas da força nós vamos ter:
Logo,
Fazendo o somatório dos momentos em nós vamos ter:
Aplicando as aproximações dos ângulos e nós vamos ter:
Como
E a equação da mola é:
Onde:
Logo,