Carga crítica
Produzido por Pablo RicardoTeoria
Faaala, galerinha!! No tópico passado a gente abordou o conteúdo relativo à carga crítica e dessa vez vamos aprofundar mais nesse assunto. Antes a gente tinha visto vários exemplos de estruturas com molas e achamos uma tabela para a carga crítica. Ambos estão aqui embaixo:
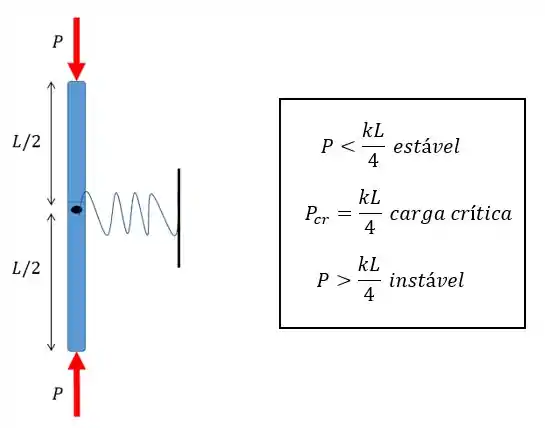
Mas e se não tiver uma mola no nosso sistema eu ainda posso falar de estabilidade e flambagem?
É claro que sim. Na verdade na maior parte das vezes não vai haver mola mesmo. Agora vamos aprender a resolver problemas de flambagem de estruturas “normais” sem a tal da mola.
Linha elástica aplicada à flambagem
Pessoal, o estuda da linha elástica é muito importante quando a gente fala de flambagem. Isso porque a flambagem é trata da deflexão de uma coluna por causa da instabilidade e a linha elástica é a linha que define essa deflexão. Tudo a ver né?
Caso você tenha esquecido, a equação da linha elástica é a seguinte:
Onde é a deflexão, o momento fletor, o coeficiente de elasticidade do material e o momento de inércia.
A partir dessa equação a gente vai chegar num novo conceito de carga crítica que vai englobar os aspectos da nossa coluna como o módulo de elasticidade e o momento de inércia .
Vamos considerar uma coluna, com as extremidades livres para girar, sujeita a compressão por uma força e ao lado vamos mostrar também um corte nessa coluna afim de conhecer o momento fletor .
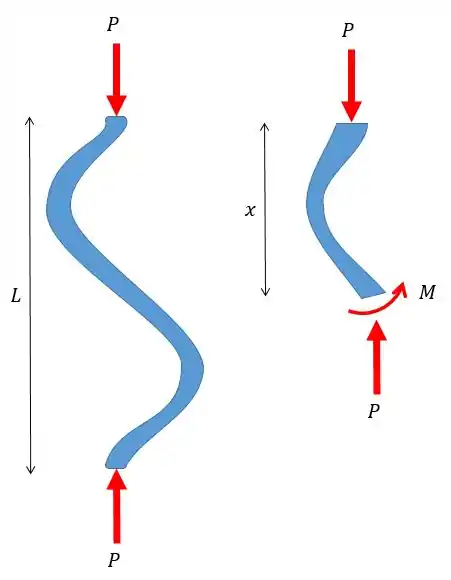
O momento fletor pode ser achado como a força vezes a deflexão no ponto .
Com isso vamos poder substituir esse momento na nossa equação da linha elástica:
Bom, aqui o nosso objetivo não é resolver equações diferenciais então já vou trazer para você o resultado disso aí:
Esse é o número de “barrigas” da nossa barra flambada. Mas aqui é importante perceber que a gente quer achar a carga crítica, correto? Essa carga vai ser a menor possível, logo vamos substituir (sempre vamos usar para calcular a carga crítica) e obter:
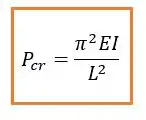
Onde:
- é o comprimento
- o coeficiente de elasticidade
- que é o momento de inércia.
Pessoal, a gente tem que lembrar que esse resultado é para uma coluna com as extremidades livres para girar, ou seja, apoiada em pinos, por exemplo.
Uhulll!! Achamos então uma equação para achar a carga crítica atuando numa coluna a partir de grandezas intrínsecas à própria coluna e a um tipo específico de apoio.
Tensão crítica
Já que temos uma carga crítica gente pode definir uma tensão crítica também. É só lembrar que a tensão é a carga sobre a área:
Substituindo na equação vamos obter:
Agora a gente ainda pode utilizar mais um macete! O momento de inércia pode ser dado como a área vezes o raio de giração ao quadrado, lembram disso?
Sendo assim a gente pode substituir na equação e obter:
Simplificando o termo da área:
Essa equação muitas vezes é escrita da forma:
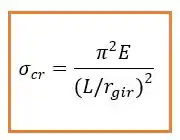
Mas não faz diferença nenhuma! É a mesma coisa só com uma carinha diferente. O legal é que o termo é definido como índice de esbeltez.
Eixo de flambagem
Pra terminar esse conteúdo bacana a gente só precisa saber de mais uma coisinha. A flambagem sempre vai ocorrer no eixo que tem o menor momento de inércia. Por isso não é lá muito inteligente fazer uma coluna retangular por exemplo. Colunas com perfis quadrados e circulares resistem melhor à flambagem.
Por exemplo, a nossa coluna representada abaixo irá fletir entorno do eixo , que possui o menor momento de inércia.
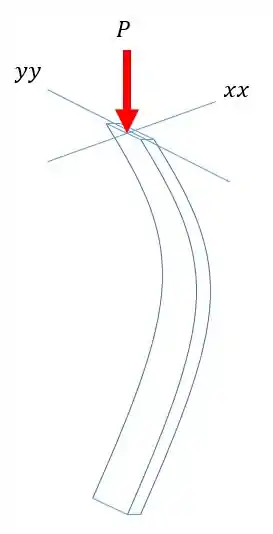
Ficamos por aqui e que tal fazer uns exercícios pra amaciar o nosso cerebelo?
Tensão crítica
Eixo de flambagem
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
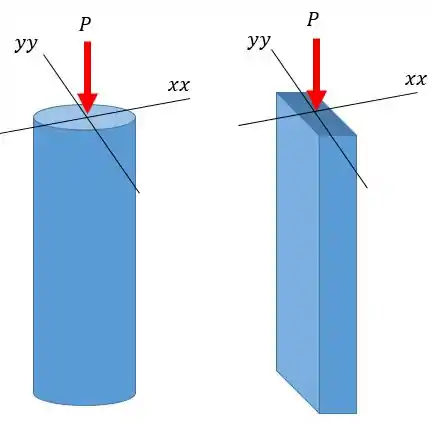
Uma engenheira deve projetar uma coluna para suportar uma carga total . Sabendo que o projeto admite apenas dois tipos de colunas do mesmo material, área e comprimento mas uma retangular e outra circular. Qual coluna a projetista deve utilizar se estiver interessado exclusivamente na maior estabilidade possível?
Passo 1
Faaala aí pessoal!! Vamos começar bem de leve e entender o que esse problema quer. A nossa amiga engenheira está interessada na estabilidade, logo a gente está olhando para as equações de flambagem.
Lembre-se também que a flambagem não pode ocorrer!! Isso seria um problema estrutural de instabilidade.
A nossa coleguinha tem duas opções e queremos a que fornece a maior estabilidade:

E aí, qual você escolheria para se equilibrar em cima? É basicamente essa a questão!
Passo 2
Para responder essa questão da maneira mais correta possível a gente tem que lembrar da equação da flambagem com relação à carga crítica:
O problema nos fala que as colunas tem o mesmo comprimento e são feitas do mesmo material logo e são irrelevantes na análise deste problema, também é.
Logo a carga crítica vai ser proporcional ao momento de inércia da coluna
Ou seja, devemos escolher aquela que nos fornece o maior momento de inércia porque assim a coluna consegue suportar uma carga crítica maior.
Passo 3
Vamos olhar novamente as nossas colunas, agora com dois eixos apontados:
Não acho que seja necessário ficar calculando o momento de inércia de cada eixo, mas para refrescar sua memória o momento de inércia é calculado como:
Pessoal, pouco me interessam esses valores, sabe por quê? Como ambas tem a mesma área então o momento de inércia de um dos eixos da coluna retangular vai ser maior do que o do círculo e o outro menor. Podemos escrever como:
Correto? O momento de inércia do círculo é igual em qualquer direção, só pra lembrar.
Agora a gente só precisa lembrar que a flambagem é uma danada e sempre vai ocorrer em torno do menor momento de inércia.
Sendo assim, não interessa que a coluna retangular tem um eixo com o momento de inércia maior, porque vamos analisar sempre o menor momento de inércia.
Logo, a coluna circular é mais estável que a retangular =D
Colunas quadradas também são boas já que possuem o mesmo momento de inércia em ambas as direções. No quesito estabilidade, quanto mais homogênea for a distribuição dos momentos de inércia melhor!
Passo 4
A coluna circular é mais estável que a retangular.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Num projeto mecânico uma carga deve ser elevada por um pistão de aço no formato tubular com diâmetro externo de e espessura de . Sabendo que podemos considerar as extremidades desse pistão apoiadas por pinos calcule a máxima carga que esse pistão pode suportar sem sofrer flambagem. Dados: , comprimento do pistão .
Passo 1
Olá, pessoas!! Vamos resolver mais uma questãozinha de flambagem. Essa questão é bem direta e nos pede a máxima carga que o pistão pode suportar, aqui o pistão vai agir como se fosse uma coluna e queremos achar o .
Dessa forma vamos utilizar a equação:
Aí só precisamos calcular o momento de inércia e substituir na equação =)
Passo 2
Vamos calcular o momento de inércia então. Lembrando que para um círculo vamos ter:
Mas o pistão é um tubo vazado, então vamos ter o seguinte:
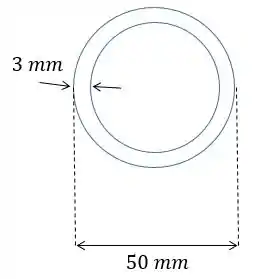
Assim,
Para achar o momento de inércia vamos fazer:
Substituindo os valores em metros vamos ter:
Passo 3
Agora é só substituir na equação
Passo 4
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Uma coluna retangular de área transversal e comprimento de é utilizada para suportar uma carga de . Sabendo que a coluna é feita de concreto com módulo de elasticidade de . Determine se a coluna irá sofrer flambagem. Dado: Considere apoios por pinos.
Passo 1
Oii, galera!! Mais uma questão aqui que pede basicamente a aplicação da fórmula de flambagem. Lembre-se que essa equação vale quando os apoios são livres para se mexer, como o problema fala de pinos então podemos utilizá-la.
A única coisa que a gente tem que prestar mais atenção é que devemos utilizar o menor momento de inércia da nossa coluna, beleza? Lembrem-se que a flambagem é uma danada e sempre vai acontecer no eixo do menor momento de inércia.
Passo 2
Vamos calcular o momento de inércia então. Lembrando que para um retângulo vamos ter:
Para achar o menor momento de inércia é só utilizar o menor termo no lugar do , já que esse termo é que vai ser elvado ao cubo:
Passo 3
Agora é só substituir na equação
Logo a nossa coluna suporta a carga de sem sofrer flambagem.
Passo 4
Logo a nossa coluna suporta a carga de sem sofrer flambagem.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Uma estrutura mecânica está apoiada com liberdade de giro sobre colunas de aço () com comprimento de . Sabendo que nessa coluna é utilizado o perfil de abas largas , qual o valor máximo da carga que pode ser aplicada sobre a coluna de modo a não haver falha nem por escoamento nem por instabilidade. Considere .
Passo 1
Meus amigos e minhas amigas, essa questão está falando sobre falha por escoamento e por instabilidade (flambagem). Logo vamos ter que fazer as duas análises para ter certeza que não vai dar ruim na nossa coluna.

Então vamos fazer primeiramente a análise de estabilidade e achar a carga crítica por meio da nossa equação da flambagem para colunas apoiadas em pinos (por causa da liberdade de giro):
depois vamos utilizar essa carga crítica para ver se não vai ocorrer escoamento:
Passo 2
Como o problema nos forneceu o perfil da barra a gente não precisa calcular o momento de inércia é só ir numa tabela de perfis de abas largas e achar . Aqui eu acho interessante você mesmo olhar numa tabelinha dessas para se acostumar com esse tipo de tabela, mas de qualquer forma vou fornecer os dados importantes aqui:
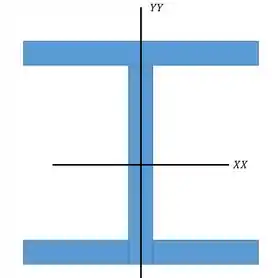
Gente, eu coloquei os dois momentos de inércia mas a gente só vai precisar de um, você lembra qual é?
O menor né!! Lembra que a flambagem é uma desgraçada e sempre vai atacar no pronto fraco da nossa coluna que é o menor momento de inércia. Dessa forma o momento de inércia que vamos utilizar é:
Passo 3
Agora é só substituir na equação da flambagem e achar a carga crítica:
Logo a máxima carga que a coluna consegue suportar sem sofrer flambagem é de .
Mas essa pode não ser a carga máxima porque essa coluna pode sofrer escoamento por compressão a uma carga de por exemplo...
Vamos conferir!
Passo 4
Para calcular a tensão de compressão vamos fazer:
Substituindo os valores vamos ter:
perceba que essa tensão é muito inferior à tensão de escoamento que é de .
Sendo assim a falha nessa estrutura ocorrerá primeiramente por flambagem. Isso talvez se explique pelo elevado comprimento da coluna (10 metros).
Passo 5
A maior carga admitida nessa configuração é de
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
Uma força de é aplicada ao sistema mecânica mostrado. Sabendo que todas as hastes são de aço . Determine se a coluna vertical sofrerá flambagem. Dado: As hastes possuem índice de esbeltez igual a e área igual a .
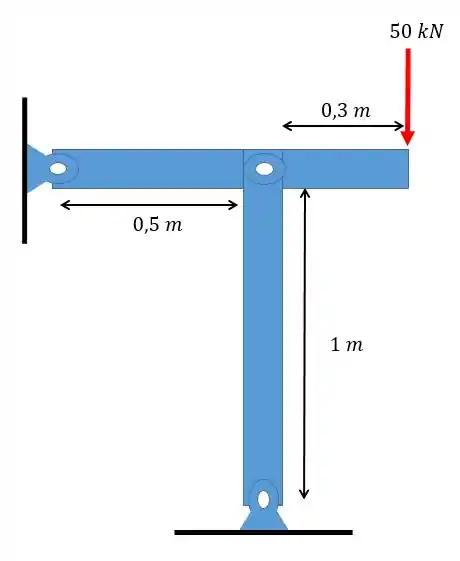
Passo 1
Pessoal, esse problema pede para calcularmos a tensão crítica de flambagem e nos deu o índice de esbeltez, vamos lembrar o que isso significa!
Índice de esbeltez é a relação entre o comprimento e o raio de giração da coluna
Isso é importante porque podemos calcular a tensão crítica a partir dessa grandeza, já que a tensão crítica pode ser calculada como:
Dessa forma, para resolver essa questão basta acharmos a tensão crítica a partir da equação da flambagem a cima e comparar com a tensão de compressão da nossa coluna.
Passo 2
Vamos calcular a tensão de compressão da coluna, para isso vamos fazer um diagrama de forças:
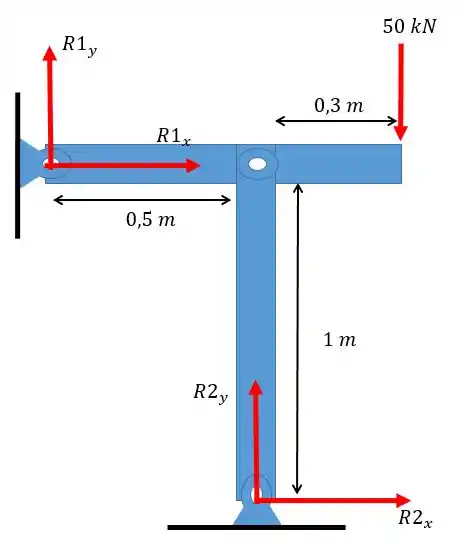
Agora percebam que as componentes horizontais não são importantes para o cálculo da flambagem da coluna vertical, por isso iremos queremos apenas dessa maneira podemos fazer aplicar o somatório dos momentos em torno da junção das hastes:
Pessoal, aqui é importante perceber que estamos olhando só para a barra horizontal, logo a força não entra nas nossas continhas.
Agora é só aplicar o somatório das forças em :
Passo 3
Para achar a tensão de compressão é só dividir pela área:
Vamos converter a área para metros:
Beleza, já temos a pressão a qual a nossa haste está submetida. Vamos achar agora a tensão crítica de flambagem
Passo 4
Agora é só substituir na equação da flambagem e achar a carga crítica:
Passo 5
Como a tensão de compressão é bem menor do que a tensão crítica de flambagem a nossa haste não sofrerá com a flambagem.
Passo 6
Como a tensão de compressão é bem menor do que a tensão crítica de flambagem a nossa haste não sofrerá com a flambagem.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.3
Uma coluna de aço tem comprimento de e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
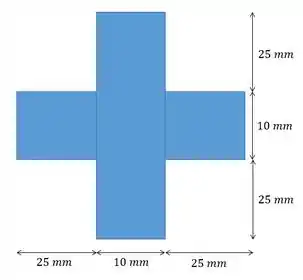
Passo 1
E aííí, meus queridos e minhas queridas, tudo belezinha? Vamos resolver essa questãozinha aí que nos pede a carga crítica. Pra começar é importante frisar que o problema nos diz que a coluna está apoiada em pinos, logo a equação da carga crítica é:
O problema nos disse que é um aço , que tem , e também forneceu o comprimento da coluna de . Então para achar a carga crítica basta a gente calcular o momento de inércia e substituir na equação!
Passo 2
Antes de sair calculando o momento de inércia igual a uns loucos vamos pensar um pouco...

Uma seção transversal, assim como a fornecida pelo problema, tem diferentes momentos de inércia dependendo do eixo a qual estamos analisando. A flambagem sempre vai acontecer no eixo mais fraco, beleza?
Mas você, que é muito inteligente que eu sei, já percebeu que a figura é simétrica então o momento de inércia em é igual ao momento de inércia em . Ahhh, então suave, nesse caso não precisamos nos preocupar muito com a direção, portanto:
Agora para calcular a gente tem uma figura composta por duas barras, então vamos calcular cada barra separadamente e somar os momentos resultantes:
Aí aqui não tem muito segredo, a base de uma é igual a altura da outra, logo:
E
Passo 3
Agora é só substituir na equação da força crítica:
Passo 4
Pessoal, a gente já até achou a carga crítica mas é importante também saber se não ultrapassamos o limite de escoamento do material também. Como o aço tem , então a gente vai fazer:
A área da seção eu vou calcular como um quadradão () menos 4 quadradinhos :
Então vamos ter:
Como essa tensão é menor do que então a nossa coluna pode ser utilizada no projeto já que não irá flambar e nem escoar =D
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.5
Uma barra quadrada é feita de plástico com módulo de elasticidade e deformação por escoamento . Determine as dimensões de sua menor seção transversal, de modo que não falhe por flambagem elástica. As extremidades estão presas por pinos e seu comprimento é .
Passo 1
Fala aí, meninada marota!
Para começar alguns de vocês podem ter ficados espantados com o termo flambagem elástica, mas não se espantem, isso é exatamente o que temos estudado então não se preocupem!
O que o problema quer é a dimensão da área da seção transversal, então se fizermos um desenhozinho vamos ter isso aqui:
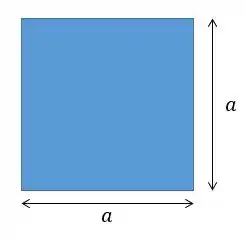
Correto? O problema disse que é um quadrado né? Show of ball...
A equação da flambagem para extremidades apoiadas em pinos é:
O problema até forneceu , e de certa forma pede (que depende da dimensão ). Mas o problema não forneceu , não é mesmo?
Mas reparem que o problema nos deu esse termo de deformação por escoamento, e se a gente for trazer dos nossos conhecimentos de escoamento vamos lembrar que:
Com esse equação a gente pode achar o tensão de escoamento e pela tensão achar a carga crítica. Então vamos resolver?
Passo 2
Vamos começar então tentando descobrir quem é a nossa força crítica e para isso mas analisar a tensão de escoamento:
Como o problema nos deu e então basta substituir:
Vamos guadar essa informação e analisar a flambagem.
Passo 3
Vamos substituir o que temos na equação da flambagem e ver no que dá:
Sendo que o momento de inércia de um quadrado de lado é igual a:
Subsituindo:
Chegamos em algum lugar interessante, mas ainda não dá para resolver o problema. O que fazer então?
Como o problema quer a menor dimensão possível de , então nós vamos calcular a tensão crítica de flambagem:
Como a área é:
então:
Passo 4
Como o problema quer o menor possível então nós vamos ter que igualar a tensão crítica de flambagem com a tensão de escomento:
Nesse caso a gente nem precisa fazer a verificação do limite de escoamento, porque ao igualar as duas equações a gente já assumiu que vale para ambas.
Resposta
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.8 (adaptada)
Uma coluna de aço tem comprimento de e está apoiada por pinos em ambas as extremidades. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
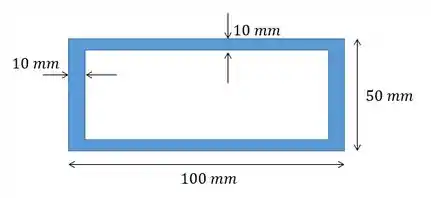
Passo 1
Bom, pessoal, vamos lá resolver mais um exercício! Esse aqui não tem muitos segredos é só lembrar que a equação da flambagem para extremidades apoiadas em pinos é:
Aí temos de lembrar também que o coeficiente de elasticidade do aço é . Além disso o problema forneceu os dados: e nos deu a seção transversal para calcularmos .
Então basta calcular e substituir na equação, aí acabou!
Passo 2
Vamos calcular o momento de inércia. Percebam que temos dois eixos:
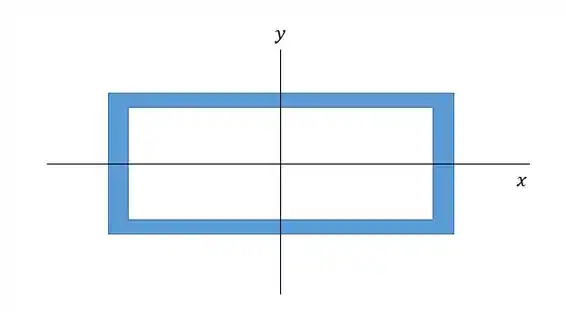
Como trata-se de um retângulo nós vamos ter que o momento de inércia emc ada eixo é diferente, aí a gente tem que lembrar que a flambagem ocorre no eixo de menor momento de inércia.
A equação do momento de inércia para uma barra retangular é:
Se nos queremos o menor momento de inércia então devemos escolher o menor lado para ser a altura (já que a altura que está sendo elevada ao cubo). Isso faz sentido não faz? Logo, vamos ter que a base vai ser o nosso eixo mesmo e a altura no eixo .
Mas a nossa seção é vazada então devemos subtrair o termo de dentro:
Passo 3
Agora é só substituir na equação da flabagem:
Passo 4
Pra finalizar vamos ver se a nossa barra resiste ao escoamento por compressão:
Calculando a área nós temos:
Como a tensão de escoamento do aço é então a carga de pode ser aplicada à coluna sem risco de escoar.