Método da superposição
Produzido por Pablo RicardoTeoria
Fala, galerinha!!
Hoje a gente vai bater um papo sobre o método da superposição aplicado de modo a achar as reações em vigas e eixos estaticamente indeterminados. Por exemplo o caso abaixo:
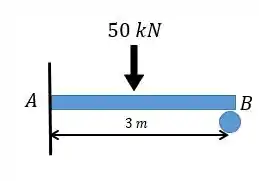
Se você tem nos acompanhado deve lembrar de um exercício parecido e que já resolvemos ele utilizando o método dos momentos de área onde utilizamos o diagrama . Mas agora eu te pergunto uma coisa, será que é realmente necessário sempre fazer esse diagrama para resolver problemas assim?

A resposta é NÃO! Não precisamos ficar toda hora achando os diagramas até porque isso é chato pra caramba não é verdade?
Então se liga que eu vou te ensinar um jeito boladão de resolver problemas sobre vigas e eixos estaticamente indeterminados.
Problema estaticamente indeterminado
Vamos utilizar o exemplo dado a cima e visualizar que se trata de um caso de hiperestaticidade, ou seja, estaticamente indeterminado. Isso porque temos mais incógnitas do que equações.
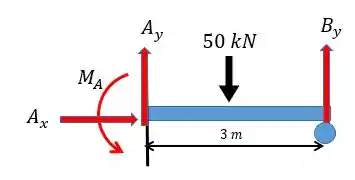
Para resolver isso a gente usa nossos conhecimentos sobre linha elástica que nos fornecerá o valor de uma incógnita, assim vamos ter o mesmo número de incógnitas e equações podendo pelas equações da estática normalmente =D
Separando as componentes
Agora vamos retirar um apoio e substituí-lo por uma força.
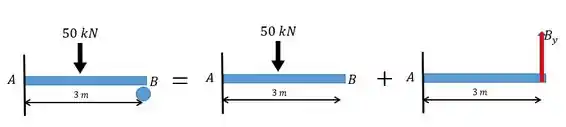
Galera, a gente só tem que lembrar de uma coisa: a nossa viga tem que continuar em equilíbrio então se a gente retirar o engaste teríamos de adicionar as duas forças correspondentes e o momento correspondente (por isso é mais prático retirar o apoio).
Quando a gente fala de linha elástica a gente pode fazer a superposição das deflexões que consiste em calcular a deflexão de cada componente separadamente e fazer uma simples soma algébrica entre eles.
Relação entre as deflexões
Para cada carregamento diferente vamos fazer o cálculo da respectiva deflexão. Primeiro vou mostrar graficamente como fica e depois vamos achar os valores.
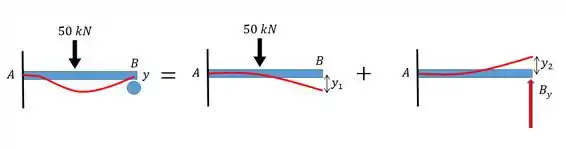
Reparem que no nosso exemplo a viga “real” exibida na extrema esquerda não possui deflexão em , ou seja.
Enquanto nas componentes separadas há uma deflexão para cima e outra para baixo . Dessa forma vamos ter que:
Logo, a deflexão de uma é exatamente o oposto da outra!
Cálculo das deflexões
Pessoal, para calcular o valor de e nós podemos utilizar qualquer um dos métodos que são utilizados no calcula da linha elástica podendo ser: interação, momentos de área ou superposição. Sério, tanto faz!

Como tanto faz eu vou usar o método mais fácil que é a utilização da tabela!!! Essa tabelinha tem o nome de “inclinações e deflexões em vigas” e é encontrada em qualquer livro de resistência dos materiais. Abaixo está o que precisamos para o nosso problema.
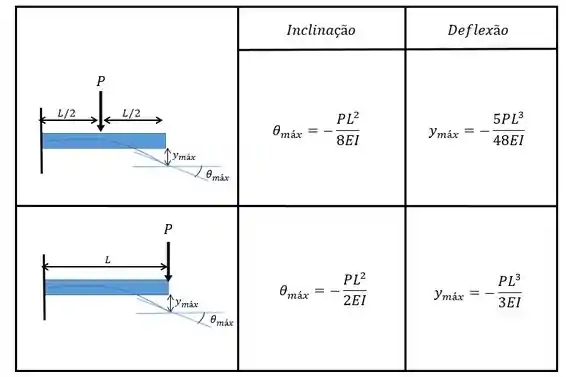
Com isso vamos achar os valores:
e
Repara que ficou positivo porque a força está voltada para cima!
Substituindo os valores a gente vai achar:
e
Aplicar na equação que a gente achou que relaciona as deflexões:
Achamos o valor de uma das reações!!!
Achando as outras reações
Com o valor de podemos agora com a a estática podemos achar o resto!
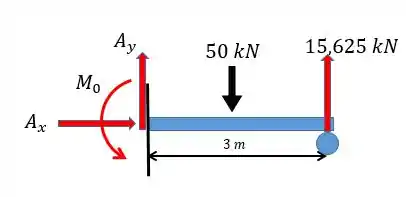
Resumo
Logo, para que a gente possa utilizar o método da superposição temos de seguir o seguinte passo a passo:
- Separar os componentes.
- Achar a relação entre as deflexões a partir da geometria do problema.
- Calcular o valor de cada deflexão individual com o método mais conveniente.
- Aplicar a relação entre as deflexões para os valores encontrados.
- Achar o valor de uma das reações.
- Achar as outras reações pelas equações da estática.