Inclinação e deslocamento pelo método dos momentos de área
Produzido por Pablo RicardoTeoria
Meus queridos e minhas queridas que tal aprendermos mais um método para o cálculo da inclinação e deslocamento da linha elástica?
A gente já viu como fazer isso por integração e agora vamos aprender a fazer por meio da área do diagrama de momento fletor! Até porque né, áreas e integrais tem tudo a ver não é mesmo?

Pessoal, este tipo de método sempre vai achar a diferença entre as inclinações de dois pontos da viga. Nunca o valor absoluto, ok? Então dá uma olhada no exemplo abaixo para ficar um pouco mais concreto para você!
Diferença entre inclinações
Vamos pegar o exemplo de uma viga biapoiada com uma carga central sendo exercida sobre ela.
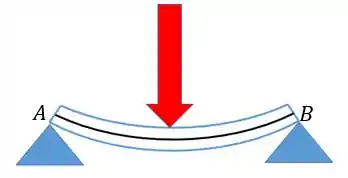
Nesse desenho a gente já representou a deflexão que a viga está sofrendo. Agora vamos imaginar que queremos calcular a inclinação do ponto em relação ao ponto central.
Uma forma melhor de ver essa viga é representar apenas a linha elástica e a inclinação em e no centro , da seguinte forma.

Viram que a inclinação de em relação à inclinação de é dada pelo ângulo , formado pelas duas retas tangentes?
É exatamente esse ângulo que vamos achar quando aplicarmos o conceito das áreas. É importante lembrar também que não vamos achar o ângulo de ou mas o ângulo entre os dois!
Agora vamos para a parte das contas..
Equação da linha elástica
Pessoal, a gente já viu a equação da linha elástica mas pra refrescar a memória vou colocar de novo aqui pra vocês.
Onde é o próprio deslocamento, ou deflexão, da linha elástica. e são a constante elástica e o momento de inércia e o momento fletor.
Além disso a gente tem também a equação da inclinação, que é nada mais nada menos do que a primeira derivada dessa joça aí:
Show de bola, agora que a gente relembrou essas equações a gente vai ver como elas vão se tornar áreas. Deixa eu te fazer uma pergunta, como você calcularia a área da função dada abaixo entre os pontos e ?

Você, que é um excelente aluno de cálculo que eu seeei, vai fazer a integral dessa função entre e :
E você vai estar certo!! Uhulll que felicidade =D
Cálculo da inclinação pela área
Agora imagina que a gente constrói o seguinte gráfico:
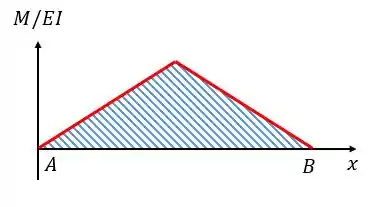
A área desse gráfico vai ser igual a:
Repare que isso é idêntico à equação da inclinação!
Então a gente pode dizer que a inclinação entre dois pontos da nossa viga é igual a área do diagrama !!! Colocando na forma de uma expressão:
A gente pode escrever ainda que a diferença entre esses dois ângulos pode ser escrita como:
Agora que tal ver isso para o deslocamento?

Cálculo do deslocamento pela área
Pessoal, no caso do deslocamento a gente não vai usar a área apenas, vamos utilizar o momento da área. Assim, vamos precisar achar o baricentro de área também!
Nesse caso também vamos achar um deslocamento entre dois pontos, ok? E não o valor absoluto!
Colocando na forma de uma equação vamos ter:
Reparem que o termo sai da integral e se torna que é o próprio centroide! Além disso essa equação é obtida de algumas aproximações considerando que os ângulos e deflexões são muito pequenos. Mas o principal para você agora é saber que a deflexão pode ser calculada pelo momento da área.
Podemos escrever ainda:
Onde é o deslocamento, ou deflexão, relativo(a) entre e . é o centroide da área e é a inclinação relativa entre e (que é igual a área).
Vamos fazer um exemplo!
Exemplinho
Imaginem que construímos o seguinte diagrama . Que é o diagrama de momento fletor mas dividido pelos termos e , beleza?
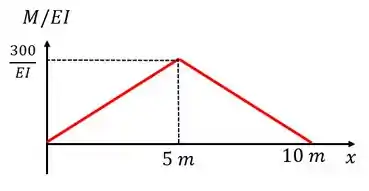
Se a gente quiser achar a inclinação entre os pontos e . A gente só precisa achar a área da figura formada:
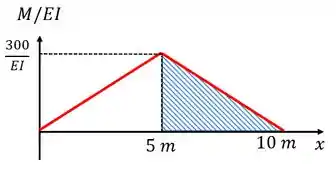
Tranquilo né? Aqui é válido lembrar também dois pontos:
- Esse valor do ângulo é dado em radianos quando utilizadas grandezas no sistema internacional []
- Valores positivos representam variações no sentido anti-horário, enquanto valores negativos representam variações no sentido horário
Agora vamos achar também o deslocamento relativo entre os dois pontos. Lembre-se que para isso temos de achar o centroide:
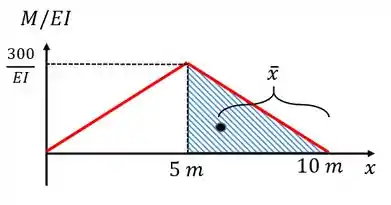
Vamos frisar três pontos importantes aqui também:
- O valor do deslocamento é dado em metros quando utilizadas grandezas no sistema internacional []
- Valores positivos representam deflexões acima da linha tangente, enquanto valores negativos representam deflexões abaixo da linha tangente.
- A distância do baricentro é calculada em relação ao primeiro ponto do termo , ou seja entorno do ponto . No nosso caso e . Isso é muito importante e faz toda a diferença no final!
Equação da linha elástica
Cálculo da inclinação pela área
Cálculo do deslocamento pela área
Exemplinho
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.55
Determine a inclinação e a deflexão em . é constante.
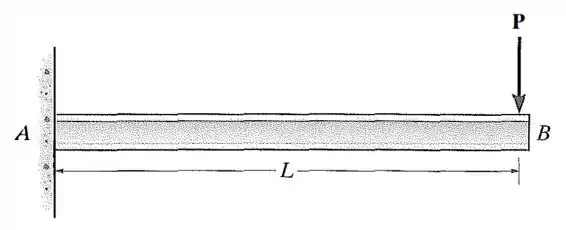
Passo 1
Pessoal, aqui o problema pede para calcular a inclinação que é dada por e a deflexão que é o termo ou , aqui vamos usar . Existem diversas formas de fazer isso mas vamos utilizar a técnica dos momentos de área.
A gente viu dois teoremas que vão nos ajudar o primeiro é para calcular a inclinação. Para isso basta achar a área embaixo do gráfico
Já para achar a deflexão é só pegar o termo que achamos no item acima e multiplicar pelo centroide da área.
Vamos fazer o passo a passo.
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
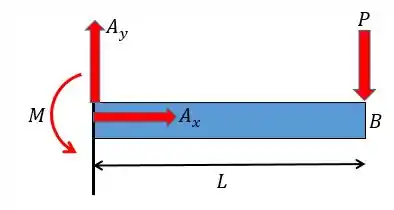
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Passo 3
Agora vamos colocar essas forças na viga:
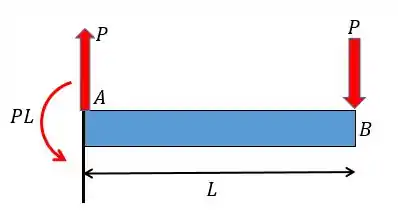
O diagrama ficará da seguinte forma:
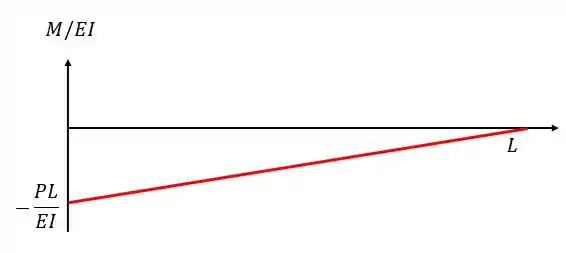
Nesse caso o valor máximo (em módulo) é em , vale e vai se aproximando de zero linearmente até chegar em em
Passo 4
Agora vamos aplicar o primeiro teorema para achar a inclinação em . Para isso é legal construir um esboço de como a deflexão da viga vai ficar:

Para achar esse valor de , que é a inclinação de em relação à inclinação de vamos calcular a área embaixo do gráfico entre e , desta forma vamos ter:
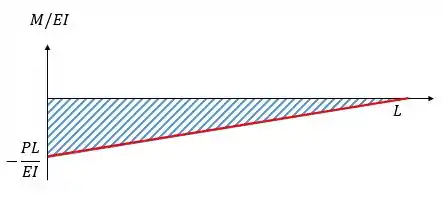
Como não existe inclinação em pelo fato da viga estar engastada então vamos ter:
Assim já temos a inclinação e vale:
Passo 5
Para achar a deflexão basta multiplicar o termo pelo centroide de área que acabamos de utilizar.
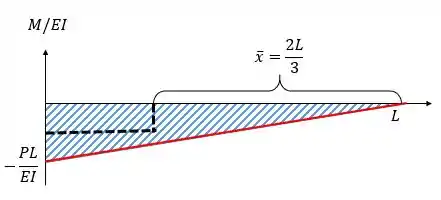
Como o centroide de um triângulo está localizado a uma distância de da extremidade, vamos ter:
obs: Reaparem que precisamos pegar a distância a partir do ponto , pois estamos calculando . Se estivéssemos calculando pegaríamos a distância a partir do ponto .
Assim a deflexão será igual a:
Novamente pelo motivo da viga estar engastada vamos ter que a deflexão é nula em portanto:
Repare que ambas respostas deram negativas, o que faz sentido já que tanto a inclinação quanto a deflexão estão abaixo da tangente de .
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.58
Determine a inclinação em e a deflexão em . é constante.
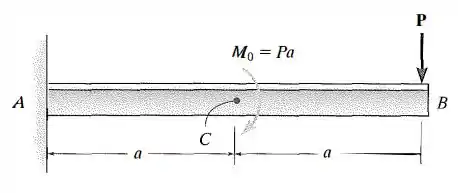
Passo 1
Para achar a inclinação e a deflexão nós vamos utilizar os dois teoremas vistos, lembrando que tanto a inclinação quanto a deflexão são iguais a zero no ponto de engaste.
Antes de mais nada é muito importante que façamos o diagrama do momento fletor e depois vamos calcular a área para achar a inclinação.
Por fim vamos multiplicar a área pelo centroide da área afim de achar a deflexão!
Passo 2
A primeira coisa que temos de fazer então é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
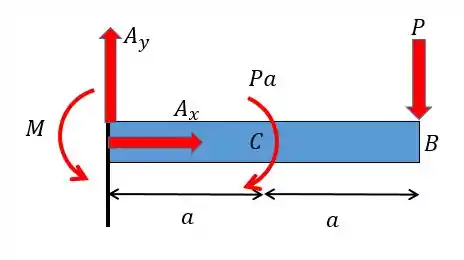
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Passo 3
Agora vamos colocar essas forças na viga:
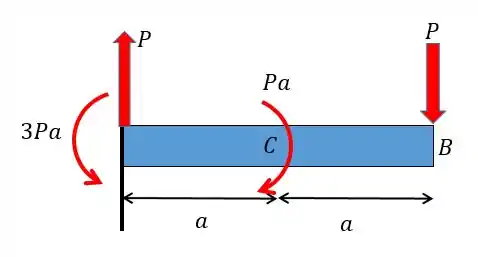
No trecho nós vamos ter que a força cortante vai valer:
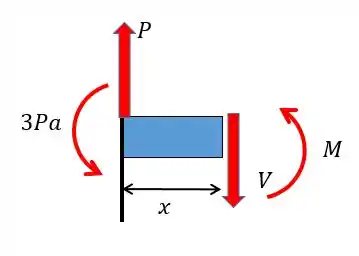
E o momento fletor:
No trecho vamos ter que a força cortante vai valer:
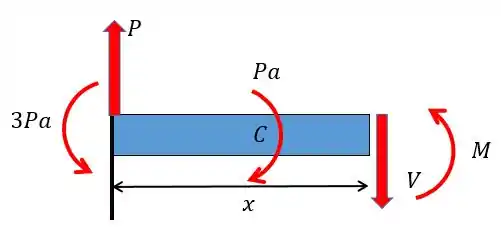
E o momento fletor:
O diagrama ficará da seguinte forma:
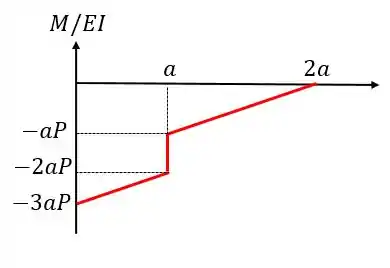
Passo 4
Agora vamos aplicar o primeiro teorema para achar a inclinação em . Para isso é legal construir um esboço de como a deflexão da viga vai ficar:
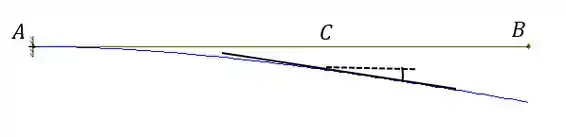
Dando um zoom no ponto vamos obter o seguinte:
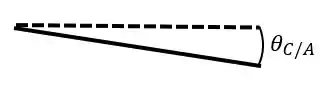
Onde a reta pontilhada é a tangente de (ela tem inclinação zero porque está engastado) e a reta contínua é a tangente de , a gente quer o ângulo entre as duas.
Para achar esse valor de vamos calcular a área embaixo do gráfico entre e , desta forma vamos ter:
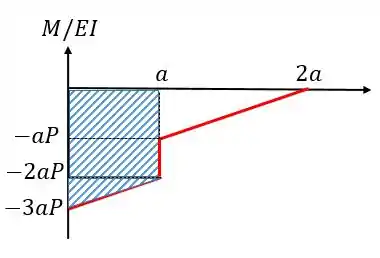
Como não existe inclinação em pelo fato da viga estar engastada então vamos ter:
Assim já temos a inclinação e vale:
Passo 5
Agora vamos calcular a deflexão em para isso a gente tem que achar a inclinação em , ou seja a área do gráfico abaixo.
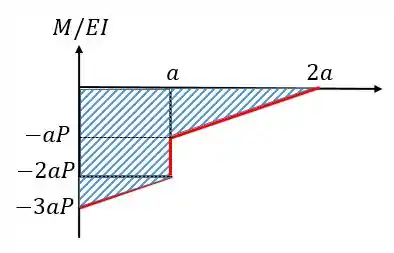
A área vai ser igual a:
Agora, para achar a deflexão precisamos também do centroide da área. Calculando esse centroide vamos ter:
Lembre-se que a posição do centroide tem o o ponto como referência!
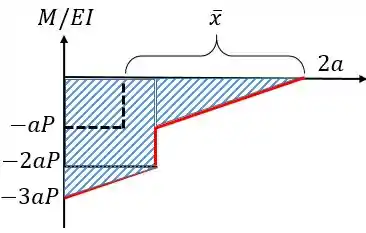
Para facilitar vamos encontrar a posição do centroide de cada uma das três figuras (os dois triângulos e o retângulo) em relação à origem:
Podemos cortar um e o termo :
Mas como queremos em relação à e não em relação à origem vamos ter:
E agora é só multiplicar na área
Vamos obter:
Resposta
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.59
Uma ginasta de está em pé no centro da trave (viga) de equilíbrio simplesmente apoiada. Se a trave for feita de madeira e tiver aseção transversal mostrada na figura, determine a deflexão máxima. Consideramos que os apoios em e em são rígidos. .
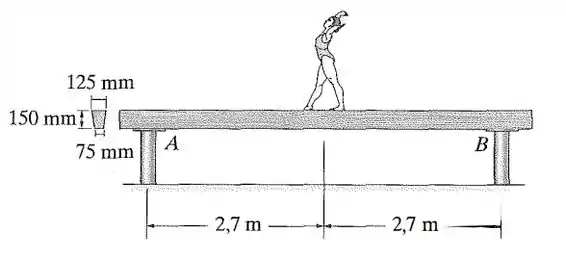
Passo 1
Galerinha, esse problema é muito parecido com os anteriores e pede a deflexão máxima. A partir daí já podemos saber que essa deflexão máxima ocorre no centro da viga, pelo fato de existir apenas um carregamento central, o peso da ginasta.
Além disso é válido lembrar também que a pesar de não haver inclinação nos apoios, existirá inclinação em ambos. Isso é importante para a resolução.
Vamos começar o problema que nem sempre e fazer um esquema de forças e achar o diagrama do momento fletor.
Partiu!
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
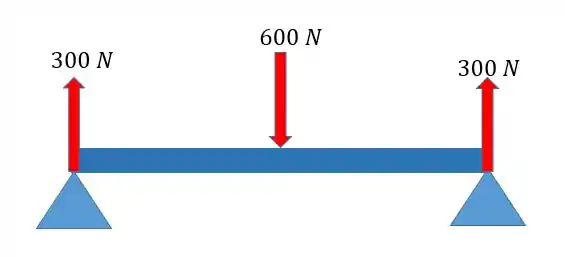
Pessoal, já coloquei direto os valores das reações porque elas tem que ser iguais. Logo se a gente tem uma carga central de então cada reação tem o valor de , ok?
Passo 3
Agora podemos fazer o diagrama de momento fletor, fazendo um corte na barra vamos obter:
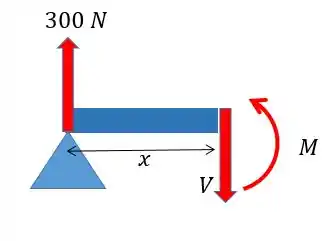
Para achar a força cortante:
Para achar o momento fletor:
O diagrama é simétrico e possui valor máximo em , assim podemos obter:
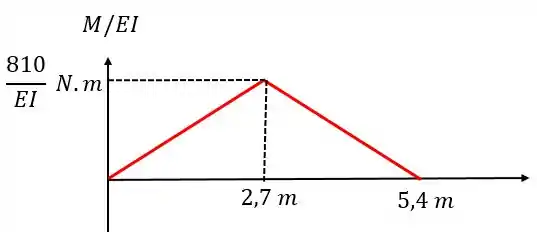
Pessoal, reparem que aqui temos o diagrama do momento fletor sobre , não apenas do momento fletor!
Passo 4
Agora vamos calcular a deflexão máxima, que ocorre no centro. Para isso vamos calcular a área do diagrama que fizemos de modo a achar primeiro a inclinação no ponto médio.
Gente, nessa etapa tentem sempre fazer um esboço da linha elástica, nesse caso vai ficar assim:

Olha só agora como ficou! A tangente em que é nula neste caso, enquanto a tangente em tem uma inclinação. Gente, isso faz sentido dadas as condições de contorno né? (Uma viga simplesmente apoiada vai ter inclinação nas pontas. Como a carga é simétrica o centro não tem inclinação).
De qualquer forma vamos poder calcular o termo da inclinação de com relação à :
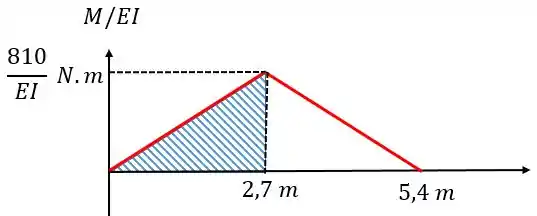
Assim, vamos ter que:
Lembrando que:
Como a inclinação de é nula, vamos ter que:
Passo 5
Agora a gente vai terminar esse problema com um pouquinho de geometria, se liga:
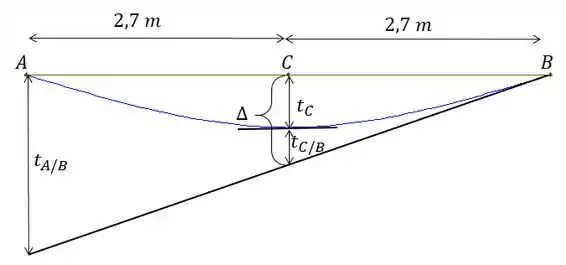
O que queremos achar é a deflexão em , ou seja, . A partir da geometria da figura a gente tem que:
Onde poder ser achado por semelhança de triângulos (um com base de e outro com base de ):
Logo, podemos calcular como:
Agora só precisamos achar e . Para isso vamos voltar ao nosso diagrama. Calculando primeiro vamos ter:
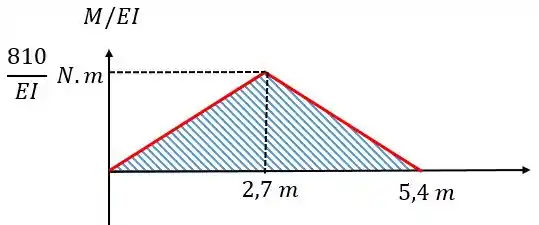
Agora vamos calcular :
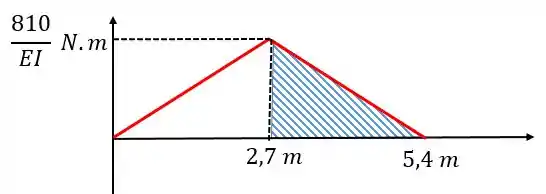
Passo 6
Agora é só juntar os termos:
Assim vamos ter:
Mas ainda falta substituir os termos e .
Passo 7
Calculando o momento de inércia:
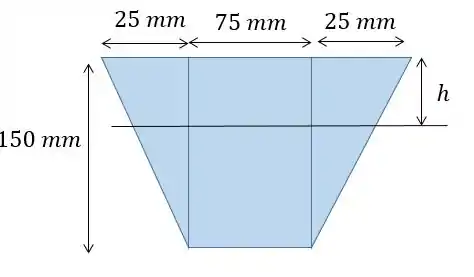
Essa equação aí é tabelada ta bom, pessoal?
Agora é só fazer o momento de inércia de cada figura com relação ao eixo que passa pelo centroide, ou seja, a altura h da base maior do trapézio. Dividindo o trapézio em 2 triangulos e 1 retângulo, o momento de inércia dos triângulos é:
Agora para o retângulo:
O momento de inércia total vale:
Agora é só substituir:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.54 (Adaptada)
Determine a deflexão em . é constante.
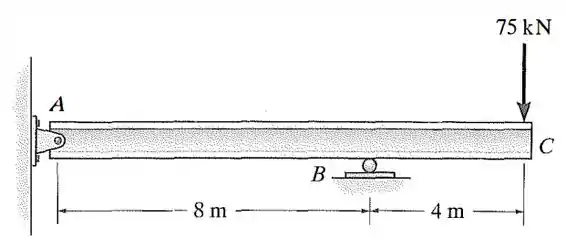
Passo 1
E aí, pessoal!!
Essa questão já um pouquinho mais complexa porque, apesar de pedir as mesmas coisas (inclinação e deflexão) aqui não há engaste. Ou seja, quando a gente for calcular a inclinação utilizando o método da área e vamos ter algo do tipo:
Sendo que agora existe uma inclinação em .
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
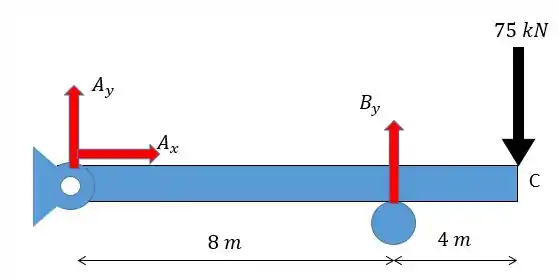
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Dessa forma:
Passo 3
Agora vamos colocar essas forças na viga:
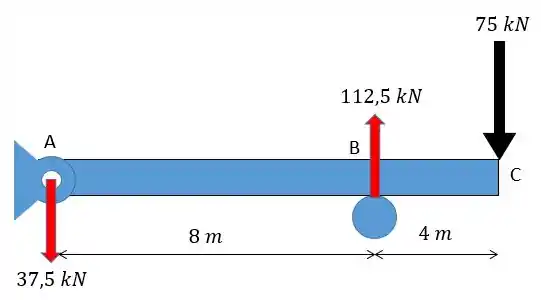
Como só existem forças pontuais o momento fletor cresce e decresce de forma linear tendo o seu máximo no ponto máximo em . Fazendo o corte na seção vamos obter:
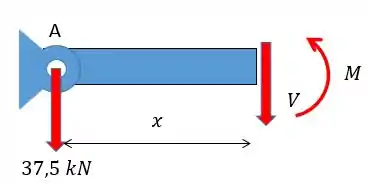
Para achar a força cortante:
Para achar o momento fletor:
Assim, o diagrama ficará da seguinte forma:
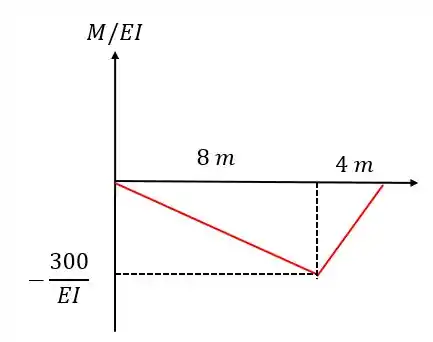
Passo 4
Pessoal, lembram que
Dessa forma a gente precisa saber qual é a inclinação de também.
Gente, vamos resolver esse problema com ajuda na nossa amiga geometria. Que tal fazermos um esboço da linha elástica olha só!
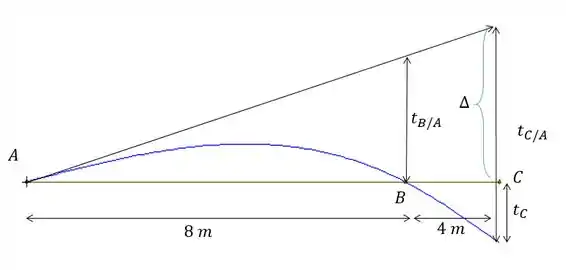
Com isso a gente percebe, pela geometria da figura que:
E esse delta pode ser encontrado por meio de uma semelhança de triângulos (olha para os triângulos de base 8 e 12):
Assim vamos ter:
Dessa forma precisamos achar:
e
Passo 5
Achando :
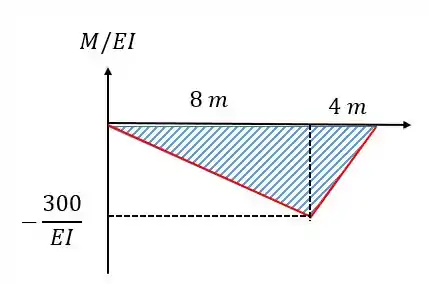
A área é igual a:
O centroide vai estar localizado em:
Mas esse é o valor a partir da origem, nós queremos a partir de , logo:
Assim vamos ter que:
Passo 6
Agora vamos calcular :
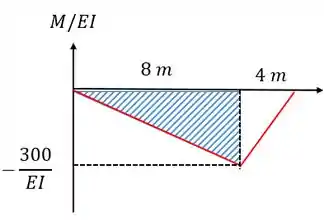
A área é igual a:
O centroide está localizado em:
Assim, vamos ter que:
Passo 7
Agora é só juntar os dois termos:
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.61
A viga está sujeita à carga mostrada na figura. Determine a inclinação em e o deslocamento em . Considere que o apoio em é um pino e em , um rolete. é constante.
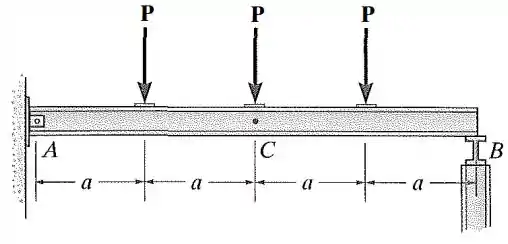
Passo 1
Vamos lá, galera, como essa viga tem um pino e um rolete como apoio, ambos vão ter um deslocamente nulo. Porém, existirá uma inclinação não nula nesses pontos.
O problema pede exatamente a inclinação em (pino) e o deslocamento em . Para isso vamos utilizar o nosso método das áreas.
Primeiro vamos construir o diagrama do momento fletor. Apartir desse diagrama a área será a inclinação e o momento da área o deslocamento. Então partiu?
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
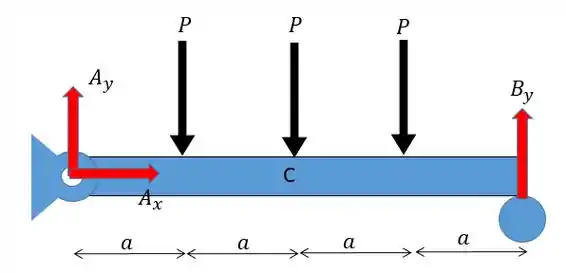
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
Aqui a gente pode lembrar que se trata de um carregamento simétrico então vamos ter que assim:
Passo 3
Agora vamos colocar essas forças na viga:
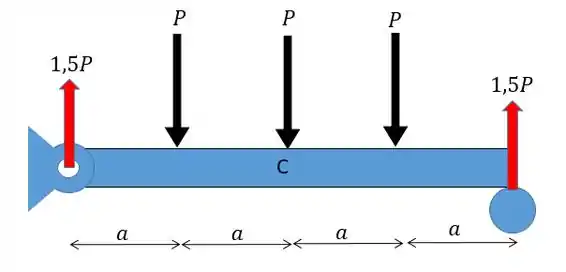
Assim, o diagrama ficará da seguinte forma:
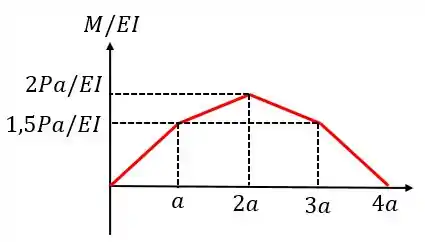
Passo 4
Pessoal, lembram que
Mas como estamos falando de uma viga simétrica então vamos ter que a inclinação no centro é nula.
Logo,
Então basta calcular a área do gráfico entre e :
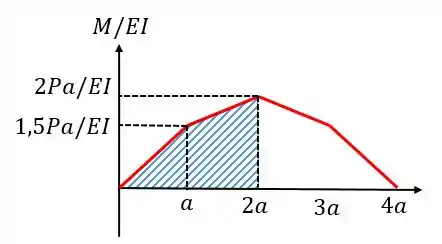
Passo 5
Agora, como o deslocamento em é nulo, para achar o deslocamento em basta fazer:
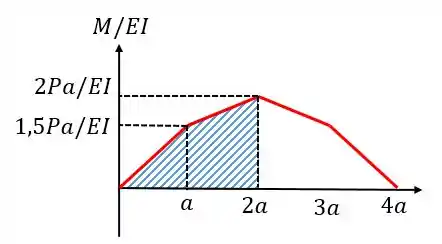
primeiro vamos achar o centroide da figura, para isso vou dividir em um retângulo e dois triângulos:
Simplificando por :
Desta forma vamos ter:
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 448. Problema 12.60
O eixo é suportado por um mancal de apoio em , que exerce somente reações verticais sobre o eixo, e por um mancal de enconsto em , que exerce reações horizontais, bem como reações verticais sobre o eixo. Determine a inclinação do eixo nos mancais. é constante
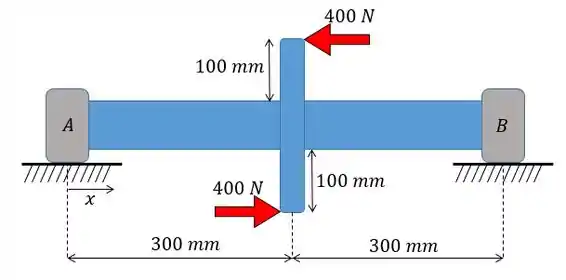
Passo 1
Fala galera! Temos um probleminha aqui bem legal né, bem prático!? Vamos entender um pouco mais sobre esse problema, temos um eixo submetido a ação de duas forças que juntas causam um momento.

E esse momento aplicado ao eixo, assim como a maioria dos carregamentos irá causar uma deformação. Logo, o estudo da linha elástica faz total sentido aqui e o problema pede o valor da inclinação que esse momento causa. Então vamos utilizar a seguinte relação:
Como podemos ver é necessário utilizar o momento fletor então a primeira coisa que vamos fazer é montar o diagrama . Partiu?
Passo 2
A primeira coisa que temos de fazer então é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga:
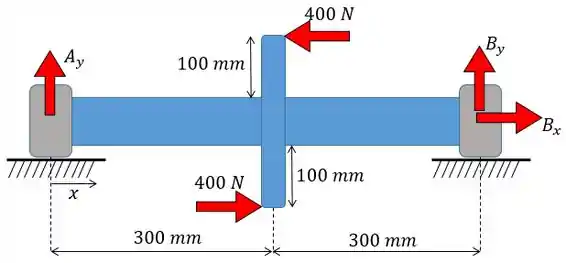
Fazendo o somatório das forças em :
Agora fazendo o somatório das forças em :
Fazendo o somatório dos momentos em relação ao ponto e considerando o sentido anti-horário positivo:
Meus amores aqui vai uma diquinha para vocês, como dito anteriormente a dupla de forças irá realizar um momento, na real essa dupla de forças é considerar um binário e para achar o momento desse binário é só multiplicar a força pela distância entre elas.
Caso você prefira fazer cada força separadamente pode fazer, ok? Esse binário não é nada demais e se não te ajudar você não precisa fazer =D
Voltando ao somatório dos momentos:
Logo,
Passo 3
Agora vamos colocar essas forças na viga:
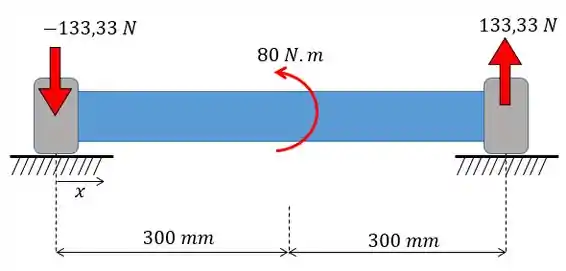
E vamos obter o seguinte diagrama . (Aqui vale lembrar também que esse diagrama é idêntico ao diagrama só do momento fletor já que está dividido por uma constante).
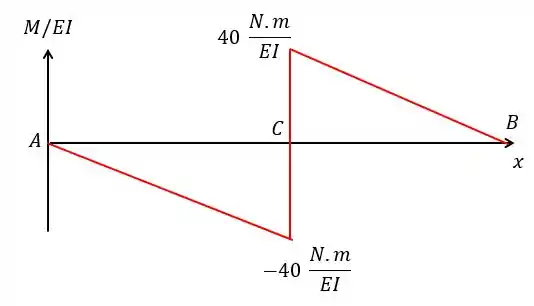
Passo 4
Meus abiguinhos lindos, agora só falta aplicarmos a nossa equaçãozinha!!!
Tá mas e aí quais pontos e eu vou escolher? Que tal pergarmos o ponto médio e a extremidade , assim a nossa equação vai ficar:
Calculando a área entre e e utilizando as medidas em :
Agora vamos fazer entre e e vamos obter:
Somando as duas equações a gente pode achar:
O que faz sentido já que é um problema simétrico, mas não nos fornece nenhum dado muito válido. Logo, vamos analisar o problema a partir das deflexões.
Passo 5
A equação da deflexão é:
Assim vamos achar a deflexão relativa entre e :
Mas essa é a deflexão relativa, a deflexão real entre eles é nula, a gente consegue ver isso com ajuda de um esboço. Aqui repara que vamos utilizar a aproximação , beleza? Podemos fazer isso porque quando falamos de linha elástica temos ângulos bem pequenininhos =D
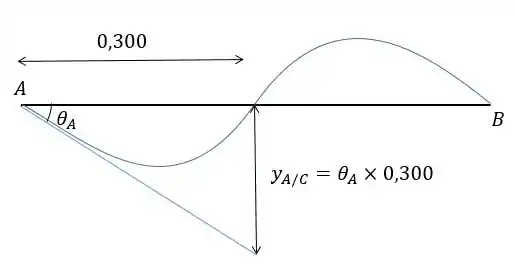
Então a nossa equação é:
Dessa forma vamos ter:
Como ambos os ângulos são iguais então os dois valem:
Resposta
Exercício Resolvido #7
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 845. Exercício 8 – 16 (Adaptada)
Para a viga com carregamento mostrado, determinar a declividade do ponto . é constante.
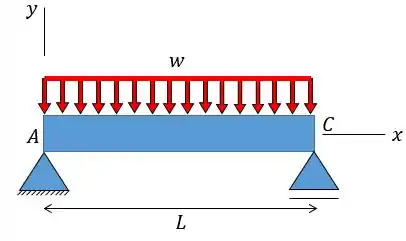
Passo 1
Faaala, galerinha!! Esse problema pede para calcularmos a declividade tanto do ponto quanto do ponto . Se estamos falando de declividade então estamos falando de ângulo e logo vamos trabalhar com as áreas do diagrama , belezinha? Lembrando que:
Aqui utilizamos e mas podem ser quaisquer dois pontos.
A primeira coisa que vamos fazer netão é montar o diagrama do momento fletor. Depois disso basta calcular a área (tomando alguns cuidados que vou te explicar mais pela frente) e um abraçooo.
Partiu?
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga assim como as forças concentradas de cada carregamento distribuído:
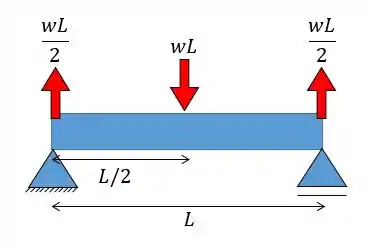
Pessoal, a gente nem precisou fazer muita conta levando em consideração que esse é um problema simétrico não é mesmo? Cada reação é igual à metade do carregamento.
Passo 3
Com o carregamento a gente pode desenhar o diagrama :
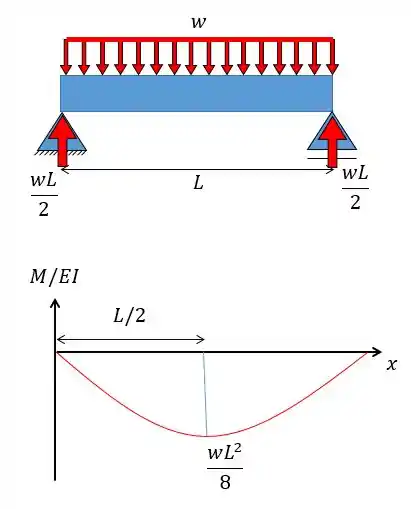
Passo 4
Pessoal, o problema pede a declividade do ponto correto? Então faz sentido fazermos:
Onde é o ponto central da barra. Mas agora vale a observação de que no ponto central a angulação é nula, logo:
Basta calcular a área do gráfico entre e :
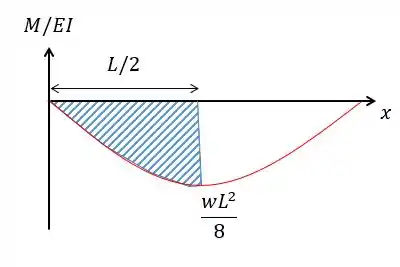
Galerinha, a gente agora só precisa lembrar que para uma parábola nós vamos calcular a área conforme a base e a altura:
Como queremos apenas metade da parábola vamos ter:
Logo vamos ter:
Então no final vamos ter:
Incuímos o sinal negativo porque a área está abaixo do eixo .
Resposta
Exercício Resolvido #8
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 845. Exercício 8 – 15 (Adaptada)
Para a viga com carregamento mostrado, determinar a declividade relativa entre e . é constante.
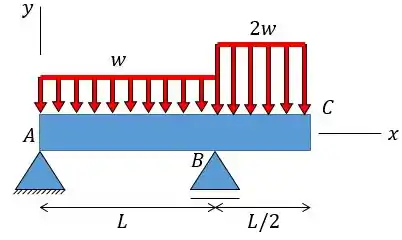
Passo 1
Faaala, galerinha!! Esse problema pede para calcularmos a declividade relativa entre e . Se estamos falando de declividade então estamos falando de ângulo e logo vamos trabalhar com as áreas do diagrama , belezinha? Lembrando que:
Aqui utilizamos e mas podem ser quaisquer dois pontos.
A primeira coisa que vamos fazer netão é montar o diagrama do momento fletor. Depois disso basta calcular a área (tomando alguns cuidados que vou te explicar mais pela frente) e um abraçooo.
Partiu?
Passo 2
A primeira coisa que temos de fazer é construir o diagrama de momento fletor para a nossa viga. Para isso vamos desenhar as forças de apoio dessa viga assim como as forças concentradas de cada carregamento distribuído:
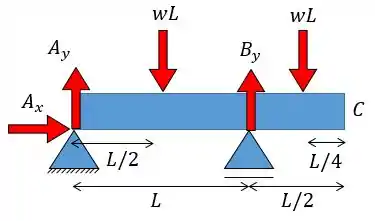
Como só existe uma força em então:
Agora fazendo o somatório das forças em :
E aplicando o somatório dos momentos fletores em vamos ter:
E consequentemente vamos ter:
Passo 3
Agora vamos ver o carregamento na viga:
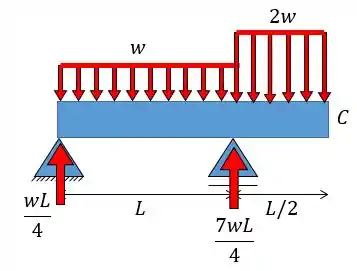
O momento fletor será dado pelas seguintes equações:
Assim, o diagrama ficará da seguinte forma:
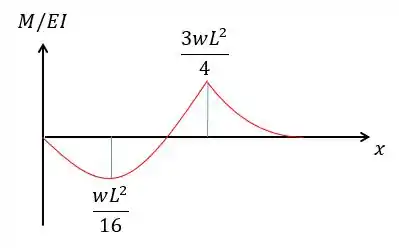
Passo 4
Pessoal, o problema pede a declividade relativa entre e correto? Então faz sentido fazermos:
Basta calcular a área do gráfico entre e :
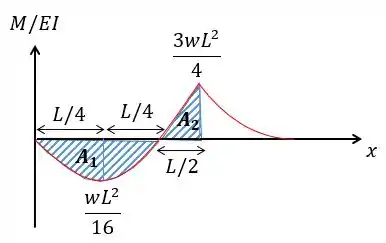
Galerinhaaa, eu sei que o tamanho de ficou menor do que no desenho mas relavaaaa por favor kkkkk foi só um problema técnico...
Galerinha, a gente agora só precisa lembrar que para uma parábola tipo a nós vamos calcular a área conforme a base e a altura:
Logo vamos ter:
Já para a parábola referernte à nós vamos ter que a área é dada também em função de sua base e sua altura mas da forma:
Então no final vamos ter: