Superposição de efeitos
Teoria
Oiii, pessoas!!
A gente já viu algumas formas de calcular a inclinação e deflexão de um ponto numa viga. Hoje não vai ser diferente!! Vamos ver mais um método para esse tipo de cálculo, esse método é chamado de método da superposição.
Esse método é maneiro porque não foca muito nas contas e teorias já que utiliza tabelinhas!
Para exemplificar vamos imaginar o seguinte problema: calcular a inclinação e deflexão do ponto médio da barra submetida a uma força e um carregamento distribuído :
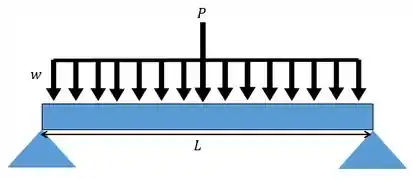
Identificando os carregamentos
A primeira coisa que devemos fazer é identificar e separar os carregamentos. Para o exemplo a cima a gente vai ter:
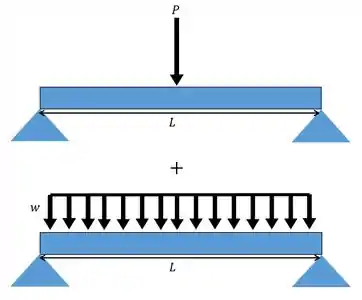
A gente ainda pode representar a linha elástica com o ângulo e a deflexão que queremos:
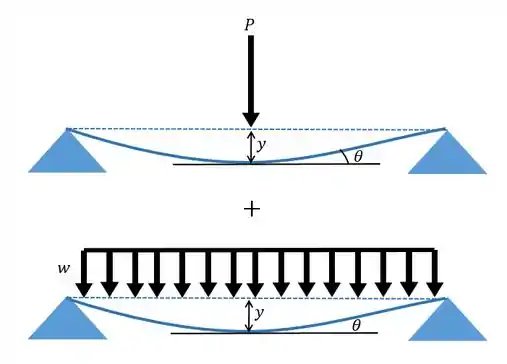
Fazendo o cálculo
Beleza galerinha. Agora que a gente já tem uma boa ideia de como a nossa viga fica, a gente tem que fazer os cálculos né? Por isso a gente vai utilizar uma tabela padronizada, essa tabelinha na verdade é uma tabelona com várias situações de carregamento e de apoio. Além disso a tabela mostra também as inclinações de deslocamentos. Aqui vou apresentar apenas dois casos para vocês.
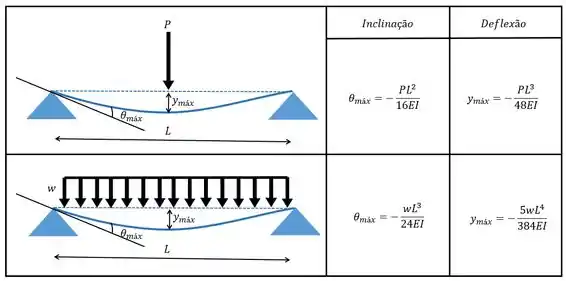
O nome dessa tabela é “Tabela de inclinações e deslocamentos” colocando no mestre Google a gente acha ela completa! Mas não precisa se preocupar, porque a pesar de não darmos a tabela completa vamos dar os valores nos exemplos enquanto formos fazendo, fechou?
Pessoal, a gente não quer o valor da inclinação no ponto central? Sim, queremos! E a tabela não dá esse valor, dá apenas o valor máximo (que ocorre na extremidade). E agora?
Gente, por causa da simetria da figura o ponto central vai ter inclinação nula!
Agora vamos calcular a deflexão, que vai ser a máxima, novamente pelo mesmo motivo de simetria!
Se a gente olhar só o primeiro caso, da força vamos ter que:
Então podemos dizer que:
E para o segundo caso vamos ter:
Logo,
O método da superposição diz que basta realizar a soma algébrica destes valores. Portanto vamos ter:
Pronto!! Viu como a utilização da tabela simplifica muito a nossa vida?
A gente não teve que fazer isso com o ângulo mas seria a mesma coisa! Só realizar a soma algébrica das inclinações de cada caso!
Caso especial
A gente tem que saber mais uma coisinha. Por mais que na tabela completa existam muitos casos nunca vamos conseguir ter todos, correto? Então vou apresentar um caso especial aqui para vocês. É o caso de uma viga em balanço:
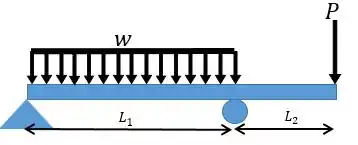
Neste caso vamos ter que dividir em três partes:
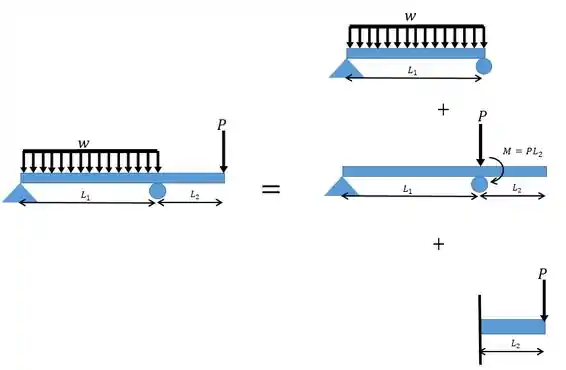
Reparem que a última parte nos consideramos como se estivesse engastada. Outro ponto importante é perceber que, no segundo caso, houve um deslocamento da força o que levou ao aparecimento de um momento .
Caso a dúvida sobre a possível contabilização dupla da força tenha surgido, não se preocupe porque no segundo caso a força é aplicada sobre o apoio e portanto não influencia nem na inclinação nem na deflexão.
É claro que existem infinitos casos, então para ficar craque que tal fazermos alguns exercícios??
Fazendo o cálculo
Caso especial
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine o deslocamento e a inclinação em . Considere constante.
Passo 1
Fala aí, pessoal!! Para resolver essa questão a gente só precisa ir na nossa tabela de inclinações e deflexões de vigas em balanço e achar o respectivo carregamento! É bem simples mesmo, vem comigo!
Passo 2
A nossa tabela nos fornece:
Como a tabela fornce os valores máximos e esses ocorrem na extremidade da viga (exatamente em ) então basta substituir.
Para a inclinação vamos ter:
E para a deflexão:
Ou podemos colocar os valores em módulo e indicar o sentido:
Para baixo.
Resposta
Ou podemos colocar os valores em módulo e indicar o sentido:
Para baixo.
Exercício Resolvido #2
Elaboração própria
Determine a inclinação e o deslocamento em . Considere constante.
Passo 1
Fala aí, pessoal!! Essa questão envolve dois carregamentos distintos então nós vamos ter que separá-los, achar a inclinação e deslocamento de cada um e depois é só somar os resultados.
Então vamos lá!
Passo 2
A nossa tabela nos fornece:
Como a tabela fornce os valores máximos e esses ocorrem na extremidade da viga (exatamente em ) então basta substituir.
Vamos fazer primeiro o carregamento uniforme:
Para a inclinação vamos ter:
E para a deflexão:
Passo 3
Agora vamos fazer para a força:
E para a deflexão:
Passo 4
Agora é só somar e para a inclinação vamos ter:
Para a deflexão:
Resposta
Ou podemos colocar os valores em módulo e indicar o sentido:
Para baixo.
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 455. Problema 12.89
A viga em balanço com perfil feita de aço é submetida à carga mostrada na figura. Determine o deslocamento em sua extremidade .
Passo 1
Fala aí, pessoal!! Para resolver essa questão utilizando o método da superposição dos efeitos a gente precisa fazer duas coisas basicamente.
- Dividir as duas cargas aplicadas na viga. Essas cargas são: a força de e o momento puro de .
- Calcular, por meio da tabelinha, a deflexão de cada carga e realizar a soma algébrica dessas deflexões.
Beleza? Vamos fazer isso aí então.
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
Pronto! Esse passo é bem simples não é mesmo? Só dividir cada carregamento em desenhos separados.
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão no ponto :
Pela tabela vamos ter que a deflexão causada pela força de será de:
Como e , vamos ter:
Agora para o momento puro:
Como e vamos ter:
obs: Reparem que utilizamos o comprimento de onde efetivamente o momento é aplicado, que é o ponto , mas não queremos no ponto queremos no ponto .
Logo, para resolver essa questão a gente tem que fazer o seguinte: Perceber que depois da carga a inclinação continua constante. Se a inclinação continua constante a deflexão varia linearmente. Assim a deflexão em , causada pelo momento, vai ser:
Faz sentido, não faz? Se a inclinação é constante, então a deflexão terá de ser o dobro quando também é dobrado!
Passo 4
Agora é só somar essas deflexões:
Agora só falta substituir e . Mas isso é tranquilo..
Como o aço é o então:
E como é um perfil então:
Substituindo na nossa equação:
Resposta
Ou
Para baixo
Exercício Resolvido #4
Elaboração própria
Determine o deslocamento e a inclinação em . Considere constante.
Passo 1
Fala aí, pessoal!! Para resolver essa questão a gente só precisa ir na nossa tabela de inclinações e deflexões de vigas em balanço e achar o respectivo carregamento!
Dessa vez a gente vai ver que esse carregamento triangular que é finalizado no meio da viga não existe na tabela. Então vamos utilizar ainda a tabela mas para saber o valor exato vamos aplicar também alguns conceitos de geometria, vem comigo!
Passo 2
A nossa tabela nos fornece:
Como dito anteriormente esse não é o carregamento exatamente igual ao do problema. Mas aí que vai entrar a geometria. Vamos olhar o nosso carregamento original:
Perceba que quando o carregamento cessa não há mais forças atuando na viga. Por esse motivo a inclinação da viga permanecerá constante. Assim se acharmos a inclinação da viga ao final do carregamento essa inclinação será a mesma em também!
Passo 3
Como a gente tem que a inclinação é constante, para achar a deflexão basta multiplicar a inclinação pela distância até a ponto . E temos de considerar também a deflexão máxima, que é somada a isso tudo.
Resposta
Podemos expressar em módulo indicando o sentido:
para baixo.
Exercício Resolvido #5
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 455. Problema 12.91
A viga simplesmente apoiada com perfil feita de aço é submetida à carga mostrada na figura. Determine a deflexão em seu centro .
Passo 1
Fala aí, pessoal!! Para resolver essa questão utilizando o método da superposição dos efeitos a gente precisa fazer duas coisas basicamente.
- Dividir as duas cargas aplicadas na viga. Essas cargas são: a carga distribuída de e o momento puro de .
- Calcular, por meio da tabelinha, a deflexão de cada carga e realizar a soma algébrica dessas deflexões.
Beleza? Vamos fazer isso aí então.
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
Pronto! Esse passo é bem simples não é mesmo? Só dividir cada carregamento em desenhos separados.
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão no ponto :
Como queremos no ponto que é o centro vamos ter que a deflexão causada pela carga distribuída vale:
Perceba que a tabela já nos fornece a deflexão no ponto médio. Desta forma não precisamos substituir na equação da curva, diferentemente do momento.
E para o momento puro:
Agora podemos substituir:
obs: Aqui é válido notar que tanto o momento do nosso problema quanto o momento da tabela geram deflexões negativas ok? Ambos estão no mesmo sentido.
Outra coisa legal de ver é que apesar de na tabela parecer que as cargas estão na outra extremidade da viga é só a gente olhar a viga pelo outro lado e verificar que as cargas na verdade são idênticas.
Passo 4
Agora é só somar essas deflexões:
Agora só falta substituir e . Mas isso é tranquilo..
Como o aço é o então:
E como é um perfil então:
Substituindo na nossa equação:
Ou
Para baixo
Resposta
Ou
Para baixo
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 456. Problema 12.98
A extremidade da haste está presa por um pino e acoplada a uma mola de torção de rigidez que mede o torque por radiano de rotação da mola. Se uma força for sempre aplicada perpendicularmente à extremidade da haste, determine o deslocamento da força
Passo 1
Galera, essa questão é bem parecida com as que a gente tem feito, a única diferença é que agora tem uma mola de torção. Mas isso não é problema porque podemos utilizar o método da superposição ainda.
Vamos fazer o seguinte, ver o quanto é a deflexão da força , pela tabela. Depois a gente vai somar essa deflexão com a deflexão que ocorreria se existisse apenas a mola!
Partiu resolver!
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
A deflexão causada pela mola pode ser calculada a partir da equação de uma mola de torção onde a torção é igual à constante vezes o ângulo:
Como o torque é igual à força vezes a distância:
Vamos ter que:
Logo a inclinação relativa à mola vai ser de:
Mas não queremos a inclinação, queremos a deflexão, então basta multiplicar pela distância .
Essa deflexão é para baixo!
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão por causa da força :
Assim vamos ter
Podemos escrever como um deslocamento positivo mas para baixo:
Passo 4
Agora é só somar essas deflexões:
para baixo.
Resposta
para baixo.
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 456. Problema 12.93
Determine o momento em termos da carga e a dimensão de modo que a deflexão no centro da viga seja nula. constante.
Passo 1
Faaala, galerinha!! Esse problema nos fornece um eixo com dois apoios e com uma força e dois momentos atuantes. Para resolver isso e achar o valor de e de forma que a deflexão no centro seja nula a gente vai fazer separadamente:
- A deflexão causada pela força .
- A deflexão causada pelos momentos .
A soma dessas deflexões deve ser zero. Importante lembrar que vamos fazer isso utilizando as tabelas.
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
Bem tranquilo né? Só separar cada carga em um desenho.
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão por causa da força :
Perceba que as partes externas do nosso eixo não influenciam agora então vamos olhar apenas a parte interna e a nossa equação é:
Substituindo os valores vamos ter:
Show! Essa é a deflexão causada pela força .
Passo 4
Agora vamos olhar a deflexão causada pelos momentos, mas não existe nenhuma tabela com a mesma configuração do nosso problema. O que temos é essa aqui:
Aí agora a gente tem que fazer uma sacação bolada para sair do que temos e chegar em algo parecido com isso aí! O que a gente tinha era o seguinte:
Nesse caso o momento fletor acaba sendo constante por todo o eixo e vale exatamente , logo podemos transformar o carregamento a cima em:
E pronto! Chegamos num desenho igual ao da tabela (lembre que os apoios aqui são de segundo gênero também). Temos que ver também que temos dois momentos ao invés de apenas um e que eles têm sentido oposto ao da tabela então deveremos mudar o sinal. Assim, vamos obter:
Como
Passo 5
Agora é só somar ambos os valores:
Referente à força:
Referente aos momentos:
Esse valor é aproximadamente
Resposta
Que é aproximadamente:
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 457. Problema 12.100
Determine a deflexão vertical e a inclinação na extremidade do suporte. Considere que ele está engastado na base e despreze a deformação axial do segmento . é constante.
Passo 1
E ai, pessoal!! Essa questão aqui é um pouquinho diferente né? Mas se liga, não é muito mais complicada não porque nós vamos analisar separadamente cada barra. Então vamos ter isso aqui ó:
Olha como ficou bem mais simples o problema né? Agora é só fazer cada um separadamente =D
Perceba que quando cortamos a barra a gente tem que introduzir um engaste para que a barra horizontal permanece em equilíbrio! Afinal as duas barras estavam realmente unidas não é mesmo?
Passo 2
Começando pela barra vertical a gente vai ter:
Utilizando a tabelinha:
Então podemos substituir os valores para achar a inclinação:
E para a e deflexão:
obs: Reparem que utilizei porque aqui a deflexão é na horizontal!
Passo 3
Agora vamos olhar o trecho horizontal:
Com a tabela vamos ter:
Assim a inclinação será dada por:
E a deflexão:
Passo 4
Agora nós temos de combinar esses valores. Normalmente a gente faria apenas uma soma normal, mas aqui nós temos duas barras diferentes.
Pessoal, a inclinação é mais fácil. É basicamente só somar a inclinação das duas barras. Mas aqui a gente tem que lembrar que o carregamento distribuído vai exercer um momento na barra vertical que não foi contabilizado. Assim devemos incluir uma inclinação , onde:
Logo, somando todos os termos vamos ter:
Para a deflexão:
