Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 126

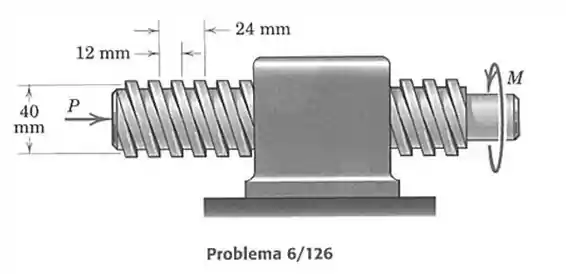
126- O parafuso com 40   m m de diâmetro tem uma rosca quadrada dupla com passo de 12   m m e avanço de 24   m m . O parafuso e as roscas correspondentes no bloco fixo são lubrificados com grafite e têm um coeficiente de atrito de 0.15 . Se um torque M = 60 N m é aplicado a parte direita do eixo, determine a ) a força P necessária para avançar o eixo para a direita e b ) a força P que permitiria que o eixo se movesse para a esquerda a velocidade constante.

Passo 1

Dados do parafuso:

Momento M : 60   N m

Avanço L : 24   m m (sempre usar o avanço por volta, as vezes eles são iguais mas nesse caso que tem rosca dupla não será)

Raio r : 40 2   m m = 20   m m

Ângulo de atrito ϕ :

ϕ = t g - 1   μ = t g - 1 0.15 = 8.53

Ângulo de hélice α :

α = t g - 1 L 2 π r = t g - 1 24 2 π × 20 = 10.81

Note que nesse caso α > ϕ , logo o parafuso irá se desparafusar por si mesmo, ou não é autotravante.

Passo 2

Letra a) Como o parafuso não é autotravante, isso nos diz que o parafuso será mais difícil de parafusar do que a média e como a força axial está da esquerda para a direita então o sentido de parafusamento está na mesma direção, logo o momento necessário para não deixar o parafuso se soltar será de:

M = F r tan ⁡ ( α - ϕ )

60 = F × 20 × 10 - 3   t a n ⁡ ( 10.81 - 8.53 )

Isso nos dará uma força de:

F = 75.35   k N

Passo 3

Letra b) Para desparafusar a força será bem menor, já que agora o parafuso estará se ajudando mais que o normal para isso, logo a fórmula nesse caso será:

M = F r   t a n ⁡ ( α + ϕ )

60 = F × 20 × 10 - 3   t a n ⁡ ( 10.81 + 8.53 )

O que nos dará uma força de:

F = 8.55   k N

Resposta

a )   75.35   k N

b )   8.55   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a força de retenção na placa A tiver de ser 2k N , determine o torque M que deverá ser aplicado ao parafuso para apertá-lo. O parafuso de rosca quadrada tem raio médio de 10m m e avanço de rosca de
Se a força de aperto necessária na placa A tiver de ser 50N , determine o torque M que deveráser aplicado ao punho do grampo “ C ” para apertá-lo contra a placa. O parafuso de rosca quadrada tem raio
O macaco consiste em um membro que possui um parafuso de rosca quadrada, com diâmetro médio de 12,5m m , avanço de rosca de 5m m e coeficiente de atrito estático u=0,4 . Determine o torque M que dever
Os três blocos de pedra possuem massas m A=300k g , m B=75k g e m c=250k g . Determine a menor força horizontal P que deverá ser aplicada ao bloco C a fim de movê-lo. O coeficiente de atrito estático
A cunha 10∘ é conduzida sob a roda acionada por mola, cujo suporte de apoio C é fixo. Determine o coeficiente mínimo de atrito estático μs para o qual a cunha permanecerá no lugar. Despreze todo o atr