Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 139
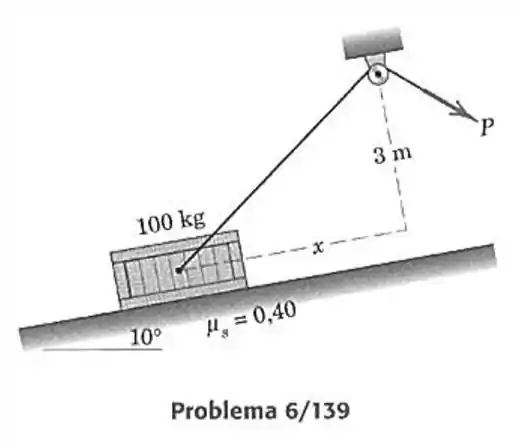
139- Faça um gráfico da força necessária para mover o caixote de para cima do plano com inclinação de , a partir do repouso, para vários valores de , desde zero até . Determine o menor valor possível de e o valor correspondendte de .
Passo 1
O peso do caixote é de:
Logo podemos montar o seguinte diagrama de corpo livre.
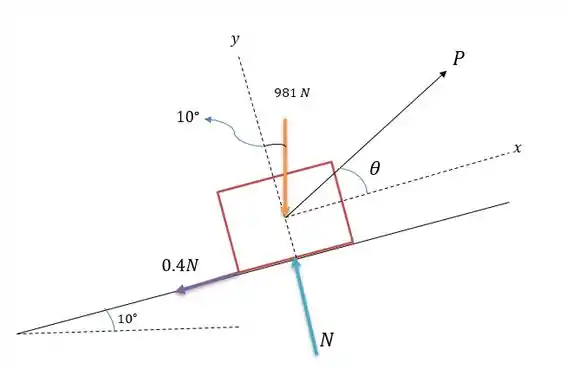
Onde precisamos estipular um ângulo que é formado entre a força e o bloco e uma força normal que será responsável por surgir a força de atrito igual a . Os eixos é normal ao plano.
Fazendo a somatória das forças em ser zero, temos:
Agora fazendo a somatória das forças em ser zero nós teremos:
Multiplicando a equação por e somando com a expressão nós iremos encontrar.
Passo 2
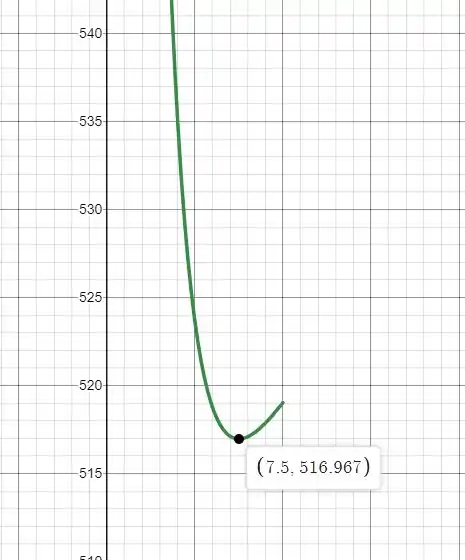
Agora para encontrar o menos valor possível de no intervalo dado basta derivar a equação de que encontramos e igualar ela a zero.
Pela regra do quociente.
Para essa equação ser zero a parcela precisa ser zero.
Esse ângulo nos dá uma força igual a:
Passo 3
Para encontrarmos o valor de nós devemos usar o triângulo retângulo abaixo:
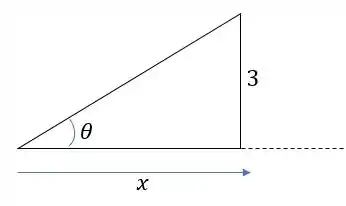
Fazendo a tangente de nós teremos:
Como encontramos para a menor força , nós teremos uma distância em:
Resposta
Gráfico de em relação a :
