Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 128

128- O carretel de cabo telefônico tem massa de 3   M g e se apóia em seu eixo sobre blocos em forma de V , dos dois lados do carretel. O carretel é erguido do solo elevando os suportes, de forma que o cabo pode ser puxado na direção horizontal, como mostrado. O eixo é preso ao carretel e gira junto com ele. Se o coeficiente de atrito entre o eixo e as superfícies em V vale 0.30 , calcule a força P no cabo necessária para girar o carretel.

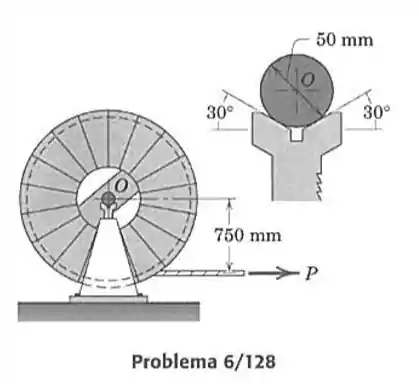
Passo 1

O apoio O é fixo logo a somatória das forças e dos momentos nesse ponto é nula, fazendo então o diagrama de forças em O temos:

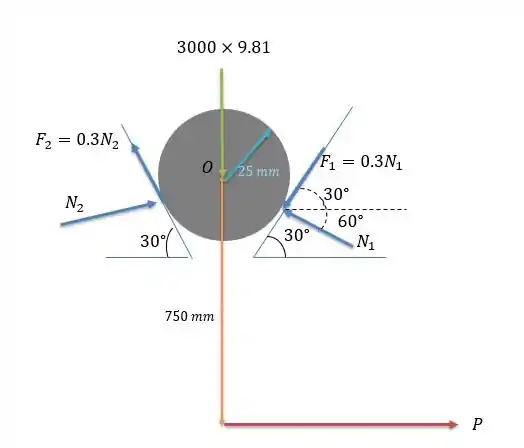
Como o carretel tende a girar no sentido anti-horário, logo as forças de atrito tendem a atuar no sentido horário.

E 3   M g = 3000   k g

Passo 2

Fazendo a somatória das forças horizontais nós teremos.

N 2 - N 1 cos ⁡ 60 - 0.3 N 2 + 0.3 N 1 cos ⁡ 30 + P = 0

0.24 N 2 - 0.76 N 1 = - P

Agora a somatória das forças verticais:

N 2 + N 1 sin ⁡ 60 + 0.3 N 2 - 0.3 N 1 sin ⁡ 30 - 3000 × 9.81 = 0

1.02 N 2 + 0.72 N 1 = 29430

Agora a somatória dos momentos em O :

- P × 0.75 + 0.3 N 1 + 0.3 N 2 × 0.0 2 5 = 0

Onde somente a força de atrito gera momento, pois ela sempre será perpendicular ao raio.

N 1 + N 2 = 100 P

Passo 3

Combinando a terceira equação com a primeira encontraremos:

0.24 N 2 - 0.76 N 1 = - P

0.76 N 1 + 0.76 N 2 = 76 P

N 2 = 75 P

Logo:

0.24 × 75 P - 0.76 N 1 = - P

- 0.76 N 1 = - 9.88 P → N 1 = 25 P

Substituindo esses resultados na segunda equação:

1.02 × 75 P + 0.72 × 25 P = 29430

94.5 P = 29430 → 311.13   N

Resposta

P = 311.13   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No problema 8.72 , a força de aperto de 4,5N foi obtida apertando-se a morsa. Determine o torque que deve ser aplicado ao parafuso para afrouxar a morsa.
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
Se a viga A D estiver carregada como mostra a figura, determine a força horizontal P que deverá ser aplicada ao calço a fim de que seja removido de sob a viga. Os coeficientes de atrito estático nas s
Se o coeficiente de atrito estático entre todas as superfícies de contato é u , determine a força P que deverá ser aplicada ao calço para levantar o bloco com um peso W.
O coeficiente de atrito estático entre os calços B e C é u=0,6 e entre as superfícies de contato B e A e C e D, u =0,4 . Se a mola estiver comprimida 200m m quando na posição mostrada, determine a men