Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 170
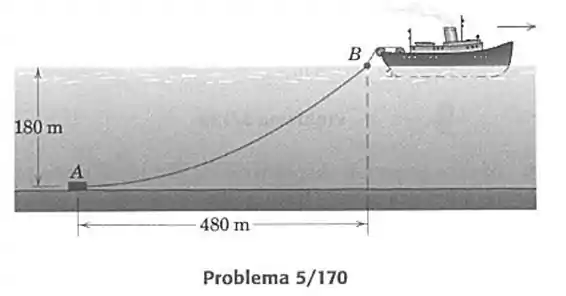
170- Um navio lançador de cabos submarinos reboca um equipamento para abrir valas , durante uma inspeção do leito submarino, para posterior colocação de um cabo telefônico. O navio mantém uma velocidade reduzida constante, com o equipamento em uma profundidade de e com um comprimento suficiente de cabo, de modo que o cabo sai horizontalmente do equipamento para abrir valas, o qual está atrás do navio. O cabo de reboque tem um peso efetivo de quando a flutuabilidade na água é levada em consideração. As forças sobre o cabo devido ao movimento através da água são desprezadas sob velocidade reduzida. Calcule a força horizontal aplicada ao equipamento de abrir valas e máxima força trativa no cabo. Ache, também, o comprimento do cabo de reboque do ponto até o ponto .
Passo 1
Como o cabo encontra-se na horizontal no ponto , logo podemos considerar o ponto como a origem da nossa equação da catenária. Com isso temos que o ponto encontra-se na posição de o que nos deixa com uma equação analítica nesse ponto igual a:
Numericamente nós encontraremos um valor de igual a:
Passo 2
Agora podemos encontrar a força de tração no ponto que será a maior força de tração no cabo.
Passo 3
O comprimento do cabo indo da origem até o ponto é dada por: