Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 43
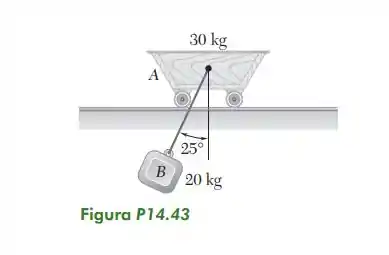
14.43. Um bloco B de 20 kg é suspenso por uma corda de 2 m fixada em um carrinho A de 30 kg, que pode rolar livremente sem atrito no caminho horizontal. Se o sistema é liberado do repouso na posição mostrada na figura, determine as velocidades de A e B quando B passa diretamente embaixo de A.
Passo 1
Vamos para mais uma questão!
Já de começo a gente pode dizer que o momento linear inicial do sistema é nulo, olha só, o sistema e liberado do repouso, o que significa que no começo do movimento o sistema estava em repouso, o que significa que a velocidade era nula, logo o momento linear também é nulo.
Mas sabemos que o momento linear é conservado nesse movimento, então
O que significa
A gente pode usar esse resultado para isolar
Passo 2
Mas ainda não respondemos nada. Vamos continuar o problema usando outra lei de conservação, a conservação de energia. No inicio do movimento a energia cinética é nula, mas atenção, esse sistema não possui somente energia cinética, também existe uma energia potencial associada a gravidade, nós poderíamos dizer que a energia potencial é nula no inicio do movimento também, mas é mais simples resolver o exercício se a energia cinética for nula no ponto mais baixo do bloco.
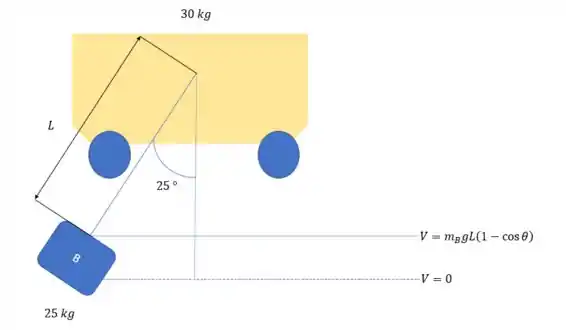
Vamos olhar direitinho como a gente define essa energia potencial. A equação para essa energia é .
Pela imagem a gente consegue ver melhor como calcular a altura do bloco.
E
Passo 3
Agora vamos usar a equação da conservação de energia.
Então
Olha só, a energia potencial assim que o bloco B está embaixo do carro A, a energia potencial é 0, como já definimos.
Passo 4
Vamos substituir nessa equação
Então isso vai ficar
Vamos multiplicar a equação por , e por em evidencia
Agora podemos achar uma equação para
Passo 5
Agora que temos a equação, é só substituir os valores, é só olhar o desenho da questão
E agora podemos descobrir o valor de
A gente deduziu essa equação lá no comecinho, lembra?