Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas de Revisão - Ex. 106

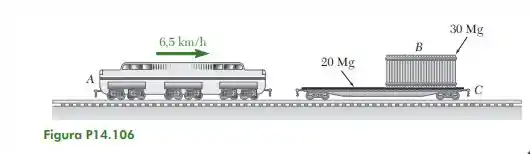
14.106. Uma locomotiva A de massa 80 Mg, movendo-se a uma velocidade de 6,5 km/h, atinge um vagão prancha C de 20 Mg que transporta uma carga B de 30 Mg, possível de deslizar sobre o piso do vagão ( μ k = 0,25 ) . Sabendo que o vagão estava em repouso com os freios liberados e que se engata automaticamente à locomotiva após o impacto, determine a velocidade do vagão (a) imediatamente após o impacto e (b) após a carga ter deslizado para uma nova posição de repouso em relação ao vagão.

Passo 1

A gente está quase acabando o capítulo!

A primeira coisa que a gente precisa é fazer as conversões de unidade. Para que nossas contas fiquem no SI temos que colocar todas as massas em k g e todas as velocidades em m s .

m A = 80   M g = 80 ⋅ 10 3 k g m B = 30   M g = 30 ⋅ 10 3 k g m C = 20   M g = 20 ⋅ 10 3 k g

E a velocidade

v A i = 6,5 k m h = 1,8 m s

Passo 2

Para resolver esse problema vamos usar conservação de momento linear.

∑ m i v i = ∑ m f v f

Assumindo que o momento final é o momento logo após o impacto

m A v A i = m A v f ' + m C v f '

Então

v f ' = m A v A i m A + m C

Substituindo os valores

v f ' = 80 ⋅ 10 3 1,8 80 ⋅ 10 3 + ( 20 ⋅ 10 3 ) = 1,4444 m s

Convertendo

v f ' = 1,4444 m s = 5,2 k m h

Passo 3

Agora vamos para o item (b). Depois que a carga desliza, a velocidade de todas as cargas é a mesma, então vamos fazer

m A v A i = m A + m B + m C v f

Então

v f = m A v A i m A + m B + m C

Substituindo os valores

v f = ( 80 ⋅ 10 3 ) ( 1,8 ) 80 ⋅ 10 3 + 30 ⋅ 10 3 + 20 ⋅ 10 3 = 1,1111 m s

Convertendo

v f = 4 k m h

Resposta

a : v f ' = 5,6 k m h                   b : v f = 4 k m h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As coordenadas retangulares de uma partícula são dadas em milímetros como funções do tempo t em segundos por x = 30 cos ⁡ ( 2 t ) , y = 40s e n ( 2 t ) e z = 20 t + 3 t 2 . Determine o ângulo θ 1 entr
Um robô industrial está sendo utilizado para posicionar uma pequena peça P . Calcule o módulo da aceleração a de P para o instante em que β = 30 ° se β ˙ = 10 graus por segundo e β ¨ = 20 graus por se
O carro A está subindo uma rampa de estacionamento na forma de uma hélice cilíndrica de raio 7,2m progredindo 3m para cada meia volta. Na posição mostrada o carro tem uma velocidade de 25k m / h , que
Uma aeronave decola em A e se eleva em um ângulo constante com inclinação de 1 para 2 no plano vertical y - z com uma velocidade constante v = 400k m / h . A aeronave é rastreada por radar em O . Para
O esguicho rotativo borrifa uma grande área circular e gira com a velocidade angular constante θ ˙ = K . Partículas de água deslocam-se ao longo do tubo em uma taxa constante l ˙ = c em relação ao tub