Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 221
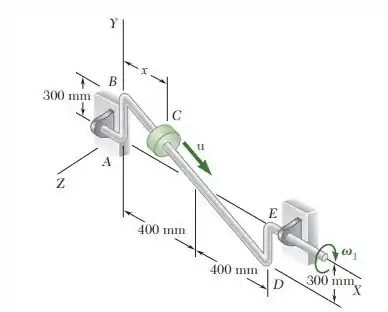
15.221. A barra dobrada mostrada na figura gira à taxa constante 1 3 rad /s. Sabendo que o colar C se desloca na direção do ponto D com uma velocidade relativa constante u 1 m/s, determine, para a posição mostrada na figura, a velocidade e aceleração de C se (a) x 100 mm, (b) x 400 mm.
Passo 1
Beleza, vamos lá!
Começando pelo item (a), temos
Agora nós podemos usar razão e proporção para determinar a altura do colar C. Repare bem que ele forma um triângulo.
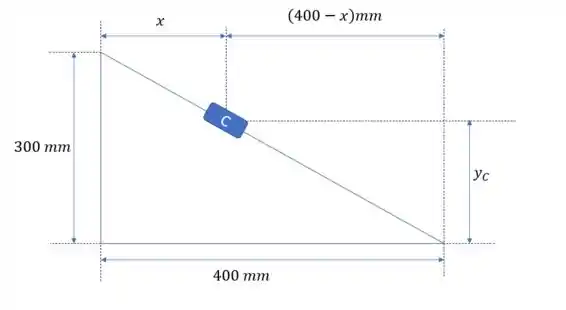
Para determinar só precisamos fazer
Então
E também podemos determinar um vetor unitário que aponta na direção de
Em que G é um ponto intermediário da barra .
Passo 2
Beleza, agora temos um vetor que aponta na direção da barra . Vamos começar a responder o item (a).
Bom, podemos calcular cada termo dessa soma separadamente.
Então temos que definir umas coisinhas aqui. Olhando a imagem podemos dizer que
E
Por tanto temos
E o outro termo
Do enunciado temos , então
Então
Passo 3
Agora vamos calcular a aceleração do colar C.
Temos aqui uma equação para ajudar a gente
Vamos resolver cada termo separadamente.
Mas é uma constante, isso implica que
Portanto
Isso fica
E o segundo termo
Esse foi fácil. E o ultimo termo
Isso fica
Então
Ou então
E assim temos nosso item (a) respondido.
Passo 4
Agora é a hora do item (b). .
Então
Então
Então agora temos
Vamos usar na equação
Isso fica
E da parte (a) podemos recuperar que
Isso não vai mudar.
Então da equação
Só nos resta
Logo
Passo 5
Vamos para a aceleração. Bom, como , então . E também sabemos do item (a) que . Então a equação
Se reduz a
E não vai se alterar, logo