Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 220

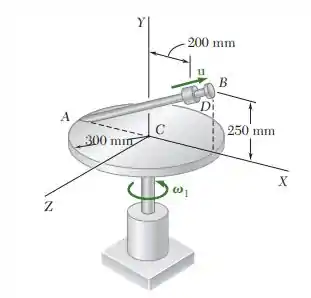
15.220. A barra AB está soldada em uma placa de 300 mm de raio que gira com uma taxa constante 1 6 rad /s. Sabendo que o colar D se desloca na direção da extremidade B da barra a uma velocidade constante u 2 m/s, determine, para a posição mostrada na figura, (a) a velocidade de D, (b) a aceleração de D.

Passo 1

Vamos começar esse problema aqui escrevendo umas informações importantes pra gente.

r → A B = 600   i ^ + 250   j ^ m m

Olha só, o segmento A D é uma parte do segmento A B . Aqui nós podemos usar razão e proporção para determinar o tamanho do segmento, como a gente pode ver na imagem, o colar D está a 200   m m do centro pelo eixo x , enquanto o ponto B está a 300   m m , que é exatamente o raio da circunferência, então temos que

r → A B = 300 300 r → A B

E

r → A D = 200 300 r → A B

Então

r → A D = 2 3 600   i ^ + 250   j ^   m m

Isso fica

r → A D = 400   i ^ + 166,167   j ^ m m

E também podemos usar o módulo de r → A B .

r → A B = r A B = 600 2 + 250 2 = 650   m m

A gente pode simplificar muito nossos cálculos se fizermos um vetor unitário que aponta na direção de r → A B , porque é exatamente a direção pela qual o colar D se move, então

u → A B = r → A B r A B

u → A B = 600   i ^ + 250   j ^ 650 = 12 13   i ^ + 5 13   j ^

Passo 2

Beleza, agora temos um vetor que aponta na direção da barra A B . Vamos começar a responder o item (a).

A velocidade de D é dada por

v → D = v → D ' + v D - A B

Onde

v → D ' = Ω → × r → C D

E

Ω → = ω → 1   j ^ = 6   j ^ r a d s

Também temos que usar

r → C D = r → A D - r → A C

Ou seja

r → D C = 400   i ^ + 166,167   j ^ - 300   i ^

r → D C = 100   i ^ + 166,167   j ^   m m

Então

v → D ' = 6   j ^ × 100   i ^ + 166,167   j ^  

Isso fica

v → D ' = - 600   k ^ m m s

E agora vamos nos concentrar no outro elemento da equação que vai nos dar a velocidade do colar D.

v D - A B = u ⋅ u → A B

Que vai ser a velocidade dada no enunciado na direção da barra AB.

u = 2 m s = 2000 m m s

v D - A B = 2000 ⋅ 12 13   i ^ + 5 13   j ^

E isso fica

v D - A B = 1846,15   i ^ + 792,23   j ^

E finalmente chegamos em

v → D = v → D ' + v D - A B

v → D = 1846,15   i ^ + 792,23   j ^ - 600   k ^ m m s

E essa é a resposta do item (a).

Passo 3

Agora vamos para o item (b), calcular a aceleração do colar D.

Temos aqui uma equação para ajudar a gente

a → D = a → D ' + a → D - A B + 2 Ω × v → D - A B

De novo vamos resolver cada termo separadamente.

a → D ' = - r ω 1 2   i ^

Isso fica

a → D ' = - 300 6 2   i ^ = 10800   i ^ m m s 2

E

a → D - A B = 0

Então só nos resta o termo

2 Ω × v → D - A B

Que fica

2 6   j ^ × 1846,15   i ^ + 792,23   j ^ = - 221538,8   k ^ m m s 2  

Então

a → D = 10800   i ^ - 221538,8   k ^ m m s 2

Ou

a → D = 10 , 8   i ^ - 221 , 5 4   k ^ m s 2

Resposta

a : v → D = 1846,15   i ^ + 792,23   j ^ - 600   k ^ m m s   b :   a → D = 10,8   i ^ - 221,54   k ^ m s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angula
O pino P desliza em uma ranhura circular cortada na placa mostrada na figura com uma velocidade relativa constante u = 90m m / s . Sabendo que, no instante mostrado, a velocidade angular ω da placa é
No instante mostrado na figura, a barra BC tem uma velocidade angular de 3r a d / s e uma aceleração de 2r a d / s 2 , ambas no sentido horário. Determine a aceleração angular da placa.
Sabendo que, no instante mostrado na figura, a barra articulada em B gira no sentido anti-horário com velocidade angular constante ω B de 6 rad /s, determine a velocidade angular e a aceleração angula
No instante mostrado na figura, a barra BC tem uma velocidade angular de 3r a d / s e uma aceleração de 2r a d / s 2 , ambas no sentido horário. Determine a aceleração angular da placa.